Received 12 May 2015; accepted 3 July 2015; published 6 July 2015

ABSTRACT

We stress a basic criterion that shows in a simple way how a sequence of real-valued functions can converge uniformly when it is more or less evident that the sequence converges uniformly away from a finite number of points of the closure of its domain. For functions of a real variable, unlike in most classical textbooks our criterion avoids the search of extrema (by differential calculus) of their general term.

Keywords:

Sequence of Functions, Uniform Convergence, Metric, Boundedness

1. Introduction

Let X be a nonempty set, be a function and be a sequence of real-valued functions from X into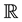. Recall [1] - [3] that the sequence 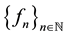is said to converge uniformly to f on X, if

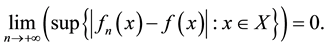
Obviously, if 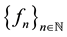converges uniformly to f on X, then for each 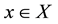fixed, the sequence 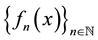converges to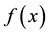; that is, 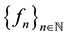converges pointwise to f. It is also obvious that when X is finite and 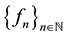converges pointwise to f on X, then 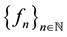converges uniformly to f on X. However this converse

doesn’t hold in general for an arbitrary (infinite) set X; i.e., the pointwise convergence may not imply the uniform convergence when X is an arbitrary (infinite) set.

One can observe that in the mathematical literature, there are very few known results that give conditions under which a pointwise convergence implies the uniform convergence. Concerning sequences of continuous functions defined on a compact set, we have the following facts:

Proposition A. (Dini’s Theorem) [4]

If K is a compact metric space, 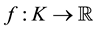a continuous function, and 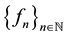a monotone sequence of continuous functions from K into 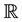that converges pointwise to f on K, then converges uniformly to f on K.

Proposition B. [5]

If E is a Banach space and is a sequence of bounded linear operators of E that converges pointwise to a bounded linear operator T of E, then for every compact set, converges uniformly to T on K.

(For the sake of completeness, we give the proof of this proposition in the Appendix Section).

Therefore our aim is to highlight a new basic criterion that shows in some way how a sequence of real-valued functions can converge uniformly when it is more or less obvious that the sequence converges uniformly away from a finite number of points of the closure of its domain. In the case of sequences of functions of a real variable, our criterion avoids, unlike in most classical textbooks [3] [6] , the search of extrema (by differential calculus) of their general terms. Several examples that satisfy the criterion are given.

2. The Main Result (Remark)

2.1. Theorem

Let be a metric space and be a subset of E. Consider a sequence of functions defined from to.

Suppose that there exists a function f from to, some points, some positive real numbers and a nonnegative constant M such that

(D)

Suppose furthermore that for each, converges uniformly to f on; where denotes the open ball of E centered at and with radius.

Then the sequence of functions converges uniformly to f on.

Proof

Let be arbitrarily fixed (it may be sufficiently small in order to be meaningful). Then for every natural number n, we have

Thus

by the uniform convergence of on.

And so

i.e.,

2.2. Observation

The boundedness condition (D) of the above theorem can not be removed as shown by the sequence of functions defined from into as follows:

where is equipped with its standard metric. Indeed, converges uniformly to 0 on for each, but with and there is no positive number r for which the condition (D) is satisfied since

And we can see that does not converge uniformly to 0 on since

3. Examples

We give some examples that illustrate the theorem.

(1) Let be an infinite metric space and let be fixed. Denote by the function defined from E into by

Then the sequence of functions defined by

converges uniformly to on E.

(2) Given an infinite metric space, and, we have that

i) the sequence of functions defined by

converges uniformly to 0 on E,

ii) the sequence of functions defined by

converges uniformly to 0 on E.

(3) Let be an infinite metric space and be a bounded and infinite subset of E, let a and b be two different points of and let and be two fixed positive numbers.

i) Consider the sequence of functions defined by

Then converges uniformly to 0 on.

ii) Consider the sequence of functions defined by

Then converges uniformly to 0 on.

iii) Consider the sequence of functions defined by

Then converges uniformly to 0 on.

(4) In real analysis, we can recover the facts that each of the following sequences converges uniformly to 0 on their respective domains:

Justifications (Proofs) of the examples

(1) For every, we have

Therefore, on the one hand, for each, we have

showing that converges uniformly to on.

On the other hand, we have

fulfilling condition (D) of the above theorem.

Thus converges uniformly to on E.

(2) i) On the one hand, for each, we have for all and for all with:

and so converges uniformly to 0 on.

On the other hand, we have

fulfilling condition (D) of the above theorem.

Thus converges uniformly to 0 on E.

ii) The uniform convergence of, follows that of since

Observe that the uniform convergence of could also be proved using directly the above theorem.

(3) Note that for all natural number n, we have

because

following from

Therefore it suffices to prove that converges uniformly to 0 on, although each of these three sequences can be handled directly with the above theorem.

Let be the diameter of.

Then on the one hand, for each, we have for all and for all:

and so converges uniformly to 0 on.

On the other hand, we have

showing condition (D) of the above theorem.

Thus converges uniformly to 0 on and we are done.

(4) i) Let us set with.

On the one hand, we have for every:

On the other hand, we have for every:

showing that converges uniformly to 0 on.

Therefore, by taking, , , , and, the above theorem implies that converges uniformly to 0 on.

ii) For with.

On the one hand, we have for every:

On the other hand, we have for every:

showing that converges uniformly to 0 on.

Therefore, by taking, , , , and, the above theorem implies that converges uniformly to 0 on.

iii) For with.

On the one hand, we have for every:

On the other hand, we have for every:

showing that converges uniformly to 0 on since.

Therefore, by taking, , , , and, the above theorem implies that converges uniformly to 0 on.

iv) For with.

On the one hand, we have for every:

On the other hand, we have for every:

showing that converges uniformly to 0 on since.

Therefore, by taking, , , , and, the above theorem implies that converges uniformly to 0 on.

v) The example of with, is a particular case of Example (2)-ii) above with, for all, and.

Cite this paper

GuyDegla,11, (2015) A Remark on the Uniform Convergence of Some Sequences of Functions. Advances in Pure Mathematics,05,527-533. doi: 10.4236/apm.2015.59048

References

Appendix

In this section, we prove Proposition B for the sake of completeness.

Proof of Proposition B

Let be given. By the Uniform Boundedness Principle, we have that. So let. Then there exist such that.

Also,. We have that

It follows that and therefore