International Journal of Nonferrous Metallurgy
Vol.04 No.01(2015), Article ID:53226,7 pages
10.4236/ijnm.2015.41001
A Fuzzy Logic Model to Predict the Bioleaching Efficiency of Copper Concentrates in Stirred Tank Reactors
Ali Ahmadi, Mohammad Raouf Hosseini
Department of Mining Engineering, Isfahan University of Technology, Isfahan, Iran
Email: a.ahmadi@cc.iut.ac.ir
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 December 2014; accepted 5 January 2015; published 14 January 2015
ABSTRACT
Multiplicity of the chemical, biological, electrochemical and operational variables and nonlinear behavior of metal extraction in bioleaching environments complicate the mathematical modeling of these systems. This research was done to predict copper and iron recovery from a copper flotation concentrate in a stirred tank bioreactor using a fuzzy logic model. Experiments were carried out in the presence of a mixed culture of mesophilic bacteria at 35˚C, and a mixed culture of moderately thermophilic bacteria at 50˚C. Input variables were method of operation (bioleaching or electrobioleaching), the type of bacteria and time (day), while the recoveries of copper and iron were the outputs. A relationship was developed between stated inputs and the outputs by means of “if-then” rules. The resulting fuzzy model showed a satisfactory prediction of the copper and iron extraction and had a good correlation of experimental data with R-squared more than 0.97. The results of this study suggested that fuzzy logic provided a powerful and reliable tool for predicting the nonlinear and time variant bioleaching processes.
Keywords:
Fuzzy Logic, Modeling, Copper Concentrate, Bioleaching, Stirred Reactor

1. Introduction
Conventional or electrochemical bioleaching of copper from concentrates in stirred tank reactors is one of the most complex and difficult processes in hydrometallurgy. It not only is nonlinear and time variant, but also is hardly defined. The bioleaching process has been constituted of two interacting subsystems: an abiotic system, which is a mineral suspension in a solution of chemical and electrochemical compounds and gases as well as a biological system, composed of a singular or mixed culture of microorganisms. For mathematical modeling of this process, mass transfer between three different phases that is too complicated, must be taken into account [1] . On the other hand, the presence of several species of acidophilic bacteria, which have different mechanisms to dissolve minerals (contacting and non-contacting mechanisms), has complicated the nature of the biological subsystem. So the system not only is difficult to formulate mathematically, but also is even more difficult to validate experimentally due to oversimplifications of the conditions, as a consequence, the process cannot be programmed in a precise way.
The use of fuzzy logic, which reflects the qualitative and inaccurate nature of human reasoning, can enable expert systems to be more flexible [2] . It was initiated in 1965 by Lotfi A. Zadeh [3] . In a fuzzy logic model, language terms (linguistic variables) are used to convey concepts relating to the system’s components and language instruments (linguistic operators) are used to convey concepts relating to the interrelationship and dynamics of these components. Fuzzy logic systems are widely used for control, system identification, and pattern recognition problems. The main advantage of fuzzy interference with respect to traditional mathematical models lies in the fact that the relationship between inputs and outputs is not determined by complex equations, but by a set of logical rules, reflecting an expert’s knowledge [4] . In complicated process control systems, fuzzy logic is integrated with conventional PID (proportional-integral-derivative) systems and is a very useful approach in pro- cess automation [5] . Fuzzy logic can be used in order to conveniently incorporate the practical in-house operating knowledge into the control solution [6] . During the last decade, researchers have attempted to predict both physical and chemical processing of ores and concentrates using fuzzy logic systems [5] [7] -[10] . Bioleaching process has also been modeled by different methods [11] -[15] . Pazuki et al. [16] used Artificial Neural Network to optimize the bioleaching of iron from a Kaolin ore, and a good agreement was obtained between the model and experimental data. A reaction-based kinetic model for conventional and electrochemical bioleaching of copper concentrates was previously published [13] .
Considering, the multiplicity of various chemical, biological, electrochemical and operational parameters, nonlinear behavior of metal extraction in bioleaching processes, and the high ability of knowledge based systems in such complex media, in this research, a multi input-multi output fuzzy logic model was defined to predict copper and iron recovery from a flotation copper concentrate in a stirred electro-bioreactor. The proposed model predicts the nonlinear behavior of conventional and electrochemical bioleaching processes successfully.
2. Experimental Data
Data used in this fuzzy logic modeling was obtained from an experimental work performed previously by the author and his coworkers [17] . In that research, a chalcopyrite copper concentrate from the Sarcheshmeh Copper Mine (Kerman, Iran) was used to perform conventional and electrochemical bioleaching processes. X-ray fluorescence (XRF) and X-ray diffraction (XRD) analyses of the sample showed 27.7% Cu, 24.6% Fe, 14.8% S, and chalcopyrite (CuFeS2) as the major mineral and pyrite (FeS2) as the minor one. Experiments were carried out in a three compartment electro-bioreactor at 10% (w/v) solid content. A mixed culture of mesophilic bacteria and a mixed culture of moderately thermophilic bacteria were used at 35˚C and 50˚C, respectively. Experiments were conducted in nutrient medium, 9 K; stirring rate, 450 rpm; applied potential, 420 mV (in electrobioleaching tests); initial pH, 1.8; and aeration rate, 1.3 L∙min−1. The potential of the working electrode was controlled with respect to the reference electrode using a Solartron Sl 1287 potentiostat. The details of apparatus and techniques used have been previously described [17] .
3. Fuzzy Logic Modelling
3.1. Modeling Structure
A fuzzy logic system is a nonlinear mapping of an input data (feature) vector into a scalar output [18] . It contains four components: fuzzifier, rules, inference engine, and defuzzifier. In this research, the fuzzy modeling process was supported by Fuzzy Logic Toolbox of the Matlab software (version 7.4.0). The standard method of creating the model can be seen in Figure 1.
3.2. Fuzzification of Variables
Fuzzification is the process of finding the membership degrees. A membership function (MF) is a curve that
Figure 1. The fuzzy logic modeling process.
defines how each point in the input space is mapped to a membership value (or degree of membership) between 0 and 1 (Fuzzy Logic Toolbox). The value 0 represents a complete non-membership, the value 1 represents a complete membership function and values in between are used to represent partial membership. The input and output variables have been fuzzified according to the linguistic sets shown in Table 1. Experimental results and expert knowledge was used to obtain the numbers of the input membership functions and base widths. As can be seen from Figures 2-4 triangular membership functions (Equation (1)) was used to make the input variable time and output variables copper and iron recovery. Each membership function has 30% - 60% overlap with the adjacent ones.
Ordinary (crisp) sets are a special case of fuzzy sets, in which the membership function only takes two values: 0 (non-membership) and 1 (membership) [19] . By considering this note, the input variables of “Method” and type of bacteria or “TOB” was defined as crisp sets which then was fuzzified in accordance with Equations (2) and (3). For “Method” variable, when the membership function is between 0 and 0.5, the bioleaching method (BL) is chosen and when it is between 0.5 and 1, the electrobioleaching method (EBL) is chosen. For “TOB” variable when the membership function is between 0 and 0.5, the mesophilic bacteria (M) are chosen and when it is between 0.5 and 1, the moderately thermophilic bacteria are chosen.
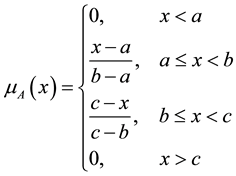 (1)
(1)
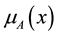 is the membership function of a fuzzy set; a, b, c are the constant.
is the membership function of a fuzzy set; a, b, c are the constant.
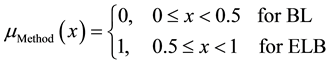 (2)
(2)
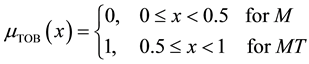 (3)
(3)
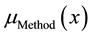 and
and 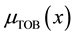 are the membership function of “Method” and “TOB” variables.
are the membership function of “Method” and “TOB” variables.
3.3. Fuzzy Rule Base and Logical Operators
Fuzzy rules could be derived from both expert’s reasoning and linguistic expressions and from the relationships between the system variables. To model the process, a fuzzy rule-based system was constructed with the 34 fuzzy if-then rules (Table 2). The relationships show some of the defined rules of the Mamdani fuzzy rule based system. Rules in the base contain fuzzy AND in antecedent part. To model the logical operator AND, one can use the main operator which gives the minimum membership degrees between two fuzzy sets of elements.
Table 1. Linguistic expressions used in input and output variables.
Table 2. Fuzzy rules for copper and iron recovery (TOB: type of bacteria; BL: bioleaching; ELB: electrobioleaching; MES: mesophilic bacteria; MT: moderately thermophilic bacteria).
Figure 2. Fuzzy logic membership functions for time variable (input).
Figure 3. Fuzzy logic membership functions for Cu recovery (response variable).
Figure 4. Fuzzy logic membership functions for Fe recovery (response variable).
Interpreting fuzzy AND as the minimum, one can rewrite rules as the form that is more concise:
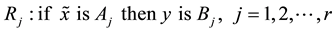 (4)
(4)
where 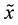 contains input variables as
contains input variables as  and
and 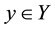 is the output variable, and:
is the output variable, and:

Each rule corresponds to a fuzzy relation given by Equation (6):

3.4. Fuzzy Inference
The fuzzy inference engine is the core of a fuzzy system. It is used to simulate the thinking and decision-making modes of human beings to solve problems [4] .
Having translated each rule 




3.5. Defuzzification
The process of reducing final obtained fuzzy set is termed defuzzification that converts the output fuzzy set that is inferred from the fuzzy inference engine to an ordinary value in 

where 
3.6. Model Validation
Modeling of complex and nonlinear copper bioleaching behavior (conventional and electrochemical) was done by a fuzzy logic model. A knowledge base containing if-then rules was developed in a natural language to store a human expert’s experience.
Variation of copper and iron recovery during electrobioleaching and bioleaching processes using both mixed mesophilic bacteria and mixed moderately thermophilic bacteria have been shown in Figure 5 and Figure 6. The figures show that the fuzzy logic model developed can predict the values of copper and iron recovery when proper input data (Method, TOB and Time) were entered. They clearly indicate that the recovery can be predicted very well with the fuzzy model in which R-squared of the model is more than 0.99 in all cases.
From Figure 5 and Figure 6, it can be seen that the fuzzy logic model can predict the recoveries at very small and very large values and the model considers the well nonlinear behavior of copper and iron extraction in different conditions. The fuzzy model could also be as a powerful tool for using in a control system on a stirred electro-bioreactor, provided a complete fuzzy knowledge base is formed on the basis of human experts’ experiences and real data obtained from experiments.
4. Conclusion
A fuzzy logic model was obtained to predict the recoveries of copper and iron from a chalcopyrite copper
Figure 5. Comparison of copper recovery data obtained from the experiments and the fuzzy model during bioleaching and electrobioleaching in a stirred bioreactor (BL: bioleaching; ELB: electrobioleaching).
Figure 6. Comparison of iron recovery data obtained from the experiments and the fuzzy model during bioleaching and electrobioleaching in a stirred bioreactor (BL: bioleaching; ELB: electrobioleaching).
concentrate by conventional and electrochemical bioleaching processes. The recoveries of these metals are targeted functions for hydrometallurgical extraction of copper from copper flotation concentrates. The input variables were the method of process (bioleaching or electrobioleaching), the type of bacteria (mesophilic and moderately thermophilic bacteria) and time (day). A fuzzy relationship was developed between stated inputs and the outputs by means of “if-then” rules. The comparison of the experimental data and predicted values of the model showed a good match between them, in which the R-squared of the model was more than 0.97 in each series of data. The results showed the capability of the fuzzy model to flexibly predict complex and nonlinear bioleaching processes and it is a powerful tool for metal extraction in such a complicated system.
Acknowledgements
The authors would like to thank the National Iranian Copper Industry Company (NICICO) that allowed them to use experimental data for conducting this research.
References
- Rossi, G. (1990) Biohydrometallurgy. McGraw-Hill, Boston.
- Pham, D. and Pham, P. (1999) Artificial Intelligence in Engineering. International Journal of Machine Tools and Manufacture, 39, 937-949. http://dx.doi.org/10.1016/S0890-6955(98)00076-5
- Zadeh, L.A. (1965) Fuzzy Sets. Information and Control, 8, 338-353. http://dx.doi.org/10.1016/S0019-9958(65)90241-X
- Hsiang, S. and Lin, Y. (2008) Application of Fuzzy Theory to Predict Deformation Behaviors of Magnesium Alloy Sheets under Hot Extrusion. Journal of Materials Processing Technology, 201, 138-144. http://dx.doi.org/10.1016/j.jmatprotec.2007.11.222
- Bergh, L., Yianatos, J. and Leiva, C. (1998) Fuzzy Supervisory Control of Flotation Columns. Minerals Engineering, 11, 739-748. http://dx.doi.org/10.1016/S0892-6875(98)00059-4
- http://www.outotec.com/en/Products--services/Analyzers-and-automation/Zinc-refining-control-solutions/
- Abou, S.C. and Dao, T.-M. (2009) Fuzzy Logic Controller Based on Association Rules Mining: Application to Mineral Processing. Proceedings of the World Congress on Engineering and Computer Science, 2.
- Carvalho, M.T. and Durão, F. (2002) Control of a Flotation Column Using Fuzzy Logic Inference. Fuzzy Sets and Systems, 125, 121-133. http://dx.doi.org/10.1016/S0165-0114(01)00048-3
- Vieira, S., Sousa, J. and Durao, F. (2005) Fuzzy Modelling Strategies Applied to a Column Flotation Process. Minerals Engineering, 18, 725-729. http://dx.doi.org/10.1016/j.mineng.2004.10.008
- Saravani, A., Mehrshad, N. and Massinaei, M. (2014) Fuzzy-Based Modeling and Control of an Industrial Flotation Column. Chemical Engineering Communications, 201, 896-908. http://dx.doi.org/10.1080/00986445.2013.790815
- Petersen, J. and Dixon, D. (2007) Modelling Zinc Heap Bioleaching. Hydrometallurgy, 85, 127-143. http://dx.doi.org/10.1016/j.hydromet.2006.09.001
- Bennett, C., McBride, D., Cross, M. and Gebhardt, J. (2012) A Comprehensive Model for Copper Sulphide Heap Leaching: Part 1 Basic Formulation and Validation Through Column Test Simulation. Hydrometallurgy, 127, 150-161. http://dx.doi.org/10.1016/j.hydromet.2012.08.004
- Ahmadi, A., Ranjbar, M., Schaffie, M. and Petersen, J. (2012) Kinetic Modeling of Bioleaching of Copper Sulfide Concentrates in Conventional and Electrochemically Controlled Systems. Hydrometallurgy, 127, 16-23. http://dx.doi.org/10.1016/j.hydromet.2012.06.010
- Leahy, M.J., Davidson, M.R. and Schwarz, M.P. (2005) A Two-Dimensional CFD Model for Heap Bioleaching of Chalcocite. ANZIAM Journal, 46, C439-C457.
- Gonzalez, R., Gentina, J.C. and Acevedo, F. (2004) Biooxidation of a Gold Concentrate in a Continuous Stirred Tank Reactor: Mathematical Model and Optimal Configuration. Biochemical Engineering Journal, 19, 33-42. http://dx.doi.org/10.1016/j.bej.2003.09.007
- Pazouki, M., Ganjkhanlou, Y., Tofigh, A., Hosseini, M., Aghaie, E. and Ranjbar, M. (2012) Optimizing of Iron Bioleaching from a Contaminated Kaolin Clay by the Use of Artificial Neural Network. International Journal of Engineering-Transactions B: Applications, 25, 81-88.
- Ahmadi, A., Schaffie, M., Manafi, Z. and Ranjbar, M. (2010) Electrochemical Bioleaching of High Grade Chalcopyrite Flotation Concentrates in a Stirred Bioreactor. Hydrometallurgy, 104, 99-105. http://dx.doi.org/10.1016/j.hydromet.2010.05.001
- Mendel, J.M. (1995) Fuzzy Logic Systems for Engineering: A Tutorial. Proceedings of the IEEE, 83, 345-377. http://dx.doi.org/10.1109/5.364485
- Kasabov, N.K. (1996) Foundations of Neural Networks, Fuzzy Systems, and Knowledge Engineering. Marcel Alencar, New York.
- Nguyen, H.T., Prasad, N.R., Walker, C.L. and Walker, E.A. (2010) A First Course in Fuzzy and Neural Control. CRC Press, Boca Raton.
- Nguyen, H.T. and Walker, E.A. (2005) A First Course in Fuzzy Logic. CRC Press, Boca Raton.








