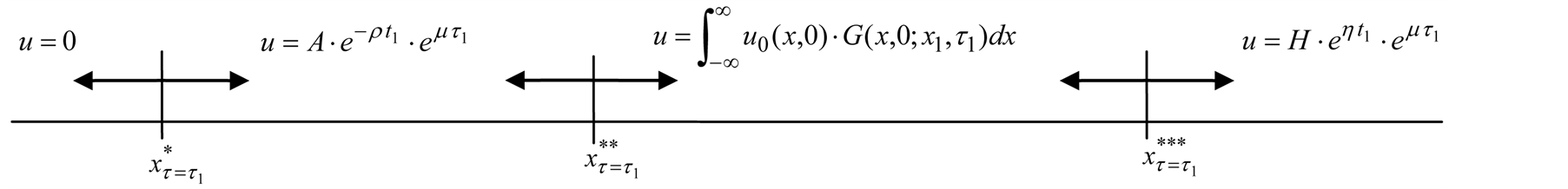Journal of Mathematical Finance
Vol.04 No.05(2014), Article ID:51559,8 pages
10.4236/jmf.2014.45028
The Project Valuation with Abandonment and Reset Investment Proportion Applying Real Option Method
Yi-Long Hsiao1, Li-Ling Chen2
1Department of Finance, National Cheng Kung University, Taiwan
2Department of Food and Beverage Management, Tatung Institute of Technology, Taiwan
Email: hsiao@mail.ndhu.edu.tw, judychen@ms2.ttc.edu.tw
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 August 2014; revised 8 September 2014; accepted 23 September 2014
ABSTRACT
We discuss the valuation of investment project in a firm applying a real option method with abandonment and reset investment proportion. We take the depreciation value of the facilities and the research and development (R & D) fee into consideration. Our contribution is to derive a pricing model of two-stage optimal decisions allowing abandonment and reset investment proposition. Different from the net present value (NPV) or discount cash flow (DCF), the real option method can efficiently catch the uncertainty in the market, and it can help managers to make the optimal policy for the project. We can improve our method for a multi-stage decision model or a continuous decision model in the further researches.
Keywords:
Real Option, Project Valuation, Two-Stage Decision

1. Introduction
We discuss the valuation of investment project in a firm applying a real option model with abandonment and reset investment proportion. We take the depreciation value of the facilities and the research and development (R & D) fee into consideration. Because of the uncertainty of the real world, the policy-making of a firm should be dynamic. We focus on deriving a pricing model of two-stage optimal decisions allowing abandonment and reset investment proposition in this study.
The traditional method to evaluate a project is through the net present value (NPV) or discount cash flow (DCF). If the net present value of the project is positive after considering the future cash flow of each period, we would accept the project. Otherwise we will decline it. Robichek and Horne [1] first suggested that if the residual value of a project was greater than the present value of the operating cash flow, the managers would cease the project. However, Dyl and Long [2] reported that allowing abandonment of a project would delay to exercise the abandonment options because of different residual values of the project or policy-making points. Therefore, the strategy of Robichek and Horne [1] may not be optimal for the project at the decision point. Hayes and Garvin [3] proposed that using NPV to evaluate a project would undervalue or miss the opportunity value of the investments, so the managers could not make the optimal policy to the project immediately during a short time when the transient investment opportunity appeared. The scope of a project would expand or shrink according to each situation in the real world. Nevertheless, NPV and DCF can’t catch the expected uncertainty in the market, and they are hard to evaluate the approximate value of the project in a firm. The advantage of our model is that we can extend or reduce the investment proportion of a project according to situations in the market with time.
Because of the maturation of appropriate valuation models in barrier options and reset options recently, we could apply the concepts of barrier options and reset options to evaluate a project and derive the valuation of two-stage decision model, which can extend or reduce the scope of a project in the policy-making point. We could further study which models are more compatible with the real world—multi-stage decisions models or continuous decisions models.
The rest of this paper is organized as follows. Section 2 is the literature review. Section 3 is the methodology about considering only abandonment, or both abandonment and reset investment proportion. Finally, Section 4 discusses the conclusions and recommendations of further researches.
2. Literature Review
Robichek and Horne [1] first suggested that if the residual value of a project is greater than the present value of the operating cash flow, the managers will cease the project. However, Dyl and Long [2] reported that allowing abandonment of a project in different residual values or time points would delay to exercise abandonment options. Hayes and Garvin [3] proposed that using NPV to evaluate a project would undervalue or miss the opportunity value of the investments, so the managers cannot make an optimal policy to the project immediately during a short time when the transient investment opportunity appears.
Since Gray and Whaley [4] and Boyle and Lau [5] developed the valuations of reset put options and barrier options respectively, merchandise bound up with those are very famous in the financial market as hedging or speculating instruments. Cheng and Zhang [6] proposed closed form solutions of the discrete multi-stage reset option represented as a multiple variables normal distribution. Boyle, Kolkiewicz and Tan [7] used Monte Carlo Simulation to price reset options. Kimura and Shinohara [8] discovered that convertible bonds generally have reset conditions additionally. Furthermore, Ritchken [9] used a stretch parameter and trinormal lattice model to increase the probability of barrier level near the nodes. Broadie, Glassman and Kou [10] and Hörfelt [11] derived the formula of discrete single barrier option. Ahn, Figlewski and Gao [12] used an adaptive mesh model to price discrete barrier option. Hence, the valuations of reset options and barrier options are very mature and popular.
We focus on applying the concepts of reset options and barrier options to the valuation of a project in a firm. We derive the valuation of two-stage decision model, and we put more emphasis on the research and development (R & D) fee into consideration. We could derive a general valuation model in the future researches.
3. Methodology
This paper discusses the two-stage decisions of a project in a firm using the valuation of real options with abandonment and reset conditions. The valuation is a series of initial value problems because of discrete policy- makings in multi-stage time. According to different criterions at different policy-making points, it is a series of free boundary problems. Therefore, the valuation of the decision problem can be viewed as a series of combinations of initial value problems and free boundary value problems. We adapt an approach to solve a partial differential equation (PDE)—Green’s function, which is useful to solve the initial value problem and boundary value problem, to discuss the valuation of a project in a firm.
3.1. Basic Assumption
We adapt the fundamental assumptions in Kulatilaka and Perotti [13] as following two points.
1) We assume that the demand of the goods is linear in prices and increases with a random variable , then the inverse demand function,
, then the inverse demand function,  , represents the market price as follows:
, represents the market price as follows:
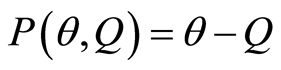
where Q is the total supply in the market, and the random variable  satisfies the geometric Brown motion with expected return
satisfies the geometric Brown motion with expected return 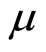 and volatility
and volatility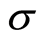 .
.
2) If no initial investment is made, the firm will produce only when the market is profitable with a unit cost of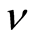 . The function of production benefit of the firm can be defined as
. The function of production benefit of the firm can be defined as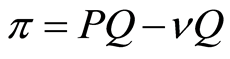 . When the production
. When the production
quality Q reaches the balance 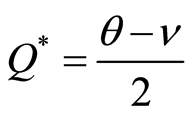 in the market, the maximum benefit of production is
in the market, the maximum benefit of production is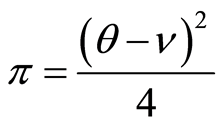 .
.
Next, we define A to be a part of the project asset which can be sold in the market, such as the real estate, facilities or factory buildings. Suppose the average depreciation rate of facilities is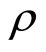 . The firm can decide to cease the project in the maturity date T and sell the asset A to the market with the depreciation value,
. The firm can decide to cease the project in the maturity date T and sell the asset A to the market with the depreciation value,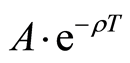 . In addition, the part of asset which cannot be sold is N, such as salary, research and development (R & D) fee. Suppose the natural growth rate of the research and development (R & D) fee is
. In addition, the part of asset which cannot be sold is N, such as salary, research and development (R & D) fee. Suppose the natural growth rate of the research and development (R & D) fee is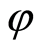 , then the fee at the maturity date T is
, then the fee at the maturity date T is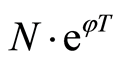 .
.
Furthermore, we suppose that the products have a maximum demand in the real market, and the facilities of the project have finite ability to produce the products. We consider the present maximum balance benefit is H, and it increases with time by the natural growth rate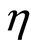 . The maximum balance benefit at the maturity date T will be
. The maximum balance benefit at the maturity date T will be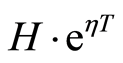 .
.
3.2. The Payoff of Real Option with Abandonment at Maturity T
When the maximum benefit of production 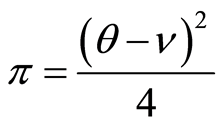
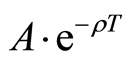
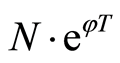
efit of production 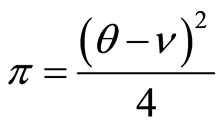

cient to pay the increasing research and development (R & D) fee 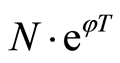

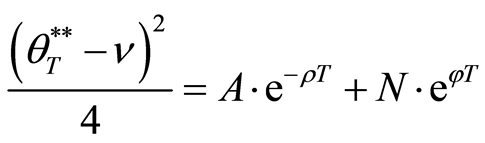
where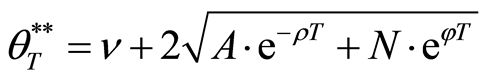
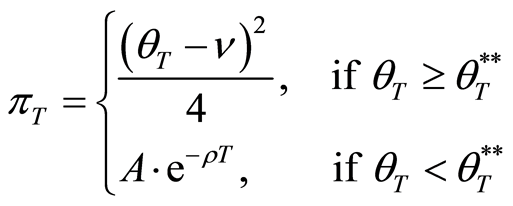
where 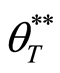
In addition, other firms would buy the old facilities of the project only if the benefit is greater than the cost they pay. On the contrary, if the benefit which the facilities would create is lesser than the cost of the facilities, there will be no firm buying the facilities. The project will be worthless. Therefore, the balance point will satisfy the following equation:
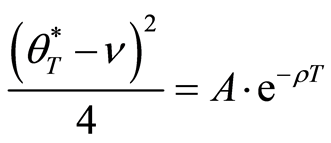
where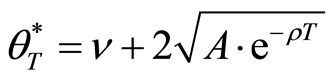
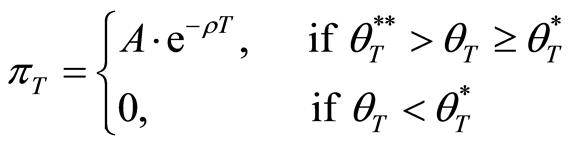
where 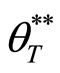
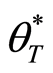
When we continue to produce the products, we can obtain more benefit. However, there is a maximum balance benefit at each policy-making point after considering the demand of population and the ability of the facilities. It means that the benefit is finite. Therefore, the threshold 
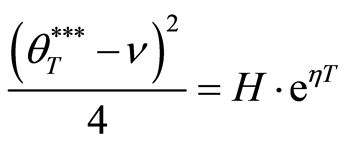
where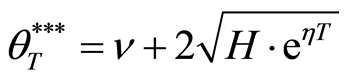
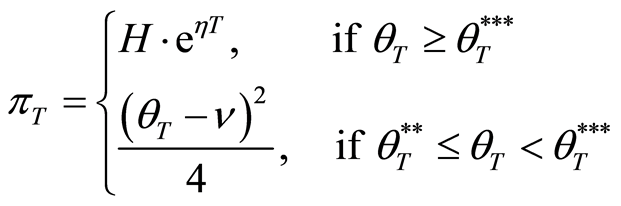
where 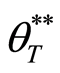
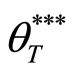
From above explanation, the benefit function for all situations at the maturity date T is as follows:
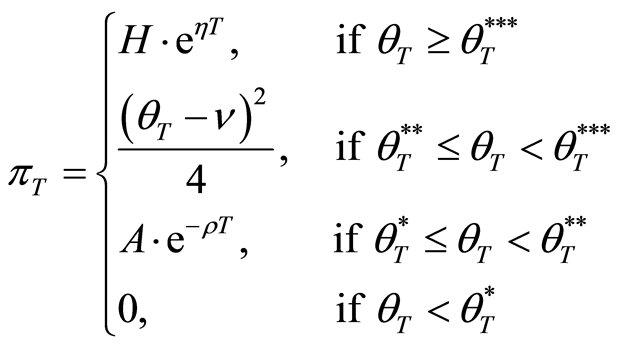
where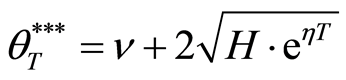
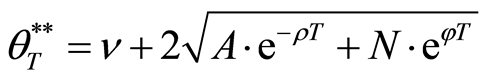
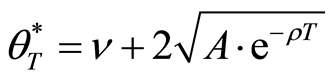
3.3. Two-Stage Decisions with Abandonment at Pre-Dependent Time t1 and Maturity T
According to assumptions in the Subsection 3.1, the valuation of the project is transformed as a contingent claim that depends on the underlying random valuable
The underlying 

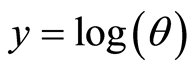
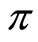
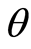
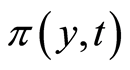
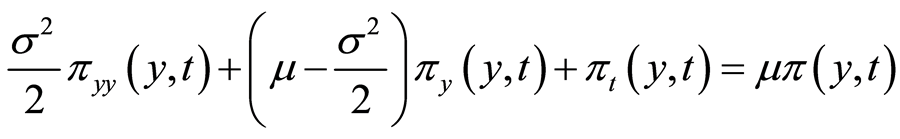
Then, the Equation (8) can be transformed to the Heat Equation (9) by the variable transformation (10).
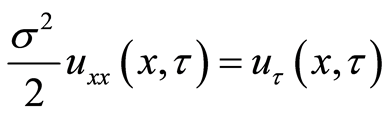
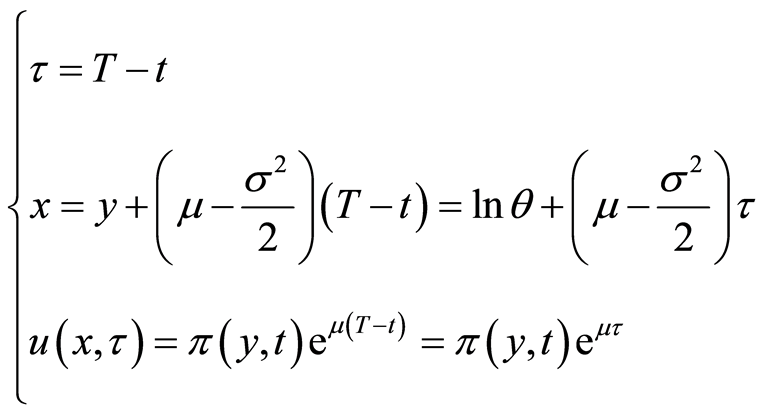
Therefore, the maturity date T will become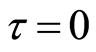
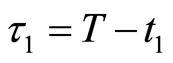


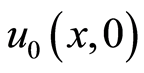
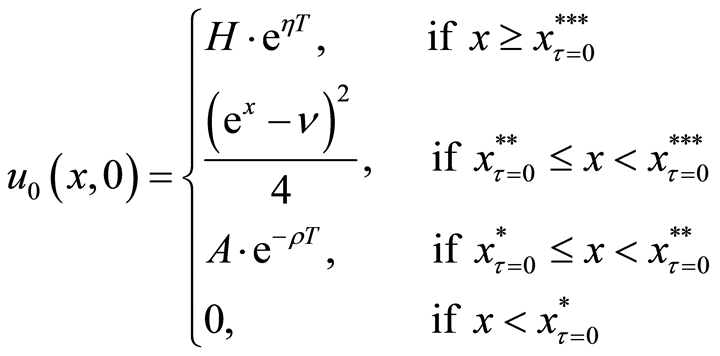
where
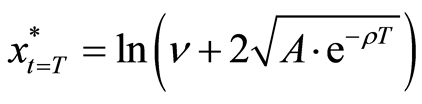
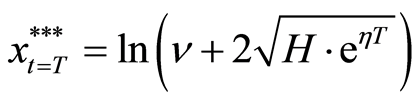
We adapt the most useful method—Green’s function to solve the heat Equation (9). The translated valuation 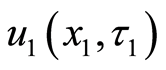
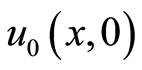
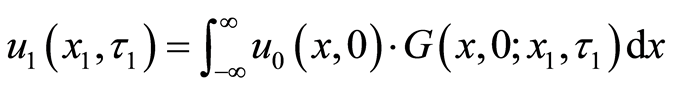
where Green’s function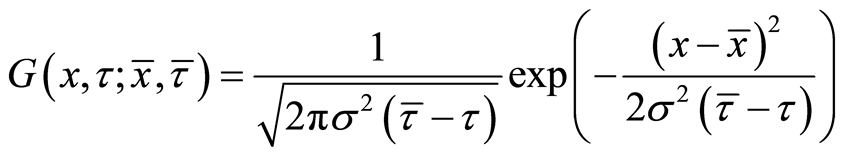
We combine the result 

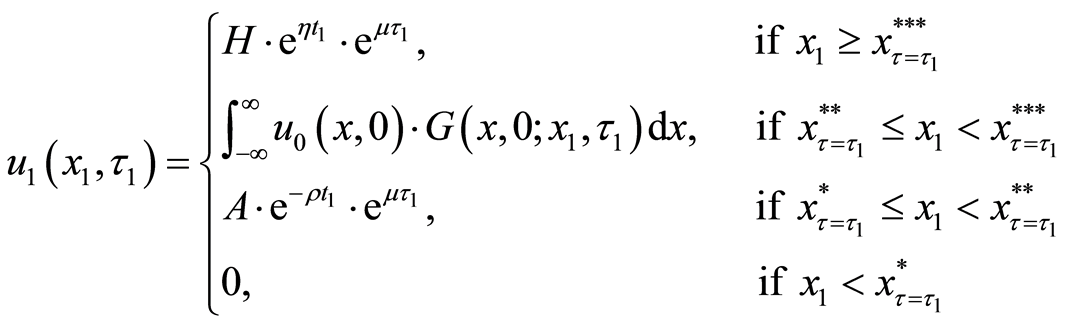
where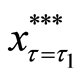
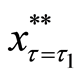
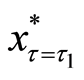
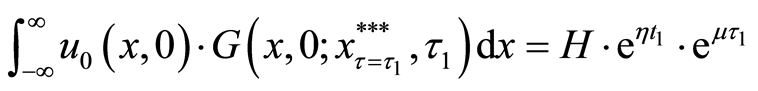
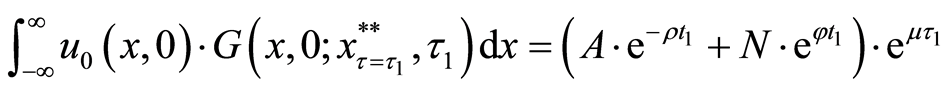
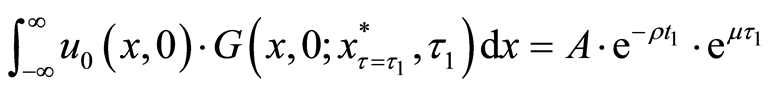
Therefore, we can graph Equation (13), the translated valuation of the project in each interval and each criterion of the threshold, as Figure 1.
After using the integral representation with Green’s function, the present translated valuation of the project can be presented as follows:
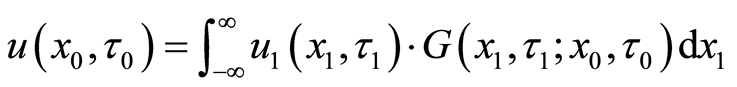
Finally, we can obtain the present valuation of the project as Equation (18).
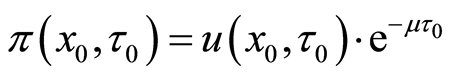
Figure 1. The translated valuation of real option with abandonment between each criterion of the threshold at predetermined policy-making point
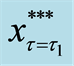
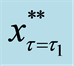
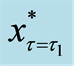
3.4. Two-Stage Decisions with Abandonment and Reset Investment Proportion at Pre-Dependent Time t1 and Maturity T
The demand is changing with time in the real world, so the investment of the project should adjust accordingly to cope with the situation in the market. For example, when the forecasted demand increases, we add the investment proportion of the project at the policy-making point. Then we set the increasing proportion for the demand of population to be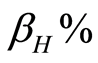
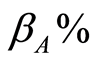

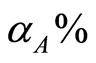
The policy-making depends on the situation of the transformed random variable x at time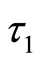
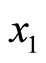

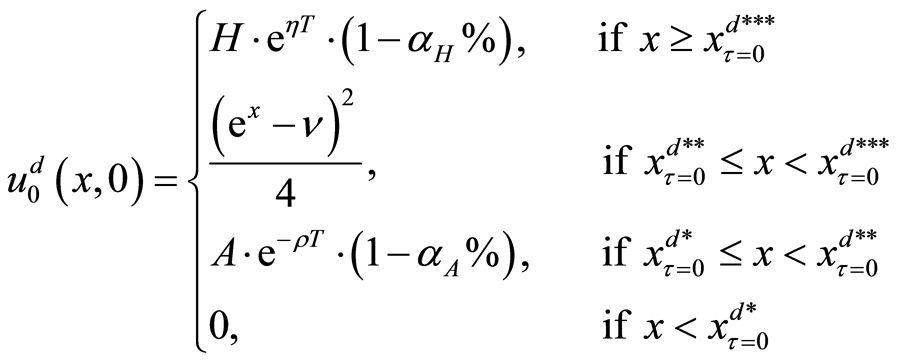
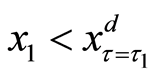
where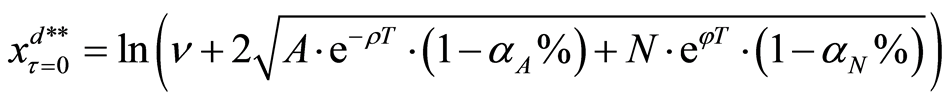
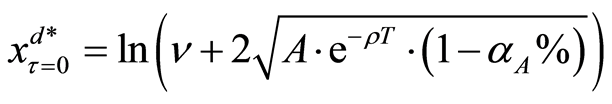

The translated valuation of the project after reducing investment at the policy-making point is as equation (20).
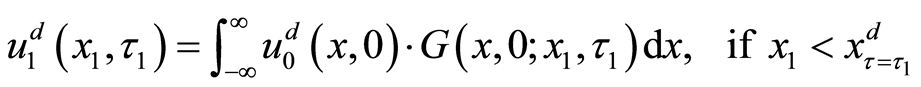
The criterion 
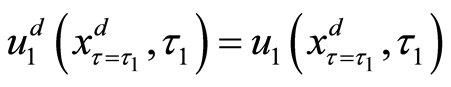
That is,
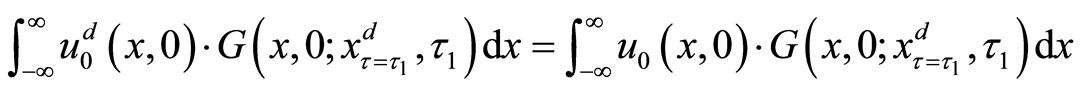
On the contrary, when 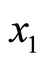
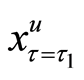

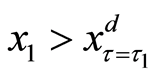
where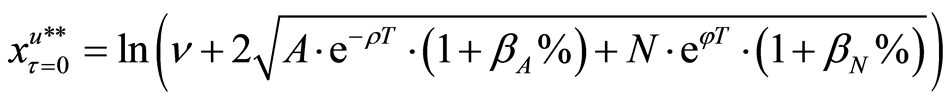


The translated valuation of the project after adding investment at the policy-making point is as Equation (23).
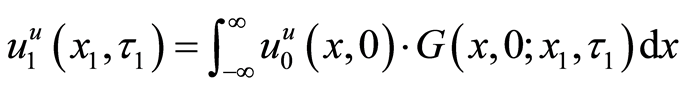
The criterion 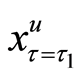
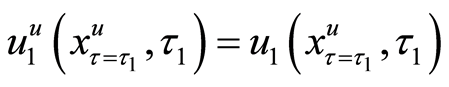
That is,
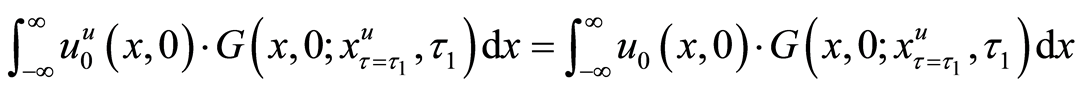
That is, when random variable 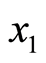

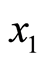
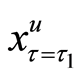
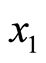
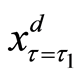
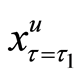
Furthermore, when the operating benefit of the project is too bad after reducing the investment of the project at the policy-making point, we will even consider to close the project and to sell the facilities to the market with its depreciation value. Hence, the criterion of the threshold 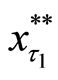

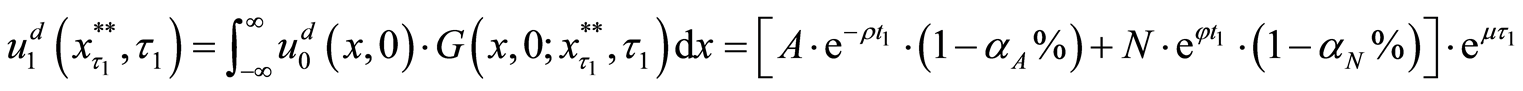
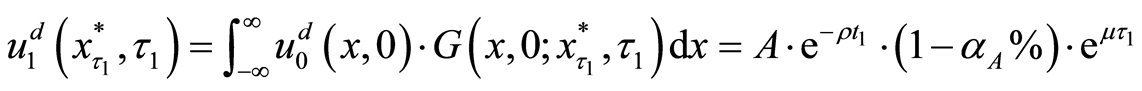
On the other hand, if the operating benefit of the project is very good after adding investment, even over the upper bound of production of the factory, the critical value 

Comparing with Equation (13), we can rearrange above equations as Equation (28). Figure 2 illustrates the translated valuation of the project in all situations between each critical value. For example, when the random variable is lesser than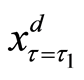
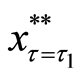
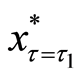
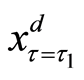

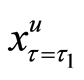
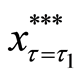
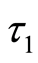
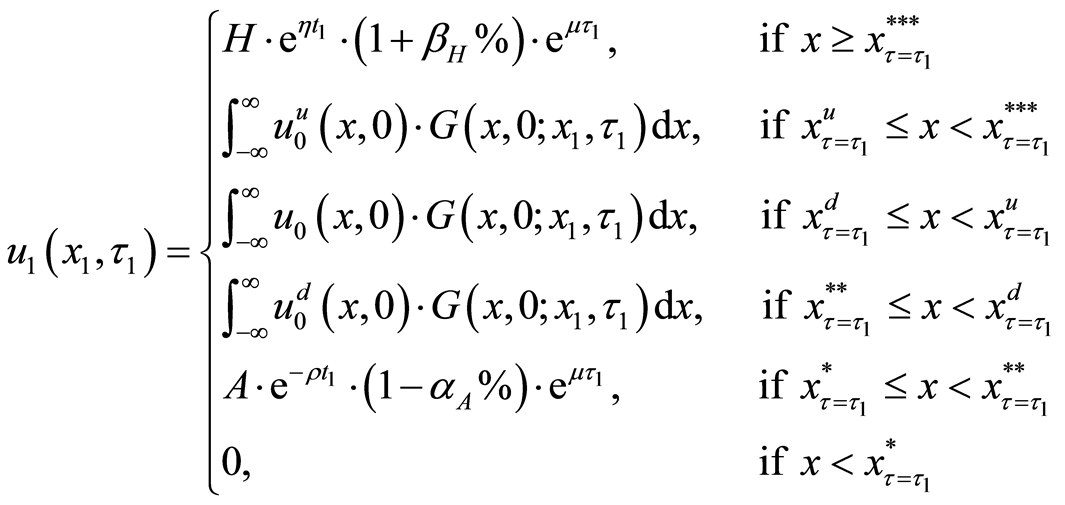
Figure 2. The translated valuation of real option with abandonment and reset investment proportion between each criterion of the threshold at predetermined policy-making point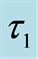
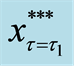

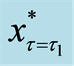
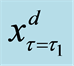
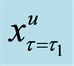
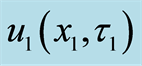
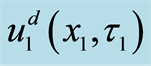
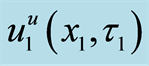
where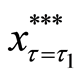
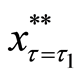
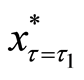
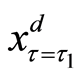
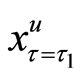
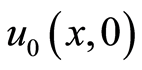
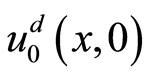
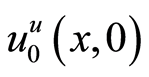
sent as Equations (12), (20), and (23), respectively.
Equation (28) will be the initial condition of PDE in the next interval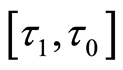

Then, the valuation of the project at present time to maturity 
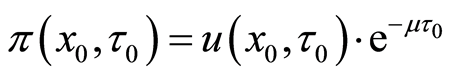
4. Conclusions
We discuss the valuation of the project in a firm applying real option with abandonment and reset investment proportion. We take the depreciation value of the facilities, the research and development (R & D) fee into consideration in this study. The traditional method to evaluate a project is by the net present value (NPV) or discount cash flow (DCF). Many scholars reported that above methods were hard to catch the uncertainty of the market in time. It would undervalue or miss the opportunity value of the investments, so the managers cannot make the optimal policy to the project immediately during a short time when the transient investment opportunity appears.
Our suggestion is to evaluate the project in a firm with the valuation of real options with abandonment and reset investment proportion. The advantage is that we can adjust the investment proportion according to the situation of the market, even abandon the project to reduce our loss. When we reduce the investment proportion to some level in the project, we would rather stop the project and sell the facilities to cover our loss. We could improve our method to derive a multi-stage decision model or a continuous decision model in the further researches.
References
- Robichek, A.A. and Horne, J.C.V. (1967) Abandonment Value and Capital Budgeting. Journal of Finance, 22, 577- 589.
- Dyl, E.A. and Long, H.W. (1969) Abandonment Value and Capital Budgeting: Comment. The Journal of Finance, 24, 88-95. http://dx.doi.org/10.1111/j.1540-6261.1969.tb00345.x
- Hayes, R. and Garvin, D. (1982) Managing as If Tomorrow Mattered. Harvard Business Review, 60, 71-79.
- Gray, S. and Whaley, R. (1999) Reset Put Options: Valuation, Risk Characteristics, and an Application. Australian Journal of Management, 24, 1-20. http://dx.doi.org/10.1177/031289629902400101
- Boyle, P.P. and Lau, S.H. (1994) Bumping up against the Barrier with the Binomial Method. Journal of Derivatives, 2, 6-14. http://dx.doi.org/10.3905/jod.1994.407891
- Cheng, W. and Zhang, S. (2000) The Analytics of Reset Options. Journal of Derivatives, 8, 59-71. http://dx.doi.org/10.3905/jod.2000.319114
- Boyle, P.P., Kolkiewicz, A.W. and Tan, K.S. (2001) Valuation of the Reset Options Embedded in Some Equity-Linked Insurance Product. North American Actuarial Journal, 5, 1-18. http://dx.doi.org/10.1080/10920277.2001.10595994
- Kimura, T. and Shinohara, T. (2004) Monte Carlo Analysis of Convertible Bonds with Reset Clauses. European Journal of Operational Research, 168, 301-310. http://dx.doi.org/10.1016/j.ejor.2004.07.008
- Ritchken, P. (1995) On Pricing Barrier Options. Journal of Derivatives, 3, 19-28. http://dx.doi.org/10.3905/jod.1995.407939
- Broadie, M., Glasserman, P. and Kuo, S. (1999) Connecting Discrete and Continuous Path-Dependent Options. Finance and Stochastics, 3, 55-82. http://dx.doi.org/10.1007/s007800050052
- Hörfelt, P. (2003) Extension of the Corrected Barrier Approximation by Broadie, Glassman, and Kou. Finance and Stochastics, 7, 231-243. http://dx.doi.org/10.1007/s007800200077
- Ahn, D., Figlewski, S. and Gao, B. (1999) Pricing Discrete Barrier Options with an Adaptive Mesh Model. Journal of Derivatives, 2, 33-44. http://dx.doi.org/10.3905/jod.1999.319127
- Kulatilaka, N. and Perotti, E.C. (1998) Strategic Growth Option. Management Science, 44, 1021-1031. http://dx.doi.org/10.1287/mnsc.44.8.1021