Open Journal of Clinical Diagnostics
Vol.4 No.2(2014), Article
ID:46100,7
pages
DOI:10.4236/ojcd.2014.42013
Bayesian Decision Analysis for Recurrent Cervical Cancer
Chi-Chang Chang1,2
1School of Medical Informatics, Chung Shan Medical University, Taichung, Chinese Taipei 2Information Technology Office of Chung Shan Medical University Hospital, Taichung, Chinese Taipei
Email: changintw@gmail.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 April 2014; revised 10 May 2014; accepted 18 May 2014
ABSTRACT
Risk modeling for recurrent cervical cancer requires the development of new concepts and methodologies. Unlike most daily decisions, many medical decision making have substantial consequences, and involve important uncertainties and trade-offs. The uncertainties may be about the accuracy of available diagnostic tests, the natural history of the cervical cancer, the effects of treatment in a patient or the effects of an intervention in a group or population as a whole. With such complex decisions, it can be difficult to comprehend all options “in our heads”. This study applied Bayesian decision analysis to an inferential problem of recurrent cervical cancer in survival analysis. A formulation is considered where individual was expected to experience repeated events, along with concomitant variables. In addition, the sampling distribution of the observations is modelled through a proportional intensity Nonhomogeneous Poisson process. The proposed decision models can provide decision support techniques not only for taking action in the light of all available relevant information, but also for minimizing expected loss. The decision process is useful in selecting the best alternative when a patient with recurrent cervical cancer, in particular, the proposed decision process can provide more realistic solutions.
Keywords
Bayesian Inference, Recurrent Event, Nonhomogeneous Poisson Process, Cervical Cancer

1. Introduction
Cervical cancer remains one of the leading causes of cancer-related death among women globally [1] [2] . Even though the morbidity and the mortality have been decreasing in recent years, the morbidity rates of cervical cancer are the second leading type in women and the mortality rates are the sixth of the top ten cancers in Taiwan. Because cervical cancer is a cancer which can be controlled and avoided, the studies related to the causes of and the treatment to the cervical cancer has been described sufficiently in lots of advanced researches. The cure rate of cervical carcinoma is quite high if detected early, but approximately 30% of International Federation of Gynecology and Obstetrics (FIGO) stage IB2 to stage IV disease will ultimately recur with modern multimodality treatment [3] [4] . There are few researches on its relationship between recurrent events and the mortality and incidence rate. Indeed, recurrent cervical cancer is a devastating disease for those women unfortunate enough to suffer such an event. Patients with recurrent disease or pelvic metastases have a poor prognosis with a 1-year survival rate between 15% and 20% [5] . Once the primary treatment has failed, the opportunity of secondary cure is slim. Probably several factors exist which indeed affect the ultimate prognosis of early stage cervical carcinoma other than clinical staging. Since, the treatment of recurrent cervical cancer is still a clinical challenge. When the recurrence is not surgically resectable, and/or suitable for curative radiation, therapeutic options are limited. In other words, early detection of recurrence may impact survival. Moreover, detection of asymptomatic recurrences is associated with prolonged overall survival and survival from the time of initial detection of recurrence [6] -[8] . Therefore, this paper attempts to improve surveillance after treatment might lead to earlier detection of relapse, and precise assessment of recurrent status could improve outcome.
2. Nonhomogeneous Possion Process (NHPP)
In order to model the recurrent cervical cancer, the Nonhomogeneous Poisson process (NHPP) was introduced to make the time-dependent behavior of more cervical cancer tractable [9] . The assumption that the survival after a medication is essentially the same as it was immediately before the recurrent event is plausible. Based on the assumption, the recurrent cervical cancer is time-dependent [9] . The intensity function of the failure process is usually assumed to be of the form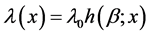 , where λ0 is the scale factor, β is the aging rate, x is the elapsed time, and h(.) can be any function that reflects the recurrent cervical cancer.
, where λ0 is the scale factor, β is the aging rate, x is the elapsed time, and h(.) can be any function that reflects the recurrent cervical cancer.
Suppose we have a patient with cervical cancer who recurrent process is given by a NHPP. We observe cervical cancer for x* units of time, during which we observe N recurrent events. In this (time-truncated) case, x* is a constant and N is a random variable. It is known for such an NHPP that the joint density function of the first N recurrent times is
 (1)
(1)
where 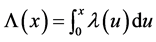 is the mean number of recurrent events by time x in the nonhomogeneous Poisson process. If we instead observe the cervical cancer until the n*th recurrent event (rather than until time x*), and the n*th recurrent time occurs at time Xn* (i.e., the recurrent event-truncated case, where n* is a constant and Xn* is a random variable), then the joint density function of the first n* recurrent times is
is the mean number of recurrent events by time x in the nonhomogeneous Poisson process. If we instead observe the cervical cancer until the n*th recurrent event (rather than until time x*), and the n*th recurrent time occurs at time Xn* (i.e., the recurrent event-truncated case, where n* is a constant and Xn* is a random variable), then the joint density function of the first n* recurrent times is
 (2)
(2)
The recurrent cervical cancer is modeled by a power law failure model if it is given by an NHPP with an intensity function of the form

![]() (3)
(3)
where β is effectively unit. When β is equal to one, the NHPP degenerates to an HPP with a constant β0. For β < 1 the failure intensity is decreasing (corresponding to survival growth), and for β > 1 the failure intensity is increasing. Note that for 1 < β the failure intensity is concave downward, and for β > 2 the failure intensity is concave upward.
Other failure models have also been proposed to model recurrent process, but in more complicated ways. Unlike the power law failure model given above, these models often have more than two parameters. This makes the analysis more difficult. But since some of these models are generated by combining two of the three commonly used models. For example, the exponential polynomial rate model proposed by Cox [10] is of the form
 the Weibull and log-linear rate model proposed by Lee [11] is of the form
the Weibull and log-linear rate model proposed by Lee [11] is of the form
![]() the nonlinear failure rate model proposed by Salem [12] is of the form
the nonlinear failure rate model proposed by Salem [12] is of the form
 the bounded intensity model proposed by Hartler [13] is of the form
the bounded intensity model proposed by Hartler [13] is of the form
 the gamma type intensity model proposed by Yamada et al. [14] is of the form
the gamma type intensity model proposed by Yamada et al. [14] is of the form
![]() and the bathtub type failure rate models
and the bathtub type failure rate models  and
and ![]() are proposed by Calvin [15] and Hjorth [16] , respectively.
are proposed by Calvin [15] and Hjorth [16] , respectively.
In this paper, we develop a Bayesian decision process for the power law failure model, since the power law intensity function allows for a wide variety of shapes (including both concave upward and concave downward, as well as decreasing) and tends not to increase very steeply, which may make it more realistic for clinical practices.
3. Bayesian Inference
Suppose a patient with recurrent cervical cancer that behaves according to the nonhomogeneous Poisson process with intensity function . The crucial two-action decision is whether after some period of time t, the failure rate of the recurrent cervical cancer will be too high (in which case some undertaking the intervention treatment needs to be taken), or will still be within an acceptable range (in which case we can according to the status quo). Another option is to gather additional information. The decision should be made on the basis of expected cost-effectiveness with respect to some loss function [17] [18] . We also assume that the decision maker is risk neutral, and can therefore make the decision on the basis of expected monetary value. The basic elements of the Bayesian decision process are as follows:
. The crucial two-action decision is whether after some period of time t, the failure rate of the recurrent cervical cancer will be too high (in which case some undertaking the intervention treatment needs to be taken), or will still be within an acceptable range (in which case we can according to the status quo). Another option is to gather additional information. The decision should be made on the basis of expected cost-effectiveness with respect to some loss function [17] [18] . We also assume that the decision maker is risk neutral, and can therefore make the decision on the basis of expected monetary value. The basic elements of the Bayesian decision process are as follows:
Parameter space Θ: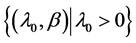 , where λ0 is the scale factor and β is the aging rate. Both parameters are uncertain and can be estimated through physicians’ opinions.
, where λ0 is the scale factor and β is the aging rate. Both parameters are uncertain and can be estimated through physicians’ opinions.
Action space A:{a1,a2}, where a1 is the status quo, and a2 is the risk reduction action. (We eventually expand this to consider a third possible action, the collection of additional information).
Loss function L: a real function defined on Θ × A. If we decide to keep continuing the status quo, then the loss we face is L(θ,a1); if we decide to take the risk reduction action, then the loss we face is L(θ,a2).
Sample space S: The additional information available to be collected. With recurrent event-time endpoints, it is common to schedule analyses at the times of occurrence of specified landmark events, such as the 5th event, the 10th event, and so on. The collecting this additional data or information should also be reflected in the decision process.
The cost of collecting this additional information should also be reflected in the decision process. The detailed analysis descriptions of each phase are as follows:
3.1. Prior Analysis
The available prior clinical knowledge (e.g., physician’s opinion, past experience, or the similar clinical status) about the parameter space,  , can be represented by a joint distribution indicating the relative likelihood of each state of nature. Loss functions appropriate for the status quo a1 and risk reduction action a2 can be derived by taking all cost-related data into account. Once the prior distribution and loss function have been specified, it is easy to perform a prior analysis by simply comparing the expected losses for the options a1 and a2. Therefore, if
, can be represented by a joint distribution indicating the relative likelihood of each state of nature. Loss functions appropriate for the status quo a1 and risk reduction action a2 can be derived by taking all cost-related data into account. Once the prior distribution and loss function have been specified, it is easy to perform a prior analysis by simply comparing the expected losses for the options a1 and a2. Therefore, if , then option a2 is optimal, and if
, then option a2 is optimal, and if , then option a1 is optimal.
, then option a1 is optimal.
3.2. Preposterior Analysis
When the expected losses associated with options a1 and a2 are fairly close, we might not feel very confident about a decision based solely on a prior analysis, and gathering additional information might be desirable. However, before collecting additional information, we have to investigate the possible outcomes and costs of each candidate sampling plan, and to determine the first stage decision of whether collecting additional information is worthwhile and also which sampling plan is the best in terms of cost-effectiveness. The Expected Value of Sample Information (EVSI) can be calculated according to
 where
where 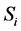 is the ith sampling plan under consideration. The Expected Net Gain of Sample information (ENGS)
is the ith sampling plan under consideration. The Expected Net Gain of Sample information (ENGS)
is defined as , where
, where  is the cost of the ith sampling plan. Therefore, if ENGS ≤ 0, then it is not worthwhile collecting additional information; conversely, if ENGS > 0, then we can start collecting data and prepare for a posterior analysis, and the i*th sampling plan should be adopted in order to satisfy the condition
is the cost of the ith sampling plan. Therefore, if ENGS ≤ 0, then it is not worthwhile collecting additional information; conversely, if ENGS > 0, then we can start collecting data and prepare for a posterior analysis, and the i*th sampling plan should be adopted in order to satisfy the condition .
.
3.3. Posterior Analysis
Once the optimal sampling plan, say S(k), has been selected based on the preposterior analysis. After the data collection is complete, the observed data S(k) = s(k) can then be used to perform a posterior analysis. The decision should then be made in accordance with the strategy that if
 then option a2 is optimal, and if
then option a2 is optimal, and if
 then option a1 is optimal.
then option a1 is optimal.
By exploring the relationships among the optimal decision and the extent of uncertainty about recurrent trends, the conditions under which gathering additional information is worthwhile can be determined, and more generally in developing guidelines for the use of isolating trends in data in risk management. The following terminology will be used throughout this paper:
CA: the cost of a recurrent event if it occurs.
CR: the cost of the proposed risk reduction action.
CI: the cost of collecting additional information.
ρ: the reduction in failure rate that would result from the proposed risk reduction action (0 < ρ < 1).
M: the expected number of failures during the time period [t,T] under the status quo.
Suppose that patient has a planned lifetime T, and the decision of whether to keep the status quo or perform some intervention treatment must be made at time t. The decision variable we are dealing with is then the expected number of recurrent event during the time period [t,T]. Since recurrent times are assumed to be drawn from a nonhomogeneous Poisson process with intensity function , the expected number of recurrent events in [t,T] under the status quo is given by
, the expected number of recurrent events in [t,T] under the status quo is given by
 (4)
(4)
where![]() , and H ≡ H
, and H ≡ H . Suppose that undertaking the intervention treatment will reduce the failure intensity by a fraction ρ, where
. Suppose that undertaking the intervention treatment will reduce the failure intensity by a fraction ρ, where . Then the expected number of recurrent events in [t,T] if undertaking the intervention treatment is performed is given by
. Then the expected number of recurrent events in [t,T] if undertaking the intervention treatment is performed is given by
![]() (5)
(5)
On the basis of the assumptions given above, we therefore have a two-action problem with a linear loss function, where the loss for taking action a1 (i.e., continuing with the status quo) is CAM and the loss for taking action a2 (i.e., undertaking the intervention treatment) is . The expected loss for the status quo is simply
. The expected loss for the status quo is simply , and the expected loss for undertaking the intervention treatment is
, and the expected loss for undertaking the intervention treatment is , and
, and  is the cutoff value of E{M} for undertaking the intervention treatment.
is the cutoff value of E{M} for undertaking the intervention treatment.
As a simplistic assumption, one can assume that λ0 and β are independent of each other. For example, if the prior distributions for λ0 and β are Gamma ( ;
;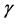 ) and Uniform (a,b), respectively, and the power-law failure model is assumed to be suitable under consideration, then the joint distribution of λ0 and β is just the product of the individual distributions of λ0 and β. The joint posterior distribution for λ0 and β obtained by Bayesian updating is simply proportional to the product of the joint prior distribution for λ0 and β and the likelihood function, which is given by
) and Uniform (a,b), respectively, and the power-law failure model is assumed to be suitable under consideration, then the joint distribution of λ0 and β is just the product of the individual distributions of λ0 and β. The joint posterior distribution for λ0 and β obtained by Bayesian updating is simply proportional to the product of the joint prior distribution for λ0 and β and the likelihood function, which is given by
 (6)
(6)
where K is the normalizing constant.
Since the prior and posterior density functions for M are functions of λ0 and β, some prior and posterior mean values of M can be derived by the bivariate transformation technique. However, closed forms for the prior and posterior means of M are not always available, which is typically the case for the Bayesian analysis. Nevertheless, Bayesian prior and posterior analyses can still be performed by computing the prior and posterior mean values of M using the numerical integration technique and comparing them with the cutoff value 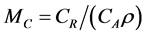 (i.e., the cutoff value of E{M} for taking the risk reduction action). If the relevant mean is smaller than MC, then we should keep the status quo; if not, then we should perform the risk reduction action.
(i.e., the cutoff value of E{M} for taking the risk reduction action). If the relevant mean is smaller than MC, then we should keep the status quo; if not, then we should perform the risk reduction action.
4. Simulation Study
We have used the recurrent cervical cancer case study to illustrate the use of the models developed in the previous sections. The medical records and pathology were accessible by the Chung Shan Medical University Hospital Tumor Registry. The birth date of the studied subject was 1-May-1943, and the observation period was from 24-Sep-2010, to 23-August-2011. The recurrent dates for the subject during the observation period were: {24-Jan-2011, 24-Apr-2011, 24-May-2011, 23-Jul-2011, 22-Aug-2011}. An application is performed with the assumption that E{λ0} = 0.2 and SD{λ0} = 0.03, and that β is Uniform[1,2.8]. In addition, we have CA = 238,000, CR = 196,000, CI = 102,000, ρ = 0.08, T = 75, and t = 62. We use the entire failure data for the posterior analysis. Prior and posterior analyses are performed by comparing the prior and posterior mean values of M with the cutoff value MC.
Since the recurrent data are already available, we assume that the cost of analyzing the recurrent data is associated with tasks such as reviewing records and interviewing physicians. As can be seen in the Table 1, prior
and posterior analyses can be performed by comparing the prior and posterior mean values of λ0 with the cutoff value MC. The observed data support the adoption of the risk reduction action, whereas the priors support the status quo. This can be explained by the fact that the observed data indicate greater deterioration than was assumed by the prior distributions.
5. Conclusion
In this study, Bayesian inference of a nonhomogeneous Poisson process with power law failure intensity function was used to describe the behavior of recurrent cervical cancer. In particular, the proposed priors allow us to explicitly account for independence between λ0 and β, and are a significant improvement over previous approaches, which have generally been based on the assumption either that β is known or that λ0 and β are independent. Furthermore, the prior distribution for the power law failure model has more advantages than the corresponding distribution for any other failure models, since it has a wide range of intensity function shapes. The proposed decision models can provide decision support techniques not only for taking action in the light of all available relevant information, but also for minimizing expected loss. One area in which further work might be desirable is to study other failure models (e.g., the proportional hazard model, the exponential polynomial rate model, the Weibull and log linear rate model, the nonlinear failure rate model, or the bathtub type failure rate model) using the same procedure developed in this study. However, since these models usually have more than two parameters, the analysis will be more complicated.
References
- Goldie, S.J., Kuhn, L., Denny, L., Pollack, A. and Wright, T. (2001) Policy Analysis of Cervical Cancer Screening Strategies in Low-Resource Setting: Clinical Benefits and Cost Effectiveness. The Journal of the American Medical Association, 285, 3107-3115. http://dx.doi.org/10.1001/jama.285.24.3107
- Parkin, D.M., Bray, F.I. and Devesa, S.S. (2001) Cancer Burden in the Year 2000: The Global Picture. European Journal of Cancer, 37, S4-S66. http://dx.doi.org/10.1016/S0959-8049(01)00267-2
- Lai, C.H., Hong, J.H., Hsueh, S, et al. (1999) Preoperative Prognostic Variables and the Impact of Postoperative Adjuvant Therapy on the Outcomes of Stage IB or II Cervical Carcinoma Patients with or without Pelvic Lymph Node Metastases. Cancer, 85, 1537-1546. http://dx.doi.org/10.1002/(SICI)1097-0142(19990401)85:7<1537::AID-CNCR15>3.0.CO;2-6
- Waggoner, S.E. (2003) Cervical Cancer. Lancet, 361, 2217-2225.http://dx.doi.org/10.1016/S0140-6736(03)13778-6
- Berek, J.S. and Hacker, N.F. (2005) Practical Gynaecologic Oncology. Lippincott Williams & Wilkins, New York.
- Berger, J.O. and Bernardo, J.M. (1992) Ordered Group Reference Priors with Applications to a Multinomial Problem. Biometrika, 79, 25-37. http://dx.doi.org/10.1093/biomet/79.1.25
- Chang, C.C. and Cheng, C.S. (2007) A Structural Design of Clinical Decision Support System for Chronic Diseases Risk Management. Central European Journal of Medicine, 2, 129-139.
- Chang, C.C. (2008) Bayesian Value of Information Analysis with Linear, Exponential, Power Law Failure Models for Aging Chronic Diseases. Journal of Computing Science and Engineering, 2, 201-220.
- Chang, C.C., Cheng, C.S. and Huang, Y.S. (2006) A Web-Based Decision Support Systems for Chronic Disease. Journal of Universal Computer Science, 12, 115-125.
- Cox, D.R. and Lewis, P.A.W. (1966) The Statistical Analysis of Series of Events. Chapman and Hall Press, London. http://dx.doi.org/10.1007/978-94-011-7801-3
- Lee, L. (1980) Testing Adequacy of the Weibull and Log Linear Rate Models for a Poisson Process. Technometrics, 22, 195-199. http://dx.doi.org/10.1080/00401706.1980.10486134
- Salem, S.A. (1992) Bayesian Estimation of a Non-Linear Failure Rate from Censored Samples Type II. Microelectronics and Reliability, 32, 1385-1388. http://dx.doi.org/10.1016/0026-2714(92)90007-8
- Hartler, G. (1989) The Nonhomogeneous Poisson Process—A Model for the Reliability of Complex Repairable Systems. Microelectronics and Reliability, 29, 381-386. http://dx.doi.org/10.1016/0026-2714(89)90624-0
- Yamada, S., Hishitani, J. and Osaka, S. (1992) Software Reliability Measurement and Assessment Based on Nonhomogeneous Poisson Process Models: A Survey. Microelectronics and Reliability, 32, 1763-1773. http://dx.doi.org/10.1016/0026-2714(92)90272-M
- Calvin, T.W. (1973) Modeling the Bathtub Curve in ARMS. IEEE 73CHO714-GR, 577-582.
- Hjorth, U. (1980) A Reliability Distribution with Increasing, Decreasing, Constant and Bathtub-Shaped Failure Rates. Technometrics, 22, 99-107. http://dx.doi.org/10.2307/1268388
- Parmigiani, G., Samsa, G.P., Ancukiewicz, M., Lipscomb, J., Hasselblad, V. and Matchar, D.B. (1997) Assessing Uncertairity in Cost-Effectiveness Analyses: Application to a Complex Decision Model. Medical Decision Making, 17, 390-401. http://dx.doi.org/10.1177/0272989X9701700404
- Hunink, M.G.M., Bult, J.R., Vries, J.D. and Weinstein, M.C. (1998) Uncertainty in Decision Models Analyzing Cost Effectiveness; The Join Distribution of Incremental Costs and Effectiveness Evaluated with a Nonparametric Bootstrap Method. Medical Decision Making, 18, 337-346. http://dx.doi.org/10.1177/0272989X9801800312


