Open Journal of Discrete Mathematics
Vol.05 No.03(2015), Article ID:58086,4 pages
10.4236/ojdm.2015.53003
Independence Numbers in Trees
Min-Jen Jou1, Jenq-Jong Lin2
1Department of Information Technology, Ling Tung University, Taichung Taiwan
2Department of Finance, Ling Tung University, Taichung Taiwan
Email: mjjou@teamail.tu.edu.tw, jjlin@teamail.tu.edu.tw
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 March 2015; accepted 14 July 2015; published 17 July 2015
ABSTRACT
The independence number 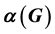 of a graph G is the maximum cardinality among all independent sets of G. For any tree T of order n ≥ 2, it is easy to see that
of a graph G is the maximum cardinality among all independent sets of G. For any tree T of order n ≥ 2, it is easy to see that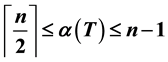 . In addition, if there are duplicated leaves in a tree, then these duplicated leaves are all lying in every maximum independent set. In this paper, we will show that if T is a tree of order n ≥ 4 without duplicated leaves, then
. In addition, if there are duplicated leaves in a tree, then these duplicated leaves are all lying in every maximum independent set. In this paper, we will show that if T is a tree of order n ≥ 4 without duplicated leaves, then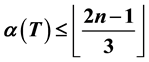 . Moreover, we constructively characterize the extremal trees T of order n ≥ 4, which are without duplicated leaves, achieving these upper bounds.
. Moreover, we constructively characterize the extremal trees T of order n ≥ 4, which are without duplicated leaves, achieving these upper bounds.
Keywords:
Independent Set, Independence Number, Tree

1. Introduction
All graphs considered in this paper are finite, loopless, and without multiple edges. For a graph G, we refer to 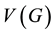 and
and 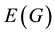 as the vertex set and the edge set, respectively. The cardinality of
as the vertex set and the edge set, respectively. The cardinality of 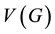 is called the order of G, denoted by
is called the order of G, denoted by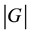 . The (open) neighborhood
. The (open) neighborhood 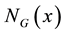 of a vertex x is the set of vertices adjacent to x in G, and the close neighborhood
of a vertex x is the set of vertices adjacent to x in G, and the close neighborhood 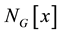 is
is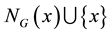 . A vertex x is said to be a leaf if
. A vertex x is said to be a leaf if . A vertex v of G is a support vertex if it is adjacent to a leaf in G. Two distinct vertices u and v are called duplicated if
. A vertex v of G is a support vertex if it is adjacent to a leaf in G. Two distinct vertices u and v are called duplicated if . Note that u and v are duplicated vertices in a tree, and then they are both leaves. The n-path
. Note that u and v are duplicated vertices in a tree, and then they are both leaves. The n-path 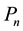 is the path of order
is the path of order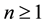 . For a subset
. For a subset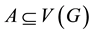 , the induced subgraph induced by A is the graph
, the induced subgraph induced by A is the graph 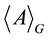 with vertex set A and the edge set
with vertex set A and the edge set


A set 





The independence problem is to find an 
any tree T of order



characterize the extremal trees T of order
2. The Upper Bound
In this section, we will show a sharp upper bound on the independence number of a tree T without duplicated leaves.
Lemma 1 If H is an induced subgraph of G, then
Proof. If S is an 

Lemma 2 ([4] ) If T is a tree of order

Lemma 3 ([5] ) If T is a tree of order

Lemma 4 For an integer

Proof. It is straightforward to check that 









Theorem 1 If T is a tree of order 

Proof. We prove it by induction on
























Note that the result in Theorem 1 is sharp and some such T are illustrated below.
3. Extremal Trees
Let 


We will constructively characterize these extremal trees. Let 



Operation O1. Join a vertex 





Operation O2. Join a vertex 





Operation O3. Join a vertex u of 





Operation O4. Join a vertex 


Lemma 5 Suppose that 


Proof. It’s true for all



Hence we obtain that






This completes the proof.
Lemma 6 Let 






Proof. Suppose that 






set of 







Lemma 7 Let 









Proof. Note that such a tree T exists, as, for instance, the tree in Figure 1 is as desired. If 












Lemma 8 Let 





Proof. Note that T' is a tree of order n + 2 without duplicated leaves. And IO3 is an independent set of T' with







Lemma 9 Let 





Proof. Note that T' is a tree of order 






Let 




Theorem 2 T is in 

Figure 1. The trees T with
Proof. If T is in









Case 1. T' has no duplicated leaves.
For an 


Theorem 1, we have that







Case 2. T' has duplicated leaves z and z'.
Let









lows that




By Cases 1 and 2, we conclude that T is in

Now, we obtain the main theorem in this paper.
Theorem 3 Suppose that T is a tree of order 


Cite this paper
Min-JenJou,Jenq-JongLin, (2015) Independence Numbers in Trees. Open Journal of Discrete Mathematics,05,27-31. doi: 10.4236/ojdm.2015.53003
References
- 1. Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Application. North-Holland, New York.
- 2. Harant, J. (1998) A Lower Bound on the Independence Number of a Graph. Discrete Mathematics, 188, 239-243.
http://dx.doi.org/10.1016/S0012-365X(98)00048-X - 3. Hattingh, J.H., Jonack, E., Joubert, E.J. and Plummer, A.R. (2007) Total Restrained Domination in Trees. Discrete Mathematics, 307, 1643-1650.
http://dx.doi.org/10.1016/j.disc.2006.09.014 - 4. Jou, M.-J. (2010) Dominating Sets and Independent Sets in a Tree. Ars Combinatoria, 96, 499-504.
- 5. Jou, M.-J. (2010) Upper Domination Number and Domination Number in a Tree. Ars Combinatoria, 94, 245-250.
- 6. Luo, R. and Zhao, Y. (2006) A Note on Vizing’s Independence Number Conjecture of Edge Chromatic Critical Graphs, Discrete Mathematics, 306, 1788-1790.
http://dx.doi.org/10.1016/j.disc.2006.03.040













