Received 26 April 2016; accepted 24 May 2016; published 27 May 2016

ABSTRACT

Three Clifford algebras are sufficient to describe all interactions of modern physics: The Clifford algebra of the usual space is enough to describe all aspects of electromagnetism, including the quantum wave of the electron. The Clifford algebra of space-time is enough for electro-weak interactions. To get the gauge group of the standard model, with electro-weak and strong interactions, a third algebra is sufficient, with only two more dimensions of space. The Clifford algebra of space allows us to include also gravitation. We discuss the advantages of our approach.

Keywords:

Geometry, Invariance Group, Dirac Equation, Electromagnetism, Weak Interactions, Strong Interactions, Clifford Algebras, Gravitation

1. Introduction

Why Clifford algebras are necessary in physics? Physics uses waves and the Fourier theorem says that any periodic function may be decomposed in a sum of sin and cos functions. These functions are more easily studied with the complex exponential function. Moreover the exponential function is the main tool in Lie groups. The exponential function needs products, so we must also know how to multiply numbers and vectors and products of vectors: we need a Clifford algebra. Why space algebra? The first reason is simply that our physical space is 3-dimensional [1] . The second reason is the spin 1/2 of all fundamental fermions, which uses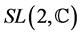, that is a subgroup of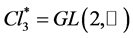. This greater group is the group of form invariance of electromagnetism, wave of the electron included [2] - [6] . And this form invariance rules [7] - [9] also the other kinds of interactions. We first recall how the group of the invertible elements in the space algebra 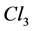acts. Time and space take naturally place in the auto-adjoint part of this algebra, with

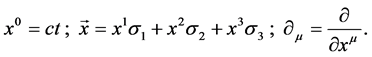(1)

Quantum mechanics lets, since 1927 [10] :

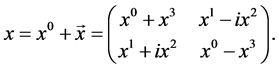(2)

Space-time is then the auto-adjoint part of the space algebra [1] :

(3)

This allows us to read the Dirac wave of the electron in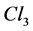. The link¹ with the old complex formalism is simple only if we use the left and right Weyl spinors and by letting:

(4)

being the transposed conjugate of M and also the reverse of M, we use and where is the scalar part, the vector part, the bivector or pseudo- vector part and the trivector or pseudo-scalar part of M. The conjugation is the main automorphism of:

(5)

With, , , our homogeneous non-linear wave equation for the electron, which has the Dirac equation as linear approximation, has the invariant form:

(6)

where,. It is invariant under any transformation R defined by an element M of the Lie group:²

(7)

Only one M term is present in the transformation of when two M terms are present in the transformation of x: consequently the wave turns with a angle when the space turns with a angle. The application

(8)

is not an isomorphism, but only an homomorphism from into a group of geometric transformations that we named Lorentz dilations. They are the product, in any order, of an element of the restricted³ Lorentz group by a homothety with ratio. The kernel of f is the chiral group generated by which orients the space. Consequently the chirality is essential in the standard model of quantum physics, it is present in the transformation of the wave (7). The chirality disappears in the geometry of space-time because it does not act in. Next, space-time vectors are contravariant if they satisfy and covariant

if they satisfy. Since and are similarly transformed, this allows the gauge invariance un-

der the electric gauge transformation which reads in:

(9)

We have three reasons for enlarging the group of invariance from into. First this enlargement is possible, which is surprising, because formulas (7) are satisfied with any M. Next the condition which is used to get only has no meaning in geometry, while the 3 of is simply the dimension of space. Finally the main reason is all that we understand from this enlargement. For instance the invariance of the product instead of the invariance of m and separately is the reason of the existence of the Planck constant [7] - [9] . The greater group of invariance has also induced the invariant form of the wave equation, and this will bring a new understanding of the existence of the Lagrangian density, and so on.

The space algebra is 8-dimensional on, therefore the invariant wave Equation (6) is equivalent to a system of 8 numeric equations with partial derivatives. In the basis of the numeric equations corresponding respectively to 1 and are [20]

(10)

where J is the current of density of probability and is the Lagrangian density. Then the law of conservation of the J current is a part of the wave equation and similarly is a part of the wave equation⁴. The wave equation comes from a Lagrangian mechanism and (this is new) the invariant wave equation contains. This explains why there is a principle of extremum in quantum mechanics⁵.

We have previously explained how classical electromagnetism, without or with magnetic monopoles, reads in space algebra (chapter 4 of [8] and [9] ):

(11)

where F is the electromagnetic field, A is the vector electric potential, is the pseudo-vector magnetic potential, j is the vector electric current and is the pseudo-vector magnetic current. Under the dilation R defined in (7), the A and B are contravariant vectors, moving with the source, while the j and k currents are covariant vectors and the field F satisfies:

(12)

2. Numeric Dimension

We name “numeric-dimension” of any physical quantity the power of the ratio in the formula giving the transformation of this quantity under the dilation R defined by any element M in. With this P is an element of, then (7) implies that x has numeric-dimension 1, implies that has numeric-dimension 1/2 and implies that and have numeric-dimension. (12) implies that the electromagnetic field (and this will be the same for all other gauge fields) has numeric-dimension 0. This is also the case for any velocity and for the fine structure constant. Using the contravariance of A and the covariance of we have established (see [12] Sec. 4.1.2) that an electric charge (and it is the same for a magnetic charge) has numeric-dimension 2 while a proper mass has numeric-dimension 3. is not constant under the full group of invariance and has numeric-dimension 4. Then a proper mass does not vary like an electric charge under a Lorentz dilation with ratio. An electric charge varies like a surface; a proper mass varies like a volume. There is a geometrical difference between a mass and a charge. The Planck factor has the numeric-dimension of a space-time volume. We must then consider that h is not a constant, it is a variable ratio between energy and frequency of a particle, variable only if.

This is important when we want to put together electromagnetism and gravitation. The numeric-dimension has also predictive value: we said previously, as anyone, that J is the current of probability, but the true current of probability is, as we shall see in Section 5.

3. The Electro-Weak Gauge in Space-Time Algebra

Two non equivalent homomorphisms [10] exist from into the group of dilations on the space-time:

(13)

This is the origin of the existence of left and right waves, that are fundamental for weak interactions. We have obtained [20] in the algebra a wave equation with mass term for the pair electron + neutrino, both form invariant (then relativistic invariant), and gauge invariant under the gauge group of electro-weak interactions. The wave of the electron + neutrino is a function of space and time with value in the space-time algebra. The form of this wave is determined by the invariance under. It reads:

(14)

where indices e, n, p and a indicate the respective waves of the electron, the electronic neutrino, the positron and the electronic anti-neutrino. They satisfy:

(15)

The Weinberg-Salam model [21] has no use for the right wave of the neutrino and cancels this term⁶. This gives

(16)

The charge conjugation is the same as in the standard model of quantum physics. Instead of the tensorial densities built from the wave of the electron⁷ we get now tensorial densities built from the parameters of the wave of electron + neutrino. 6 of them allows us to let:

(17)

The invariant wave equation of electron + neutrino reads

(18)

where is the reverse of and where reads:

(19)

with, right part of, , left part of. The covariant derivative uses four operators which form a basis of the Lie algebra of and reads:

(20)

The covariant derivative of electro-weak interactions uses:

(21)

with, , , for a doublet of left-handed particles and for a sing-

let of right-handed particle. Y is the weak hypercharge, , for the electron. Transposing into space-time algebra, we let

(22)

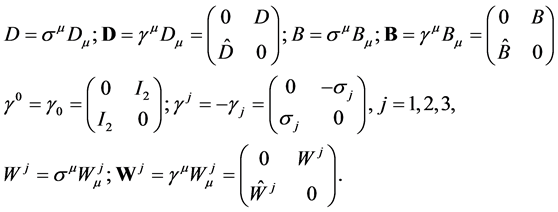
We have proved [7] - [9] [25] that the covariant derivative (21) of the Weinberg-Salam model is exactly equivalent to

(23)

The wave Equation (18) is invariant under the R transformation generated by any M element of, this invariance uses the isomorphism of into the even subalgebra such as:

(24)

This implies the relativistic invariance of the wave equation. It is also gauge invariant (exactly!) under the gauge transformation:

(25)

where is replaced by:

(26)

The proper mass in (18) is the proper mass of the lone electron, then with (19) the wave equation of electron + neutrino is reduced to the invariant wave Equation (6) when the wave of the electronic neutrino is canceled. If the wave of the electron is canceled the mass term is canceled and we get for the neutrino the Dirac equation without mass:

(27)

The question: “does the neutrino have a proper mass?” is not a correct question: only the pair electron + neutrino has a mass term, and this term is not m but. Neither the neutrino nor the electron have a “proper” mass.

The real part of the invariant wave equation is also: the Lagrangian formalism is a consequence of the wave equation. There is also a conservative current which is now

(28)

We have studied [24] the solutions of our wave equation for electron + neutrino in the case of the hydrogen atom, because this case has made the fame of the Dirac equation. It is astonishing to see that a set of solutions exists, with the same quantum numbers, the same number of states, the same energy levels as for the electron alone. But these solutions are obtained with other potentials:

(29)

where is the fine structure constant. We then have

(30)

And the potentials are obviously a domain where many surprises remain before us. These new solutions of an old problem have a left chirality. We suspect that this left chirality is the origin of the left chirality in bio-che- mistry.

4. The Gauge Group of the Standard Model in Cl_1,5

To get a wave function including electron + neutrino plus two quarks u and d with three states of color each the space-time algebra is not enough: even if the quarks have only left waves these 9 spinor waves (two spinors for the electron) necessitates 36 parameters and if n is equal or greater than 6. We have proved [9] [25] that is enough to get the complete wave as a function of space-time in the Clifford algebra of this extended space-time. We have used previously in [7] a greater space,. But then there was a problem with the generalization of the geometric transformation defined from the wave. This problem comes from the reversion in the extended space-time and it is solved if we use the charge conjugation of the standard model. This charge conjugation divides by 2 the number of parameters, which is equivalent to reduce by one the dimension of the linear space. Then we used which was also. We chose because the calculations were a little simpler.

Three states of “color” are named r, g, b (red, green, blue). So we build a wave with all fermions of the first generation as

(31)

where is defined by (14) and, , are defined on the same model:

(32)

These definitions use the matrix⁸ representation:

(33)

The color is then here only the particular location of a matrix bloc. The wave contains not only all particles of the first generation, but also all anti-particles of these objects. We let

(34)

for The covariant derivative of electro-weak interaction reads now

(35)

We use two projectors satisfying

(36)

Three operators act on the quark sector as on the lepton sector :

(37)

The fourth operator acts differently on the lepton wave and on the quark sector:

(38)

The value −1/3 gives the four correct values of the charges of quarks and antiquarks (see [9] 6.1). To get the gauge group of chromodynamics we need the projectors

(39)

The operators corresponding to the eight generators of read (is abbreviated as c,):

(40)

We can extend the covariant derivative of electro-weak interactions (23):

(41)

where is another constant and are eight terms called “gluons”. Since commute with any element of and since for and each operator

commutes with all operators. Using 12 real numbers, , , we let

(42)

and we get, using exponentiation which is a function from Lie algebra into Lie group (see [9] 6.2):

(43)

The set of these operators is a Lie group. Only difference with the standard model the structure of this group is not postulated but calculated. The gauge invariance reads

(44)

(45)

The group of chromodynamics, generated by the operators projecting the wave on the quark sector acts only on this sector of the wave:

(46)

We get then a gauge group for a wave including all fermions of the first generation. This group acts on the lepton sector only by its part. The physical translation is: leptons do not strongly interact, they have only electromagnetic and weak interactions. This is fully satisfied in experiments. The novelty here is that this comes from the structure itself of the quantum wave.

The wave equation for the complete wave reads:

(47)

The mass term

(48)

contains three defined in (17) and fifteen defined in [9] (B.168) to (B.182) and, , in [9] (B.183) to (B.186). We let now

(49)

Since the only part of the gauge group acts on electron + neutrino the wave equation acts separately in a lepton part and a quark part:

(50)

(51)

The wave Equation (50) is equivalent to

(52)

which is the Equation (18) if we forget that the definition of is changed. The double link between the Lagrangian density and the wave equation exists also for the complete wave Equation (47): the real part of the invariant equation is the sum of the lepton term and the corresponding term for the quark part of the wave equation. This one is equivalent to the invariant form:

(53)

(54)

Like in the lepton case, the real part of the wave equation is simply the equality (see [9] 7.6)

(55)

This link between the wave equation and the Lagrangian density is very strong from the mathematical point of view, since it comes from an algebraic calculation, similar to taking the real part of a complex number. The way going from the Lagrangian density, by the variation calculus and an integration by parts, is on the contrary very dubious from the physical point of view in the case of propagating waves. This method is nevertheless always available from the mathematical point of view. Similarly to (28) only one of the numeric equations equivalent to (53) is simple, the law of conservation of the total current:

(56)

The wave Equation (47) is form invariant under the group defined by (7). The wave satisfies:

(57)

The form invariance of the wave Equation (47) is compatible with the gauge invariance under the group of transformations defined by (44) to (45) (see [25] and [9] B.4 and B.5). This comes from the fact, first pointed by Hestenes [12] that the gauge transformation acts by multiplication on the right place⁹ while geometry acts by multiplication on the left place. The group of gauge invariance is much greater than the group of form invariance, because and M act both by multiplication on the left place. The lepton part and the quark part of the complete wave may be separated, because the lepton part is insensitive to the part of the gauge group. If the quark part is canceled the wave is reduced to the lepton wave (18).

5. Gravitation

Quantum physics was unable to account for gravitation until now because gravitation necessitated a relativistic formulation. And the relativistic part of quantum physics used in the standard model suppressed¹⁰ the mass term of the electron to get the electro-weak gauge invariance. Now we have a relativistic wave equation with mass term able to get the electro-weak and strong interactions from gauge transformations. The mass terms present in our wave equations are able to account for both aspects of the mass: inertial mass and gravitational mass.

5.1. Inertia

Many attempts were developed to reconcile gauge theories and gravitation. General relativity gives the restricted relativity and its Lorentz group as approximation in the case of very low gravity. Since M and R were always confused, since the difference between rotations with or with was always neglected, all these attempts forgot to account for the replacement of by. But this replacement is absolutely necessary since particles with spin 1/2 exist. Now in the preceding section the form invariance was obtained for the R transformations defined from M terms of that were the same for the whole space-time. Such constant M terms produce R dilations which link an inertial frame to another one: the wave equations of quantum mechanics are implicitly written in such inertial frames. An inertial frame is a frame which has no movement of rotation and no acceleration if we compare with very far stars.

We previously considered as an example ( [9] 9.1.1) a frame rotating with the Earth. We let

(58)

And we get

(59)

This gives

(60)

which is the centrifugal acceleration.

Any variable satisfies, in the infinitesimal vicinity of a space-time point x:

(61)

where, are 32 numeric functions of x and are the infinitesimal increments of coordinates. This gives, for:

(62)

Christoffel’s symbols being usually defined as

(63)

this gives

(64)

Only 28 amongst the 32 numeric functions are present in Christoffel’s symbols: the four present in (61) are not in the differential geometry, because the kernel of the group homomorphism is the group generated by i [3] [7] . Einstein had very early the intuition that something was lacking in quantum physics. Effectively the are lacking, not for the spinors of quantum physics, but for vectors and tensors of differential¹¹ geometry: the are present in the term multiplying the spinors of the wave, and are lacking in the transformation of contravariant vectors (63). They are also lacking in the transformation of covariant vectors: we have

(65)

with the same. This gives

(66)

Therefore we get for covariant vectors the usual

(67)

This gives

(68)

where we have let

(69)

This introduces 8 space-time vectors that we name “potentials of inertia”:

(70)

These eight potentials become under a dilation R induced by a constant M

(71)

In space-time algebra we shall need

(72)

And the covariant derivative unifying inertia to gauge interactions becomes

(73)

Contrary to all other terms that contains projectors, the term of inertia acts on the whole wave. This universality is a characteristic of inertia.

5.2. Wave Normalization

One of the differences between classical and quantum wave is the necessity to normalize the quantum wave. In a unified theory we must explain this necessity. Now we know that we always have a Lagrangian density, real part of the invariant wave equation. The invariance of the Lagrangian under all translations, like with the linear Dirac theory, induces the existence of a conservative impulse-energy tensor, the Tetrode’s tensor, which in the case of the electron, for instance, reads:

(74)

Since the wave equation is homogeneous, the Lagrangian is null and we get:

(75)

For a stationary state of an electron with energy E we have:

(76)

So we get:

(77)

The energy of the electron, linked to the frequency of the whole wave, is necessarily equal to the sum of the local energy of the wave, we must then have:

(78)

that is equivalent, for a bound state, to

(79)

This relation was always thought as: is a probability density. We must remark: first was forgotten, because quantum physicists too often used. The precept of the normalization of the wave and the existence of a density of probability are not arbitrary but they are a direct consequence of the principle of equivalence between inertial and gravitational mass-energy, basis of the General Relativity. Finally both the normalization and the density of probability are easy to extend from the case of the lone electron to the wave of electron + neutrino, for the bound states that we have obtained in the case of the hydrogen atom [24] .

5.3. Gravitation

A recurrent problem in the unification of gravitation with the spinor wave of quantum mechanics is the difference of symmetry between the symmetric Ricci tensor of General Relativity and the non-symmetric tensor coming from the spinor wave. At large scales, we can approach differently the momentum-energy tensor: the global energy E of the electron is the temporal component of a space-time vector, the energy-momentum vector. Since the integration has been made in a frame where this momentum is null, this vector reads but it will be seen by other observers moving as. General relativity considers all particles of the universe as giving each such an energy-momentum space-time vector, and if there is no pressure the density of this fluid of particles constitutes the material contribution to the symmetric tensor of energy. Einstein has linked this material tensor to the curvature of the space-time manifold:

(80)

where is the cosmological constant and is the constant of gravitation. We have placed this constant on the left side, then (80) is invariant under. The fermion part of the standard model of quantum physics is therefore compatible with general relativity.

6. The Advantages of This Approach

The use of the three Clifford algebras, and presents many advantages:

We reunite the frame of classical physics, which was the space-time and vectors or tensors built on space-time, with the frame of quantum mechanics, since all interactions are described with real Clifford algebras.

Quantum waves used here are rather similar to the other waves of classical physics: they are well-defined functions of space and time with value in algebras that are also linear spaces on the real field. The quantum wave of the photon is exactly and simply Maxwell’s electromagnetic field (see [9] Sec. 4.4). The relativistic invariance is simply obtained from multiplications on the left place and gauge invariances are obtained from multiplications on the right place.

Since the geometric algebra of the physical space is isomorphic to the complex linear space of matrices (Pauli algebra) the linear spaces of complex functions have invaded quantum physics. Nevertheless this isomorphism is not an isomorphism of complex algebraic structures, but an isomorphism of algebras on the real field. Then complex structures are not fundamental, the true frame of quantum physics is real Clifford algebras. Hermiticity and unitarity are not fundamental: the true conjugation is the reversion, in each algebra (see ( [9] Sec. 6.4) and (18)). Reverse and adjoint are identical in and only there.

Waves, for fermions and antifermions but also for systems of particles (see ( [9] Sec. 5.2) are well defined functions of space and time with value in a real Clifford algebra: we are no more disturbed by the difference between space coordinates and time coordinate coming from the non-relativistic quantum wave of systems.

We integrate in a classical frame all novelties coming from quantum mechanics:

The fermion wave is made of spinors, objects that are part of the geometric algebra, with the peculiarity that they turn on a half angle in a spacial rotation. The fermion wave has value in a linear space which is also an algebra. Each value may have or not an inverse: we have found (see [9] Sec. 6.4 and 7.5) identities justifying the existence of this inverse.

The charge conjugation is a pure quantum transformation that changes only the differential part of the quantum wave (see [9] 3.4).

The group of form invariance accounts for the spin 1/2 and it is then necessarily greater than the Lorentz group. Consequently the fundamental group of invariance of all physical interactions is, group of all invertible elements in the geometric algebra. Physics, computer science and engineering are reunited.

Because there are two inequivalent homomorphisms of in the group of Lorentz dilation there are left and right waves. They change differently in a Lorentz dilation: the physical space is oriented, and this is experimentally well known in weak interactions.

The invariance group is compatible with an oriented space and with an oriented time. It does not create these orientations, it only conserves them.

There are three generations of fermions and four kinds of neutrinos (see [9] Sec. 5.1 and [26] ).

The integration of two quarks in each generation, with three color states each, is made by adding two and only two dimensions to the usual space. This is compatible with the group of invariance in a way that separates automatically the three usual dimensions from the two supplementary dimensions (see [9] Sec. 7.4.1). This enlarged geometric frame allows a wave equation for all particles and antiparticles of each generation. The wave equation is gauge invariant under a gauge group which is exactly the group of the standard model of quantum physics. This group is not postulated but is a consequence of the geometric structure of the enlarged space-time.

The mass term of the wave equation is compatible with the form invariance under that generalizes the relativistic invariance, and it is compatible with the gauge invariance.

We integrate gravitation:

If an inertial frame is heavy enough to include a quantum wave which is stationary in this frame, a double link exists between the wave equation and the Lagrangian density.

Non-inertial frames are frames coming from the use of variable terms in.

The normalization of the wave and the existence of a density of probability are both consequences of the principle of equivalence between inertial and gravitational mass-energy.

After integration on all physical space, the impulse-energy tensor of the quantum wave generates the symmetric tensor of General Relativity.

We comfort the standard model by diminishing the too numerous free parameters:

Only one proper mass can exist in each generation.

The Weinberg-Salam angle has a fixed calculable value [23] . One number gives the four values of charges of quarks and antiquarks, and the value of this number is compulsory [22] [27] .

The value of the electric charge is determined by the existence of magnetic monopoles (see [9] Sec. 8.3.2).

We justify: Three and only three similar generations and a fourth neutrino (see [26] and below).

Three colors for each quark, two quarks and two leptons in each generation.

The value of the electric charge of leptons and quarks.

The existence of the Planck constant (see [9] Sec. 3.3).

The normalization of the wave and the existence of a density of probability.

The insensitivity of leptons to strong interactions.

The strict conservation of the baryonic number, linked to this insensitivity.

The existence of a Lagrangian formalism, treating separately the three generations (see below).

The Pauli principle [27] .

7. Concluding Remarks

The Weinberg-Salam model was unable to account for an electron with a proper mass, because the mass term of the Dirac equation linked the right to the left wave of the electron. But our wave equation has a mass term and is fully gauge invariant. Therefore the complicated mechanism of spontaneous broken symmetry needed to recover a mass term is useless.

The Higgs boson exists, but it shall not give a way to compute the proper mass of the different fermions. Moreover it is possible that each generation has one Higgs boson.

The relativistic quantum theory was based on the invariance under the Poincaré group. This group contains the translations and all Lorentz transformations, conserving or not space and time orientation. In this frame the proper mass is the fundamental invariant.

On the contrary the group of Lorentz dilations contains only the subgroup of Lorentz transformations conserving, separately, the space orientation and the time orientation. The Poincaré group is both too great and too small: it is too great, because P and T transformations are purely theoretical, they are impossible to realize in the physical world.

And it is too small, because it does not account for the spin 1/2 and the dilations induced by any M of. Contrary to the axiomatic quantum theory, the proper mass is then not the fundamental invariant, it is which is fundamental.

The existence of three and only three generations of fermions comes from the existence of a privileged third direction in the wave Equation (47) and also in the linear Dirac equation [9] . We get two and only two similar equations:

(81)

The first one has a privileged first direction and the second has a privileged second direction. The privileged direction is the direction where the spin is always measured. The operator, which contains the differential and gauge terms, changes also from one generation to another, and the mass term also. For instance the projectors on right and left waves are replaced by in the first Equation (81) and by in the second Equation (81). We must also replace the used to get the charge conjugate in (14) respectively by and with (81), and so on. Then we get a Lagrangian density for the first Equation (81) and another one for the second equation, which are the real parts of the respective equations. This explains why three separated Lagrangian densities are used in the standard model for electro-weak interactions. This process of change acts only on the electro-weak operators and does not change the operators used in chromodynamics. The neutrino part of each lepton wave does not change its place in the global wave, from one generation to the following, and then may interact with the charged lepton of each generation. Nevertheless each neutrino wave is specific to one generation, since the neutrino has only a left wave, defined by a projector which changes with the generation. The possibility of a fourth neutrino [26] comes from the existence of four independent terms with square-1 in.

Several theoretical attempts beyond the standard model were studied. The “great unified” theories used a compact Lie group like or to include the gauge group of the standard model. Since this group comes from the structure of the wave, there is no geometrical reason to get a greater group. This implies that we have no reason to expect new fermions coming from a fourth generation, no new gauge bosons coming from a greater gauge group. Magnetic monopoles are then the last domain of particle physics that remains to study (see [9] Chapter 8 and [22] ).

The principal results of the standard model of quantum physics come from the first quantization, not from the second quantization of the quantum field theory which appears successful only for electromagnetic laws, only for the electric gauge.

Most of our results are about fermions. The boson part of the quantum world has been nevertheless not completely neglected. We have transposed in Clifford algebra the construction of the wave of a system of electrons by antisymmetric product (see [9] Sec. 5.2) and (see [9] Chapter 4) the De Broglie’s theory of light [28] [29] . This theory of light is a beginning for the wave equations of the twelve bosons of the standard model, the interactions between fermions and bosons and between bosons. A construction is possible from the fermion wave to build the wave of all other objects of the quantum world by antisymmetric products. An even number of waves gives a boson, an odd number gives a fermion. This is completely different from the supersymmetry, a theory based on the transformation of fermions into bosons and vice versa. Such a transformation is impossible if the boson or fermion nature of the wave comes from the even or odd number of fundamental fermions building this wave.

The De Broglie’s construction gives the classical electromagnetic field and Maxwell’s laws, therefore it appears as a better method to build boson waves. This construction, based on the linear Dirac equation, had the same difficulty than the Weinberg-Salam model with the mass term, which was incompatible with the gauge. We can hope now, with a mass term compatible with the gauge group, a new departure [30] for De Broglie’s method of fusion.

Since all electromagnetic laws and also the gravitation use only, simplest of the three algebras, the next step (in preparation) will be the description of the four interactions in this frame.

Cite this paper

Claude Daviau,Jacques Bertrand, (2016) Three Clifford Algebras for Four Kinds of Interactions. Journal of Modern Physics,07,936-951. doi: 10.4236/jmp.2016.79086

References

NOTES

¹This link is important and non trivial. The matrices of the Dirac theory are defined only up a unitary matrix. Studying the electron, D. Hestenes [11] - [13] , A. Lasenby [14] , C. Doran [15] and one of us [16] , we have implicitly used the set of Dirac matrices coming from the non relativistic Pauli equation. Another set is used for the relativistic electron, the Weinberg-Salam model and the theory of Lochak’s magnetic monopole [17] - [19] . These matrices are linked to the left and right Weyl spinors.

²The proper mass m and are invariant under, covering group replacing the awaited Lorentz group of special relativity, but the Nature uses a greater strain, the true group of invariance of physical laws is not but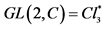. Consequently only the product remains invariant under the full group.

³This means that the orientation of space and the orientation of time are both conserved in any Lorentz dilation.

⁴The Lagrangian density is null for any solution of the Lagrange equations because the wave equation is homogeneous. This property results from the Noether’s theorem.

⁵The knowledge of the reason for the existence of the extremum principle is obviously an important result.

⁶The complete wave, with and, describes the magnetic monopole found by Lochak [17] - [19] [22] .

⁷Only 16 of these densities were known from the Dirac matrix theory.

⁸We use three Clifford algebras which are also matrix algebras. This has been sometimes not very well considered. So it is necessary to remark: first it is not the structure of complex matrices which is used, but the structure of algebra on the real field. Next most complex matrix algebras are not Clifford algebras, and we use only with. In these three cases the Clifford product is the matrix product. So we use the product with blocs as help for the computation of the Clifford product. We use the determinant of the matrix which tells us if the matrix has an inverse or not.

⁹This is not completely true because acts on the left place in.

¹⁰The weak gauge necessitates a distinction between the left and the right wave of the electron. And the linear mass term of the Dirac equation links these two parts of the wave. The suppression of the mass term was a necessity, justified from the physical point of view by the very small mass of the electron in comparison with the huge masses of W and bosons.

¹¹Many attempts have been made to describe by means of differential geometry the quantum world. Since the methods of differential geometry are local, they use easily infinitesimal transformations. And these infinitesimal transformations act in the Lie algebra of the studied group of transformations: it is then easy to do not see the difficulty: the group of the M and the group of the R are very different groups. The distinction between the rotation of the wave, with a q angle, and the rotation of the space, with a 2q angle, is compulsory to build a quantum theory including geometry.