International Journal of Modern Nonlinear Theory and Application
Vol.2 No.4(2013), Article ID:40325,3 pages DOI:10.4236/ijmnta.2013.24033
Global Estimation of the Cauchy Problem Solutions’ Fourier Transform Derivatives for the Navier-Stokes Equation
Buketov Karaganda State University, Karaganda, Kazakhstan
Email: aset.durmagambetov@gmail.com
Copyright © 2013 Asset A. Durmagambetov, Leyla S. Fazylova. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received September 19, 2013; revised October 19, 2013; accepted October 25, 2013
Keywords: Fourier Transform; Cauchy Problem; Navier-Stokes Equations
ABSTRACT
The uniform estimation of the derivatives of Fourier transforms of the Cauchy problem for the Navier-Stokes equations was obtained.
1. Introduction
Numerous studies of the Navier-Stokes equations are devoted to the problem of its solution’s smoothness. A good overview of the studies was made in [1,2]. Spatial differentiability of the solutions is one of the most important aspect of the study, as it is mostly responsible for an evolution of the solutions.
Obviously differentiable solutions do not provide an effective description of turbulence. On the other hand, the global solvability and differentiability of the solutions are not proven, and therefore the turbulence description problem remains to be open.
It is interesting to study the properties of the Fourier transform of solutions of the Navier-Stokes equation: how they can be used in the description of turbulence, and whether they are differentiable. Differentiability of Fourier transform of the Navier-Stokes equation’s solution seems to be related to the appearance or disappearance of the resonances, as it will mean the absence of large energy flows from small to large harmonics, which in turn means the inability of turbulence.
Thus, obtaining the uniform global estimations of the Fourier transform of solutions of the Navier-Stokes equations will mean that the principle of modeling of complex flows and related calculations shall be based on the Fourier transform method.
The authors continue to research these issues in application to the numerical weather prediction model and this paper is a theoretical justification for this approach.
2. Cauchy Problem for the Navier-Stokes Equation
Consider Cauchy problem for the Navier-Stokes equations:
 (1)
(1)
 (2)
(2)
in the domain , supposing about
, supposing about :
:
 (3)
(3)
The problem (1), (2), (3) has at least one weak solution  in the so-called Leray-Hopf class [1].
in the so-called Leray-Hopf class [1].
Here are the known results proved in [1]:
Theorem 1 If
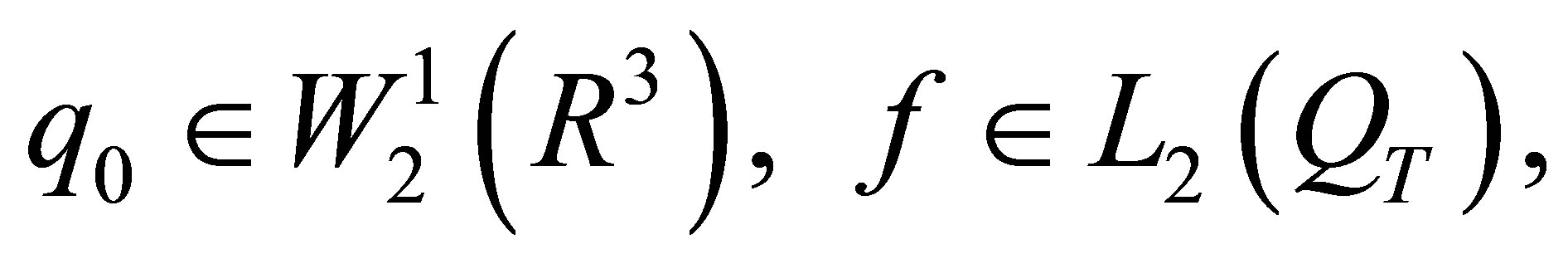 (4)
(4)
there is a single generalized solution of (1), (2), (3) in the domain ,
,  , satisfying to the following conditions:
, satisfying to the following conditions:
 (5)
(5)
Note that  depends on
depends on ,
, .
.
Lemma 1 Let ,
,  , then
, then
 (6)
(6)
Our goal is to provide global estimatimation of Fourier transforms of the Navier-Stokes equations’ soutions derivatives (1), (2), (3) without assumption of the smallness of the initial velocity and force.
We get this time-uniform estimation. Let use the following notation:
 (7)
(7)
 (8)
(8)
Assertion 1 The solution of (1), (2), (3) according to the Theorem 1 staisfies to:
 (9)
(9)
where .
.
This follows from the definition of the Fourier transform and the theory of linear differential equations.
Assertion 2 The solution of (1), (2), (3) staisfies to:
 ` (10)
` (10)
and the following estimations:
 (11)
(11)
 (12)
(12)
Submission for  obtained by using
obtained by using  and the Fourier transform. The estimations follow from this representation.
and the Fourier transform. The estimations follow from this representation.
Lemma 2 The solution of (1), (2), (3) in Theorem 1 satisfies to the following inequalities:
 (13)
(13)
 (14)
(14)
or
 (15)
(15)
 (16)
(16)
This follows from the Navier-Stokes equations, first a priori estimation (Lemma 1) and Lemma 2.
Lemma 3 The solution of (1), (2), (3) satisfies to the following inequalities:
 (17)
(17)
 (18)
(18)
 (19)
(19)
These estimations follow from (9), Parseval’s identity, Cauchy-Schwarz inequality, Lemma 3.
Lemma 4 The solution of (1), (2), (3) satisfies to the following inequalities:
 (20)
(20)
where  are finite.
are finite.
Let prove the first estimation. By definition of  and Lemm 3,4 assertions follow the inequlities:
and Lemm 3,4 assertions follow the inequlities:
 (21)
(21)
where .
.
The rest estimations can be proved in a similar way.
Lemma 5 The solution of (1), (2), (3) according to the Theorem 1 staisfies to:  where:
where:
 (22)
(22)
This follows from a priori estimation (Lemma 1) and assertion of Lemma 3.
Lemma 6 Let ,
,  , then:
, then:
 (23)
(23)
Provement of the lemma can be obtained using Plancherel theorem.
3. Conclusion
Thus, the uniform global estimations of the Fourier transform of solutions of the Navier-Stokes equations indicate that the principle of modeling of complex flows and related calculations shall be based on the Fourier transform method. In terms of the Fourier transform, both smooth initial conditions and right-hand sides do not appear exacerbations modes for speed and pressure. Loss of smoothness in terms of the Fourier transform can be expected only in the case of singular initial conditions, or of unlimited forces in the .
.
4. Acknowledgements
We thank the Ministry of Education and Science of the Republic of Kazakhstan for a grant, and the “Factor” Company of System Researches for combining our efforts in this project.
The work was performed as part of the international project “Joint Kazakh-Indian study the influence of anthropogenic factors on atmospheric phenomena on the basis of numerical weather prediction models WRF (Weather Research and Forecasting)”, commissioned by the Ministry of Education and Science of the Republic of Kazakhstan.
REFERENCES
- O. A. Ladyzhenskaya, “Mathematic Problems of Viscous Incondensable Liquid Dynamics,” M.: Science, 1970, p. 288
- V. A. Solonnikov, “Estimates Solving Nonstationary Linearized Systems of Navier-Stokes’ Equations,” Transactions Academy of Sciences USSR, Vol. 70, 1964. pp. 213- 317.

