Journal of High Energy Physics, Gravitation and Cosmology
Vol.03 No.02(2017), Article ID:74983,10 pages
10.4236/jhepgc.2017.32022
Quantum Neutron Unit Gravity
Donald Chakeres1, Vola Andrianarijaona2
1Department of Radiology, The Ohio State University, Columbus, OH, USA
2Department of Physics and Engineering, Pacific Union College, Angwin, CA, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 28, 2017; Accepted: March 26, 2017; Published: March 29, 2017
ABSTRACT
Quantum gravity and the transformation of a neutron star or the merger of two neutron stars into a black hole are important topics in cosmology. According to the Schwarzschild radius relationship, a black hole arises when two times of the gravitational binding energy of the gravitational system, GBE, equal the annihilation energy of its total mass. From a quantum perspective, the integer number of neutrons defines the GBE and mass in the merger of binary pure neutron stars transforming to a black hole. Therefore, one can scale all gravitational binding energy relationships by using neutron mass, energy, distance, time, or frequency equivalents. We define 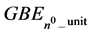 of the neutron as the binding energy, 1.4188 × 10−49 J, of a virtual system of two neutrons separated by the neutron Compton wavelength. The
of the neutron as the binding energy, 1.4188 × 10−49 J, of a virtual system of two neutrons separated by the neutron Compton wavelength. The 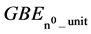 divided by a neutron’s rest mass energy represents a fundamental, dimensionless proportionality constant, 9.4252 × 10−40,
divided by a neutron’s rest mass energy represents a fundamental, dimensionless proportionality constant, 9.4252 × 10−40,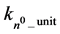 . The square root of
. The square root of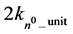 ,
, 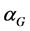 , which we introduce here as a coupling constant, is identical in concept to the fine structure constant found in electromagnetic physics, but for gravity. Both αG and
, which we introduce here as a coupling constant, is identical in concept to the fine structure constant found in electromagnetic physics, but for gravity. Both αG and 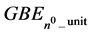 inter-relate the neutron, proton, electron, Bohr radius, speed of light, Planck’s constant, GBE of the electron in hydrogen, and Planck time. This paper demonstrates a direct conceptual and computational rationale of why the neutron and its negative beta decay quantum products accurately can represent a quantum gravitational natural unit system.
inter-relate the neutron, proton, electron, Bohr radius, speed of light, Planck’s constant, GBE of the electron in hydrogen, and Planck time. This paper demonstrates a direct conceptual and computational rationale of why the neutron and its negative beta decay quantum products accurately can represent a quantum gravitational natural unit system.
Keywords:
Quantum Gravity, Neutron, Black Holes, Neutron Stars

1. Introduction
Developing a quantum model of gravity has been an important conceptual goal in physics [1] - [6] . Uniting cosmologic physics and quantum physics is a continuing incomplete process. Many different models have been proposed, but none have seamlessly united quantum, classical and cosmologic phenomena [7] . Neutron, n0, neutron stars, NS, and black holes, BH, are ideal conceptual, computational, and observational settings to interrogate gravitational properties at the extremes of short and long distances, and high gravitational binding energies, GBEs [8] - [14] . Many new observations are being acquired that lend themselves to interpretations of the basic properties and scaling of gravitational systems. Recent gravity wave measurements are dependent upon a robust gravity model [15] [16] .
A NS is related to the transformation of atomic matter, in the simplest case hydrogen, H, to a degenerate n0 state driven by gravity. NSs can be characterized by a few physical factors since they are composed predominately of neutrons, and these are referred to as equations of state [17] [18] . Some theoretical studies consider NSs as pure n0 matter [19] . Some models describe the core as superfluid neutron-degenerate matter (mostly neutrons, with some protons and electrons). About 5% of all known NSs are in binary systems [20] . In some theories of binary evolution it is expected that NSs also exist in binary systems with a BH. It has been proposed that coalescence of binaries consisting of two NSs may be responsible for producing short gamma-ray bursts [21] .
A BH is a mathematically defined region of spacetime exhibiting such a powerful gravitational force that no particle or electromagnetic radiation can escape. The classic Schwarzschild radius equation states that a BH arises when the annihilation energy of the total mass with a Schwarzschild radius of rs, (massBH_rs)c2 in joules, equals two times GBE in joules for any BH horizon measuring rs (see Equation (1) and Equation (2)). From a quantum perspective of a pure binary NS system transformation to a BH, Equation (2) is a mathematical imperative expressing the equivalence between the integer number of neutrons defining the annihilation mass and the paired masses defining the GBE [22] [23] .
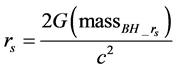 (1a)
(1a)
or
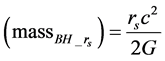 (1b)
(1b)
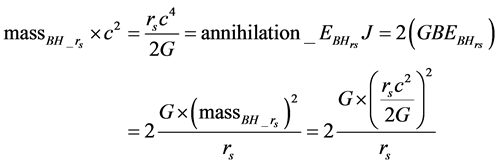 (2)
(2)
This is a specialized physical/mathematical setting where two entities, annihilation energy of a mass and a different form of energy, two times of the binding energy in this case, must be identically scaled in a paired relationship. It leads to a dimensionless quantum number of neutrons relationship defining both simultaneously. Another similar physical single and paired example would be related to matter/anti-matter pair production which is also important in the properties of BHs [24] . In pair product there are photon and two anti-particles in which the total energies are scaled equally. In anti-matter matter annihilation there are two matter entities and two photons. The number 2 reflects the paired physical state relationship. Both are associated with physical transformation settings where the velocity of matter is related to the speed of light, c, and the annihilation energy of the rest mass, mc2. In the transformation of a binary system of NSs to a BH, the GBE scaling can be defined equivalently and solely in integer multiples of the energy of n0, equaling 1.5053 × 10−10 J, which is a natural energy unit. This energy unit could be also expressed in term of its equivalent in frequency, 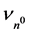 , (by dividing the energy by Planck’s constant h) or in terms of n0 Compton wavelength,
, (by dividing the energy by Planck’s constant h) or in terms of n0 Compton wavelength,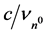 . Therefore gravity can be scaled as a single natural unit system that is inter-related by integer multiples or integer fractions of n0 units.
. Therefore gravity can be scaled as a single natural unit system that is inter-related by integer multiples or integer fractions of n0 units.
The goal of this paper is to evaluate the specific units from a quantum integer perspective of a natural scaling based solely on the neutron, which define a system of gravity that is conceptually and computationally consistent with standard gravitation models and methods for NSs and BHs.
2. Virtual Neutron Gravity Energy Unit, GBEn0_unit
We define the simplest virtual n0 based natural unit gravitational system, GBEn0_unit, as the GBE of virtual paired n0 masses separated by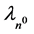 , a distance that is equal to the speed of light divided by the annihilation frequency of the neutron,
, a distance that is equal to the speed of light divided by the annihilation frequency of the neutron,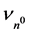 . The GBE in Joules of this system, GBE n0_unit J, 1.4188 × 10−49 J, is described in Equation (3).
. The GBE in Joules of this system, GBE n0_unit J, 1.4188 × 10−49 J, is described in Equation (3).
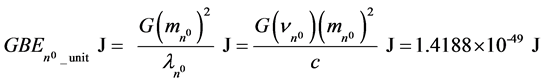 (3)
(3)
Here, 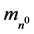 denotes the mass of the neutron, 1.6749 × 10−27 kg, G, the universal Newtonian gravitational constant, and c the speed of light. vn0 represents the frequency equivalent of the neutron, 2.2719 × 1023 Hz,
denotes the mass of the neutron, 1.6749 × 10−27 kg, G, the universal Newtonian gravitational constant, and c the speed of light. vn0 represents the frequency equivalent of the neutron, 2.2719 × 1023 Hz,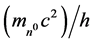 .
. 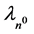 is the n0 Compton wavelength 1.3196 × 10−15 m.
is the n0 Compton wavelength 1.3196 × 10−15 m. 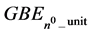 values in other physical unit equivalents include frequency 2.1413 × 10−16 Hz (
values in other physical unit equivalents include frequency 2.1413 × 10−16 Hz (
3. Virtual Neutron Gravity Dimensionless Coupling Proportionality Constant Unit, kn0_unit
GBEn0_unit J is related to a proposed dimensionless coupling proportionality constant ratio with the n0_unit in J, with 




4. kn0_unit, Planck Time, and Hydrogen
Our proportionality constant, kn0_unit is also defined by several equivalent relationships involving GBEn0_unit; Planck’s constant, h; Planck time, tP; and the frequency equivalents of the neutron, proton (p+), electron (e−), Bohr radius (a0), and GBE of the electron in hydrogen; respectively vn0, vp+, ve−, 






From Equation (5) the ratio of vGBE_n0_unit divided by vGBE_e− is related to the ratio of quantum entities of 


5. Proposal of a Gravitational Constant Analogous of the Fine Structure Constant, αG
We also find interest in computing the square root of


The kinetic energy of this virtual n0-system is the mass of n0 times the product of (αG × c) squared divided by 2. This equals



The mathematical connection with the closest natural atomic system, which represents hydrogen, shows that vGBE_e is a fundamental constant with similar importance to quantum gravity, and is analogous to the significance of the electromagnetic binding energy of the electron in H to photon and electromagnetic systems. This constant cannot be measured, but it does not diminish its physical significant. In fact, the Bohr radius, rest mass of the electron, and the Rydberg constant that define the hydrogen quanta cannot be experimentally measured either. This fundamental frequency vGBE_e− equals, 2.9000 × 10−24 Hz; equivalently 2.1381 × 10−74 kg; 1.0337 × 1032 m; or 1.9216 × 10−57 J. The product of 





The value of αG equals the product of square root of 2, 

6. Definition of the Newtonian Gravitation Constant in Neutron Units
As an added and quite surprising result the Newtonian gravitational constant G can be completely defined in the defined units of the n0 mass, its Compton wavelength, its unit GBE; or with c and neutron frequency equivalent as in Equation (9).

Equivalently, the Newtonian gravitational constant G can also be defined in units of n0, c, h, tP, vp+, ve−, va0, vGBE_e−,and neutron beta decay products in H as shown in Equation (10). This is analogous to the inter-relationship of multiple fundamental quantum constants that can define a0 or α.

7. Gravitational Binding Energy of Any System from an Integer Neutron Perspective
The GBE can be calculated for any system using the integer unit n0 perspective by Equation (11). 


8. An Example of the Transition of a Symmetric Binary Pure Neutron NS System to a BH
Consequently we have just established the transformation of binary symmetric NSs of identical mass, merging into a BH as in Figure 1. rs is arbitrarily chosen to be c × s for mathematical simplicity, and it is a fundamental unit distance linked to all of the other constants. A Schwarzschild radius, rs, of c × s equals 299,792,458 m is utilized to demonstrate a relevant cosmological dimension in the Schwarzschild ratios shown in Equation (12). The mass of such a BH equals the product of c2 times c × s divided by the product of 2 times the gravitational
Figure 1. Transformation of a symmetric binary neutron star system to a black hole. Figure 1 is a plot showing the transformation of the binary symmetric neutron system to a black hole with a Schwarzschild radius of c × s. The X-axis is log10 # of n0. The Y-axis is in log10 Joules of the annihilation energy of the # of n0, the upper blue line; and 2 times the gravitational binding energy, GBE, of a system with # of n0 separated at a distance of c × s, the lower green line, Equation (2). The far left side of the plot begins at a binary single n0 system. To the right the integer number of n0 of each component of the pair increases towards 1.2051 × 1062 neutrons. At that specific # of n0, red circle, 2 times the GBE and the annihilation energy of the mass are equal leading to the transformation to a BH.
constant G, which computes to a total mass of 2.0186 × 1035 kg from Equation (12). This is described as



The factor 2 is taken into account in these calculations to define the point of transition of the binary n0 masses to a BH. Since the GBE increases with the square of the number of n0 there is a point where the two lines and energy values converge, Figure 1. This is the transformation point to a BH. At neutron star pairing with a mass of 2.0185 × 1035 kg 2 times the GBE equals the annihilation energy of the mass fulfilling the mathematical definition of a BH, Equations ((2), (13)). This demonstrates that binary gravitational systems from any pairing of two neutrons, two stars, and two NS, and one BH can be described by a quantum n0-based system.
9. Discussion
These results show how gravitation systems, indeed the Newtonian Gravitational constant itself, can be completely scaled by a quantum or n0-unit system (see Equations ((9)-(11)).) This is an imperative of the mathematical definitions of pure NSs transforming to simplest non-rotating BHs. The GBE of any system represents dimensionless integer fractional values of the neutron as the base unit, which provides dimensionless ratio coupling constants defined by kn0_unit and αG. Surprisingly, these are related to quantum subatomic constants derived from the frequency equivalents of the neutron, hydrogen, and tP, (Equation (10)). This demonstrates a system that bridges from quantum to gravitational. Similarly both α and αG represent conceptually and computational parallel β values, but are relegated to widely divergent physical settings. The fine structure constant α relates to electromagnetic relationships of hydrogen, whereas αG is for neutron gravitational relationships. The electromagnetic binding energy of the electron in hydrogen, related to the Rydberg constant, is a fundamental scaling factor for all electromagnetic relationships including α. The GBE of the electron in hydrogen plays an identical role for neutron quantum gravity. Though our derived GBE_e-value is not directly observable it still represents an important fundamental inter-relational constant identical in concept to the other hydrogen quanta.
The time and distance units of gravity may also be defined by n0-equivalents. The time unit is one second divided by



10. Conclusions
In conclusion, mathematical definitions of pure Neutron Stars and Black Holes define an imperative that the scaling of the gravitational binding energy must be defined in quantum unit equivalents of the neutron. The dimensionless ratios, kn0_unit and αG, of a pure neutron gravitational system, are defined by four quantum entities, and the n0, the speed of light, the products of negative n0 beta decay, p+, e−, a0, vGBE_e−, as in Equations ((5), (7)). Newton’s Gravitational constant G, can be defined solely in n0-units and/or the speed of light, tP, and hydrogen quantum values as in Equations ((9), (10)). Therefore gravity can be viewed as being scaled by the neutron which is an imperative in the NS BH transition. Time (chronon), matter (second quantization), distance (Planck scales), and energy (Rydberg spacing) also must be quantum integer based on n0. Since all of the dimensions of a gravitational system are scaled by a single natural unit, the neutron, the system can be computationally analyzed as dimensionless inter-re- lationships just as electromagnetic systems are with the fine structure constant as in Equation (11).
Acknowledgements
We would like to thank Richard Vento, Columbus State Community College― retired for his help in the preparation of the paper.
Cite this paper
Chakeres, D. and Andrianarijaona, V. (2017) Quantum Neutron Unit Gravity. Journal of High Energy Physics, Gravitation and Cosmology, 3, 267-276. https://doi.org/10.4236/jhepgc.2017.32022
References
- 1. Ashtekar, A., Baez, J., Corichi, A. and Krasnov, K. (1998) Quantum Geometry and Black Hole Entropy. Physical Review Letters, 80, 904-907.
https://doi.org/10.1103/PhysRevLett.80.904 - 2. Padmanabhan, T. (1998) Quantum Structure of Spacetime and Blackhole Entropy. Physical Review Letters, 81, 4297-4300.
https://doi.org/10.1103/PhysRevLett.81.4297 - 3. Husain, V. and Pawlowski, T. (2012) Time and a Physical Hamiltonian for Quantum Gravity. Physical Review Letters, 108, Article ID: 141301.
https://doi.org/10.1103/PhysRevLett.108.141301 - 4. Marshakov, A. (2009) Two-Dimensional Quantum Gravity and Quasiclassical Integrable Hierarchies. Journal of Physics A: Mathematical and Theoretical, 42, Article ID: 304021.
- 5. Reuter, M. and Schwindt, J.M. (2007) Scale-Dependent Metric and Minimal Length in QEG. Journal of Physics A: Mathematical and Theoretical, 40, 6595-6605.
https://doi.org/10.1088/1751-8113/40/25/S04 - 6. Oriti, D., Pereira, R. and Sindoni, L. (2012) Coherent States in Quantum Gravity: A Construction Based on the Flux Representation of Loop Quantum Gravity. Journal of Physics A: Mathematical and Theoretical, 45, Article ID: 244004.
- 7. Lykken, J. and Spiropulu, M. (2014) Supersymmetry and the Crisis in Physics. Scientific American, 310, 34-39.
https://doi.org/10.1038/scientificamerican0514-34 - 8. Gürlebeck, N. (2015) No-Hair Theorem for Black Holes in Astrophysical Environments. Physical Review Letters, 114, Article ID: 151102.
https://doi.org/10.1103/PhysRevLett.114.151102 - 9. Pasham, D.R., Strohmayer, T.E. and Mushotzky, R.F. (2013) Discovery of a 7 mHz X-Ray Quasi-Periodic Oscillation from the Most Massive Stellar-Mass Black Hole IC 10 X-1. The Astrophysical Journal Letters, 771, Article ID: L44.
- 10. Agulló, I., Barbero, G.J., Díaz-Polo, J., Fernández-Borja, E. and Villaseño, E. (2008) Black Hole State Counting in LQG: A Number Theoretical Approach. Physical Review Letters, 100, Article ID: 211301.
https://doi.org/10.1103/PhysRevLett.100.211301 - 11. Ammon, M., Gutperle, M., Kraus, P. and Perlmutter, E. (2013) Black Holes in Three Dimensional Higher Spin Gravity: A Review. Journal of Physics A: Mathematical and Theoretical, 46, Article ID: 214001.
- 12. Bailin, D., Green, R.J. and Love, S. (1979) The Superfluid Phase Transition in Neutron Star Matter. Journal of Physics A: Mathematical and General, 12, 6.
https://doi.org/10.1088/0305-4470/12/6/004 - 13. Durgapal, M.C., Rawat, P.S. and Bannerji, R. (1980) Structures with Extreme Relativistic Cores. Journal of Physics A: Mathematical and General, 13, 3761-3768.
https://doi.org/10.1088/0305-4470/13/12/025 - 14. Durgapal, M.C., Pande, A.K. and Pandey, K. (1979) Isothermal Neutron Star Core. Journal of Physics A: Mathematical and General, 12, 6.
https://doi.org/10.1088/0305-4470/12/6/016 - 15. Favata, M. (2014) Systematic Parameter Errors in Inspiraling Neutron Star Binaries. Physical Review Letters, 112, Article ID: 101101.
https://doi.org/10.1103/PhysRevLett.112.101101 - 16. Abbott, B.P., et al. (LIGO Scientific Collaboration and Virgo Collaboration) (2016) GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence. Physical Review Letters, 116, Article ID: 241103.
https://doi.org/10.1103/physrevlett.116.241103 - 17. Prakash, M., Ainsworth, T.L. and Lattimer, J.M. (1988) Equation of State and the Maximum Mass of Neutron Stars. Physical Review Letters, 61, 2518.
https://doi.org/10.1103/PhysRevLett.61.2518 - 18. Takami, K., Rezzolla, L. and Baiotti, L. (2014) Constraining the Equation of State of Neutron Stars from Binary Mergers. Physical Review Letters, 113, Article ID: 091104.
https://doi.org/10.1103/PhysRevLett.113.091104 - 19. Lattimer, J.M. (2012) Constraints on Neutron Star Radii. Annual Review of Nuclear and Particle Science, 62, 485-515.
https://doi.org/10.1146/annurev-nucl-102711-095018 - 20. Baumgarte, T.W., Cook, G.B., Scheel, M.A., Shapiro, S.L. and Teukolsky, S.A. (1997) Binary Neutron Stars in General Relativity: Quasi-Equilibrium Models. Physical Review Letters, 79, 1182-1185.
https://doi.org/10.1103/PhysRevLett.79.1182 - 21. Dubus, G. (2008) High Energy Gamma-Ray Emission from Binaries. New Astronomy Reviews, 51, 778-784.
- 22. Morales-Técotl, H.A. and Rovelli, C. (1994) Fermions in Quantum Gravity. Physical Review Letters, 72, 3642-3645.
https://doi.org/10.1103/PhysRevLett.72.3642 - 23. Casals, M. and Ottewill, A. (2012) Spectroscopy of the Schwarzschild Black Hole at Arbitrary Frequencies. Physical Review Letters, 109, Article ID: 111101.
https://doi.org/10.1103/PhysRevLett.109.111101 - 24. Hawking, S.W. and Ross, S.F. (1995) Pair Production of Black Holes on Cosmic Strings. Physical Review Letters, 75, 3382-3385.
https://doi.org/10.1103/PhysRevLett.75.3382


