Received 2 April 2016; accepted 23 May 2016; published 26 May 2016

ABSTRACT

Malaria infection is a major problem in many countries. The use of the Insecticide-Treated Bed- Nets (ITNs) has been shown to significantly reduce the number of malaria infections; however, the effectiveness is often jeopardized by improper handling or human behavior such as inconsistent usage. In this paper, we present a game-theoretical model for ITN usage in communities with malaria infections. We show that it is in the individual’s self interest to use the ITNs as long as the malaria is present in the community. Such an optimal ITN usage will significantly decrease the malaria prevalence and under some conditions may even lead to complete eradication of the disease.

Keywords:

Game Theory, Malaria Prevention, Optimal Strategy, Epidemic Modelling, SIS Model

1. Introduction

Malaria is a vector born disease that can be transmitted to people through mosquito bites, prevalent in tropical and subtropical regions of the world. The World Health Organisation estimates that every year nearly one million people die as a result of malaria [1] . A lot of effort has been put into treatment and prevention strategies, and an ambitious goal of organisations such as the World Health Organisation and the Bill and Melinda Gates foundation is the complete elimination of malaria.

One of the key methods of malaria prevention is the use of Insecticide-Treated Bed-Nets (ITNs) that kill and also repel mosquitoes [2] . [3] found that the use of ITNs can reduce malaria cases by 50% and death in children by 20%. The use of ITNs was demonstrated to be very cost-effective, see e.g. [4] - [6] . This is important given both the scale of the problem (about 200 million people are at a very high risk [7] ), and the fact that most of the areas of high malaria prevalence are relatively poor. However, human behavior such as inconsistent usage due to hot weather diminishes the effectiveness of the ITNs.

The impact of ITN usage on the spread of the malaria infection has been recently studied in a series of mathematical models such as [8] - [10] . In particular, [10] developed an ODE model for the effects of ITN on the malaria transmission dynamics and called for a better understanding of the impact of human behavior on the usage.

Game theory is a well suited tool to study human behavior in a quantitative way [11] . Starting by [12] , game theory has been long used in biology [13] , and [14] used it to study vaccination decisions in situation where individuals face a potentially costly preventive action (such as to use an ITN) that can reduce a risk of con- tracting the disease. Game theory has been applied to vaccination against major public health threats [15] - [21] and it is particularly useful because the outcome of the individual decision (to vaccinate or to use an ITN) depends on the decisions of other members of the population because the overall vaccination or ITN usage yields the disease prevalence in the community [22] .

In particular, game theoretical models can be used to understand why in many cases disease eradication can be very hard [14] even when the cost of preventive action is very low [23] . There is often a great incentive to use preventative measures when a disease is at high levels, but when brought below a certain level the incremental benefit of taking the presentative action declines, and so individuals have less incentive to use it. Thus pre- vention can sometimes (but not always) become ineffective before total eradication occurs. In this paper we adapt a non-game theoretical model of ITN usage [10] to study the impact of individual decisions on the effectiveness of ITN usage.

2. The Model

2.1. Model of Malaria Transmission

We will use the basic model for the transmission dynamics of malaria infection as presented in [10] . The host population (humans) is divided into two compartments (susceptible and infectious), which are denoted by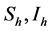, respectively. A total host population is given by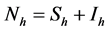. The vector population (mosquitoes) is also divided into two compartments (susceptible and infectious) which are denoted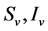, respectively. The total vector population is given by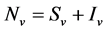. When a mosquito bites a human, the susceptible human is infected by an infected mosquito with probability 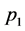and a susceptible mosquito is infected by an infected human with probability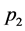. Hosts die with natural mortality rates being 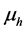and can also die because of malaria with rate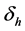. Hosts recover with rate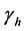. Vectors can die with rate

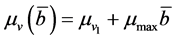(1)

where 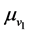is the natural mortality rate of hosts and 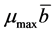is the mortality rate due to ITN use in the population. Here, 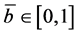denotes the average ITN usage in the population. Each individual chooses its own individual ITN usage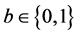. We assume that all individuals are born as susceptible (with recruitment rates and respectively) and no infected individuals come from outside. All parameters and their values are summarized in Table 1.

Let be the force of infection for the focal susceptible host. [10] give the formula

(2)

where is the transmission probability per bite from infectious mosquitoes to humans, is the average

number of bites per mosquito per unit of time, is the average number of mosquitoes per host, and thus

is the average number of bites a susceptible host gets per unit time, and finally is the

proportion of infectious mosquitoes. [10] considers

(3)

with and which yields and (i.e. ITNs provide complete pro- tection).

Also, the average force of the infection is

(4)

and thus

(5)

In the state when malaria reaches equilibrium, [10] evaluates as a solution to

(6)

where

(7)

(8)

(9)

(10)

(11)

In [10] it is shown that there are potentially two stable steady states of infections and if the malaria was originally common, the stable states yields

(12)

Figure 1 shows values of for specific parameter values. Note that eventually becomes 0 (quite abruptly as seen in Figure 1(a)) as increases. This is caused by the fact that for large, the disease can be eradicated according to the model presented in [10] .

2.2. Game-Theoretical Model

Let be the payoff for a focal individual using () or not using () the ITN in a population where the average use of ITNs is. We shall find the ITN usage equilibrium usage level satisfying

(13)

Such a usage level is stable, because if, then and thus individuals are better off not using ITNs, and the average population usage level will thus go down (provided the individuals acts rationally). On the other hand, if, then and thus individuals are better off if they use the ITN and the population usage will thus go up. Here we assume that while individuals cannot accurately assess the overall state of the population (in particular the prevalence of malaria) instantaneously, they can change their behavior at a faster rate than the state of the population changes, in particular when the disease prevalence is either very high or very low. This seems reasonable, since individuals have a complete control over whether they use an ITN and can adapt quickly (though how they act will depend upon the information that they have available, which we consider in the Discussion).

Following [14] , we will evaluate

(14)

where is the probability of the focal individual getting infected in a population with average ITN usage and is the relative cost of the ITN and the cost of getting infected by malaria.

To evaluate, we will use and adapt the model developed in [10] . The probability of a host getting infected is then given by the ratio of the rate of getting infected to the rate of leaving the susceptible state for any reason. Thus,

(15)

3. Analysis

Given a relatively small value of and a relatively large value of, we get from (15) and (5)

(16)

(17)

There will of course be values of just above 0 which are not small compared to, but for the parameters in our model (see Table 1) this happens for a very narrow range of values of, and so the above is a good approximation.

It follows from (14) that

(18)

(19)

and thus, by (16), (17),

(20)

Because by (16), for most such that, we get that

(21)

and otherwise there is a unique satisfying the equilibrium condition (13). The condition is however not realistic for real populations, and thus in practice we will always get a unique. The plots of are shown in Figure 2.

Moreover, the unique is given exactly as a solution of

(22)

where and are given by (7)-(9). As in [10] , (22) happens for a critical value given by

(23)

whenever the term under is nonnegative. The critical ITN usage is then given as a unique solution of a fixed point problem where

(24)

where. The plots of for different parameter values are shown at Figure 3.

4. Results

It follows from our analysis that it is in the individual’s best interest to use the ITN as long as there is malaria present in the population. For the parameter values used above, namely, the optimal usage (from the individual’s perspective) coincide with the average usage in the population that eradicates the disease.

However, the model used shows particular sensitivity to the parameter value. This is unfortunate because the effectiveness of the insecticide sprayed on the ITN deteriorates over 3 - 5 years [2] , the net cannot effectively provide protection for the whole 24 hours, and the mosquitoes may adapt their biting behavior in areas of high ITN coverage [33] . Consequently, the realistic value of is positive and can be relatively close to. As shown in Figure 4 when (or even for larger values of), the malaria does not get eradicated. Still, the force of infection, , decreases with; and the decrease is significant. The quantity is also always positive (close to 1), thus it is in the individual’s interest to keep using the ITN. Consequently, the ITN usage does not eradicate the disease, but helps to significantly reduce its force.

However, in all of the above, we considered that malaria was transmitted between vectors and host during every bite. If we relax this assumption and consider, then again malaria can be eradicated even for larger values of as in Figure 4(c) and Figure 4(d).

5. Discussion

In this paper we have considered a game-theoretical model of ITN usage, allowing individuals in the population to decide whether (and how often) they use ITNs. We have shown that optimal behavior from the individual’s perspective leads to the decrease (or even eradication) of the disease, i.e. an optimal outcome from the popu- lation perspective. In particular if it is not possible to eradicate the disease through ITN usage, individuals use ITNs all the time, which leads to the minimum possible level of malaria. If eradication is possible, individuals select a strategy which is approximately at the level that leads to eradication. Moreover, the optimal behavior does not depend on the exact cost of the ITN use (as long as the cost is smaller than the cost of the disease). This type of outcome is not always the case; see for example [14] .

We have seen that individual strategies lead to the eradication level effectively independently of the cost in our case, because individuals have a very high likelihood of getting infected by the disease whenever the disease is present in the population, due to the high rate of infection (), which is much higher than the rate of natural death, meaning that people become infected with probability almost equal to 1.

We have assumed that individuals are able to adjust their ITN usage strategy faster than changes in the underlying state of the population, such as the prevalence of the disease, to always obtain the optimal level of

usage. It is clear that they are physically able to do this, because to put up or remove an ITN takes a relatively short time. However, they clearly need sufficient information about the state of the population to make a rational decision to change. What information would they have on which to base their decision? It is clear from Figure 2 that except for within a very narrow range the disease is either absent or effectively everyone has it; this information is obvious, and so any individual with the wrong strategy would quickly change it. Thus the popu- lation usage would quickly evolve to a level close to the critical level that we have assumed.

We note that because of the high infection rate, a level of ITN usage close to the eradication level but still below it could formally still lead to high levels of disease prevalence. Thus if individuals had perfect infor- mation about the state of the population they could choose their strategies to achieve the precise level of the equilibrium strategy, which would lead to some intermediate level of infection between 0 and 1. It is our assumption in this paper that they cannot do this precisely. In any case natural variations within the real popu- lation parameters, would mean that the exact value of this critical level would be subject to some fluctuation. The consequence is that the chosen strategy is sufficiently close to the eradication level, that there is a good chance of such eradication occurring, on the assumption that individuals play a fixed bed-net usage strategy.

In reality, it may be that the level of malaria will not have enough time to tend to 0 before individuals in the population notice the low level and give up the use of ITNs. Thus if the malaria level is significantly different to the equilibrium level from our analysis, individual behaviour will prevent it from being eliminated. Thus a more complex dynamically coupled model of the evolution of ITN usage and malaria level may be needed to decide the precise behaviour at such intermediate levels of infection.

Acknowledgements

The research was supported by the Simons Foundation grant #245400 (Jan Rychtář).

Cite this paper

Mark Broom,Jan Rychtář,Tracy Spears-Gill, (2016) The Game-Theoretical Model of Using Insecticide-Treated Bed-Nets to Fight Malaria. Applied Mathematics,07,852-860. doi: 10.4236/am.2016.79076

References