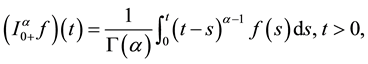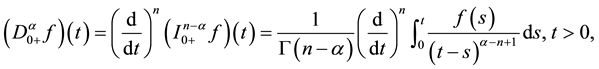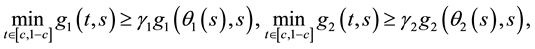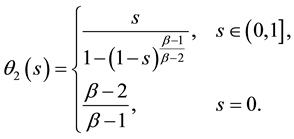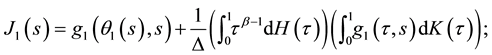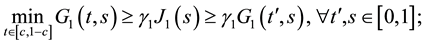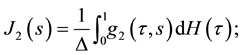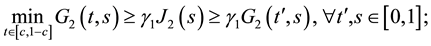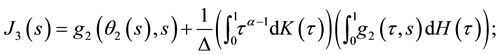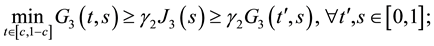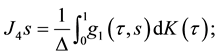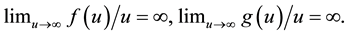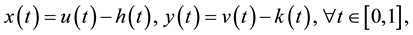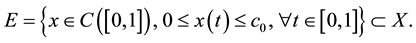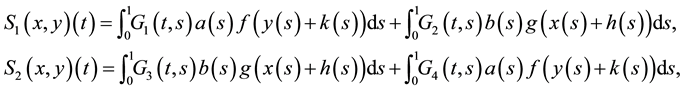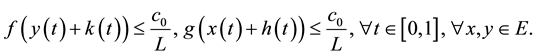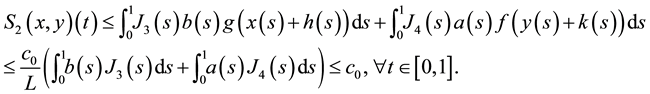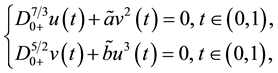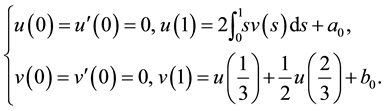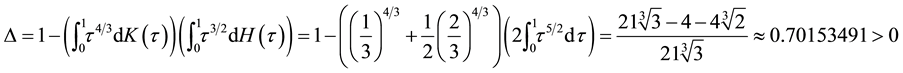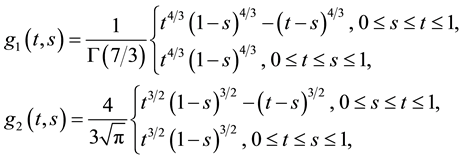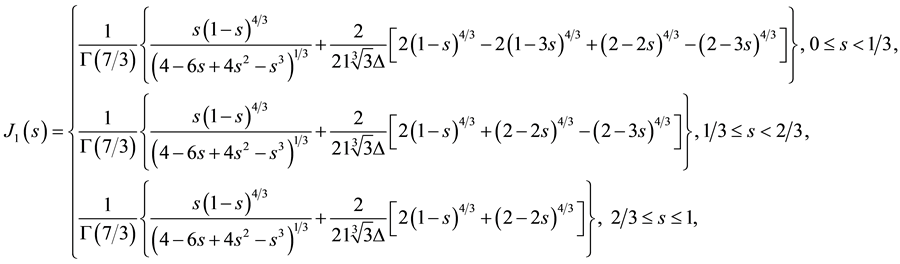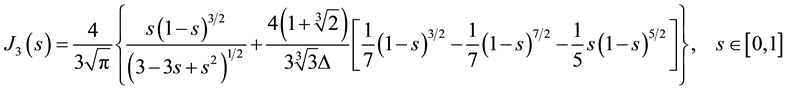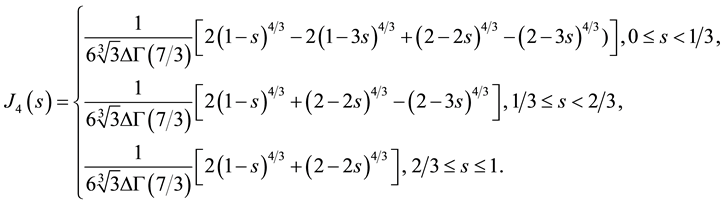Open Journal of Applied Sciences
Vol.05 No.10(2015), Article ID:60616,8 pages
10.4236/ojapps.2015.510059
Positive Solutions for Systems of Coupled Fractional Boundary Value Problems
Johnny Henderson1, Rodica Luca2, Alexandru Tudorache3
1Department of Mathematics, Baylor University, Waco, Texas, USA
2Department of Mathematics, Gh. Asachi Technical University, Iasi, Romania
3Faculty of Computer Engineering and Automatic Control, Gh. Asachi Technical University, Iasi, Romania
Email: Johnny_Henderson@baylor.edu, rluca@math.tuiasi.ro, alexandru.tudorache93@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 September 2015; accepted 24 October 2015; published 27 October 2015
ABSTRACT
We investigate the existence and nonexistence of positive solutions for a system of nonlinear Riemann-Liouville fractional differential equations with coupled integral boundary conditions which contain some positive constants.
Keywords:
Riemann-Liouville Fractional Differential Equations, Coupled Integral Boundary Conditions, Positive Solutions

1. Introduction
Fractional differential equations describe many phenomena in various fields of engineering and scientific dis- ciplines such as physics, biophysics, chemistry, biology (such as blood flow phenomena), economics, control theory, signal and image processing, aerodynamics, viscoelasticity, electromagnetics, and so on (see [1] -[6] ). For some recent developments on the topic, which can be seen in [7] - [19] and the references therein.
In this paper, we consider the system of nonlinear ordinary fractional differential equations
(S) 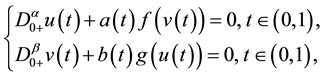
with the coupled integral boundary conditions
(BC) 
where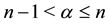 ,
, 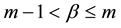 ,
, 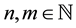 ,
, 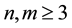 ,
,  and
and 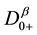 denote the Riemann-Liouville derivatives of orders
denote the Riemann-Liouville derivatives of orders 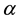 and
and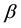 , respectively, the integrals from (BC) are Riemann-Stieltjes integrals,
, respectively, the integrals from (BC) are Riemann-Stieltjes integrals, 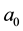 and
and 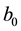 are positive constants.
are positive constants.
Under some assumptions on the functions f and g, we shall prove the existence of positive solutions of problem (S)-(BC). By a positive solution of (S)-(BC), we mean a pair of functions 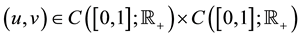 satisfying (S) and (BC) with
satisfying (S) and (BC) with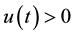 ,
, 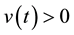 for all
for all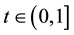 . We shall also give sufficient conditions for
. We shall also give sufficient conditions for
the nonexistence of positive solutions for this problem. Some systems of fractional equations with parameters subject to coupled integral boundary conditions were studied in [20] by using the Guo-Krasnosel’skii fixed point theorem. We also mentioned the paper [21] , where we investigated the existence and multiplicity of positive
solutions for the system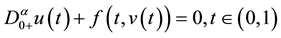
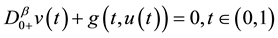
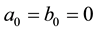
Guo-Krasnosel’skii fixed point theorem. In [21] , the nonlinearities f and g may be nonsingular or singular in 
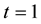
In Section 2, we present some auxiliary results which investigate a system of Riemann-Liouville fractional equations subject to coupled integral boundary conditions. In Section 3, we prove our main results, and an example which supports the obtained results is finally presented in Section 4. In the proof of our existence result, we shall use the Schauder fixed point theorem which we present now.
Theorem 1. Let X be a Banach space and 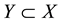
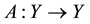
2. Auxiliary Results
We present here the definitions of the fractional integral and Riemann-Liouville fractional derivative of a function, and some auxiliary results from [20] and [22] that will be used to prove our main theorems.
Definition 2.1: The (left-sided) fractional integral of order 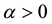
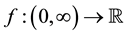
provided the right-hand side is pointwise defined on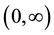
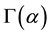
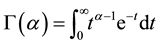
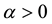
Definition 2.2: The Riemann-Liouville fractional derivative of order 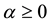
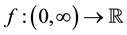
where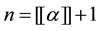
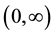
The notation 
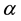
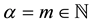
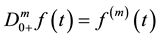
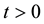
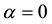
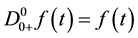
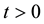
We consider now the fractional differential system
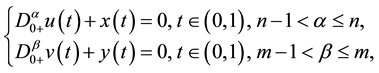
with the coupled integral boundary conditions
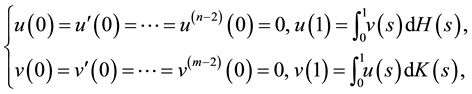
where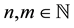
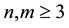
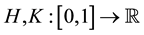
Lemma 1. ( [20] ) If 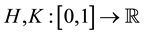
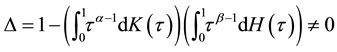
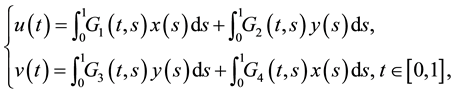
where
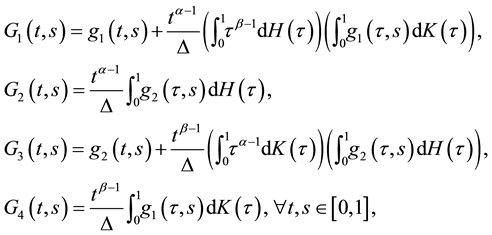
and

Lemma 2. ( [22] ) The functions 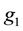
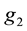
a) 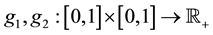
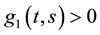
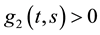
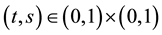
b)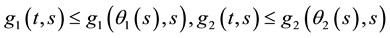

c) For any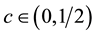
for all
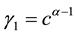

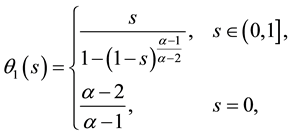
Lemma 3. ( [20] ) If 
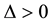

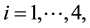
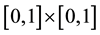
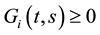

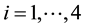
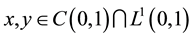
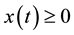
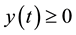
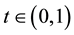
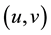
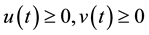
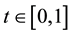
Lemma 4. ( [20] ) Assume that 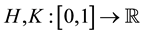

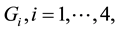
a1)
a2) For every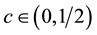
b1)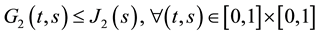
b2) For every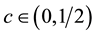
c1)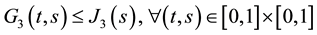
c2) For every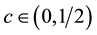
d1)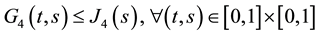
d2) For every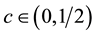
Lemma 5. ( [20] ) Assume that 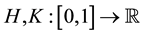
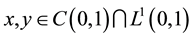

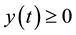
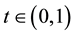
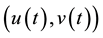
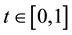
3. Main Results
We present first the assumptions that we shall use in the sequel.
(J1) 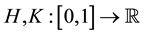
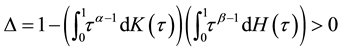
(J2) The functions 
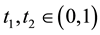
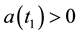
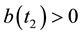
(J3) 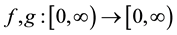


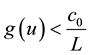
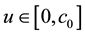
where 
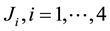
(J4) are continuous functions and satisfy the conditions
By assumption (J2) we deduce that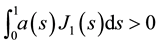
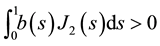

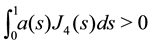
Our first theorem is the following existence result for problem (S)-(BC).
Theorem 2. Assume that assumptions (J1)-(J3) hold. Then problem (S)-(BC) has at least one positive solution for 
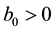
Proof. We consider the system of ordinary fractional differential equations
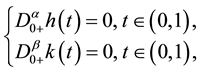
with the coupled integral boundary conditions
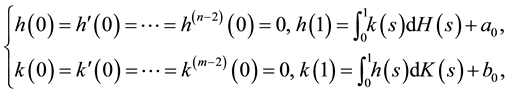
with 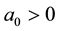
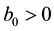
The above problem (6)-(7) has the solution
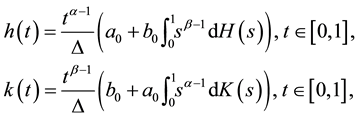
where 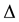
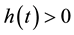
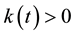
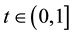
We define the functions 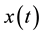
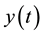
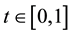
where 
with the boundary conditions
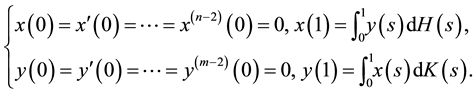
Using the Green’s functions

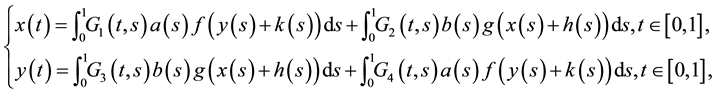
where 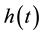
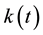
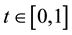
We consider the Banach space 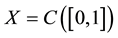



We also define the operators 
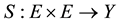
for all
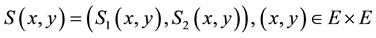
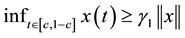
For sufficiently small 
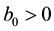
Then, by using Lemma 3, we obtain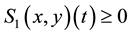

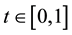

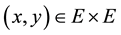
and
Therefore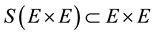
Using standard arguments, we deduce that S is completely continuous. By Theorem 1, we conclude that S has a fixed point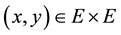
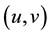

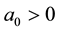
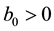
In what follows, we present sufficient conditions for the nonexistence of positive solutions of (S)-(BC).
Theorem 3. Assume that assumptions (J1), (J2) and (J4) hold. Then problem (S)-(BC) has no positive solution for 
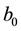
Proof. We suppose that 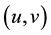
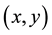
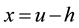
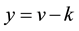
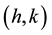
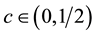
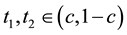
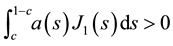
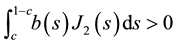
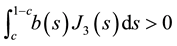
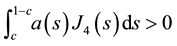
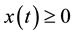

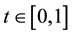
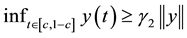
Using now (8), we deduce that 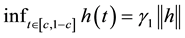
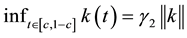
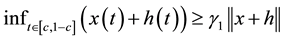
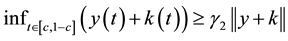
We now consider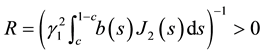
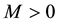
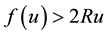
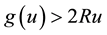

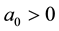

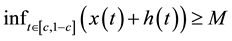
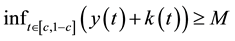
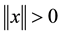
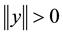
Now by using Lemma 4 and the above considerations, we have
Therefore, we obtain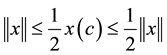
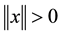
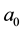
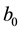
4. An Example
We consider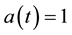
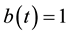
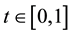
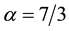
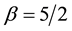
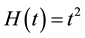
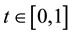
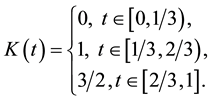
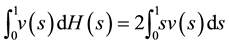
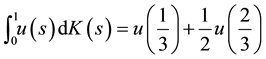
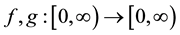
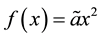
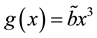
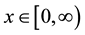

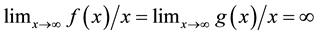
Therefore, we consider the system of fractional differential equations
(S0)
with the boundary conditions
(BC0)
Then we obtain
We also deduce
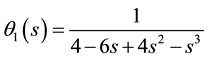
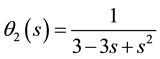


Then we deduce that assumptions (J1), (J2) and (J4) are satisfied. In addition, by using the above functions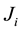

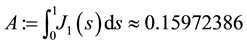
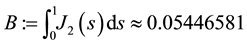

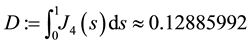
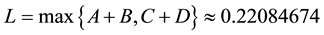
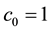
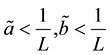
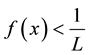
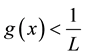
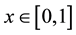
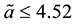
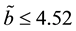
assumption (J3) is also satisfied. By Theorems 2 and 3 we deduce that problem (S0)-(BC0) has at least one positive solution for sufficiently small 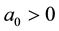
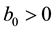
Acknowledgements
The work of R. Luca and A. Tudorache was supported by a grant of the Romanian National Authority for Scientific Research, CNCS-UEFISCDI, project number PN-II-ID-PCE-2011-3-0557.
Cite this paper
JohnnyHenderson,RodicaLuca,AlexandruTudorache, (2015) Positive Solutions for Systems of Coupled Fractional Boundary Value Problems. Open Journal of Applied Sciences,05,600-608. doi: 10.4236/ojapps.2015.510059
References
- 1. Baleanu, D., Diethelm, K., Scalas, E. and Trujillo, J.J. (2012) Fractional Calculus Models and Numerical Methods. Series on Complexity, Nonlinearity and Chaos. World Scientific, Boston.
- 2. Das, S. (2008) Functional Fractional Calculus for System Identification and Control. Springer, New York.
- 3. Kilbas, A.A., Srivastava, H.M. and Trujillo, J.J. (2006) Theory and Applications of Fractional Differential Equations. North-Holland Mathematics Studies, Elsevier Science, Amsterdam.
- 4. Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
- 5. Sabatier, J., Agrawal, O.P. and Machado, J.A.T., Eds. (2007) Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering. Springer, Dordrecht.
- 6. Samko, S.G., Kilbas, A.A. and Marichev, O.I. (1993) Fractional Integrals and Derivatives. Theory and Applications. Gordon and Breach, Yverdon.
- 7. Agarwal, R.P., Andrade, B. and Cuevas, C. (2010) Weighted Pseudo-Almost Periodic Solutions of a Class of Semilinear Fractional Differential Equations. Nonlinear Analysis, Real World Applications, 11, 3532-3554. http://dx.doi.org/10.1016/j.nonrwa.2010.01.002
- 8. Agarwal, R.P., Zhou, Y. and He, Y. (2010) Existence of Fractional Neutral Functional Differential Equations. Computers and Mathematics with Applications, 59, 1095-1100. http://dx.doi.org/10.1016/j.camwa.2009.05.010
- 9. Aghajani, A., Jalilian, Y. and Trujillo, J.J. (2012) On the Existence of Solutions of Fractional Integro-Differential Equations. Fractional Calculus and Applied Analysis, 15, 44-69. http://dx.doi.org/10.2478/s13540-012-0005-4
- 10. Ahmad, B. and Ntouyas, S.K. (2012) Nonlinear Fractional Differential Equations and Inclusions of Arbitrary Order and Multi-Strip Boundary Conditions. Electronic Journal of Differential Equations, 2012, 1-22. http://dx.doi.org/10.14232/ejqtde.2012.1.93
- 11. Ahmad, B. and Ntouyas, S.K. (2012) A Note on Fractional Differential Equations with Fractional Separated Boundary Conditions. Abstract and Applied Analysis, 2012, Article ID: 818703.
- 12. Bai, Z. (2010) On Positive Solutions of a Nonlocal Fractional Boundary Value Problem. Nonlinear Analysis, 72, 916-924. http://dx.doi.org/10.1016/j.na.2009.07.033
- 13. Balachandran, K. and Trujillo, J.J. (2010) The Nonlocal Cauchy Problem for Nonlinear Fractional Integrodifferential Equations in Banach Spaces. Nonlinear Analysis, 72, 4587-4593. http://dx.doi.org/10.1016/j.na.2010.02.035
- 14. El-Shahed, M. and Nieto, J.J. (2010) Nontrivial Solutions for a Nonlinear Multi-Point Boundary Value Problem of Fractional Order. Computers and Mathematics with Applications, 59, 3438-3443. http://dx.doi.org/10.1016/j.camwa.2010.03.031
- 15. Graef, J.R., Kong, L., Kong, Q. and Wang, M. (2012) Uniqueness of Positive Solutions of Fractional Boundary Value Problems with Non-Homogeneous Integral Boundary Conditions. Fractional Calculus and Applied Analysis, 15, 509- 528. http://dx.doi.org/10.2478/s13540-012-0036-x
- 16. Jiang, D. and Yuan, C. (2010) The Positive Properties of the Green Function for Dirichlet-Type Boundary Value Problems of Nonlinear Fractional Differential Equations and Its Application. Nonlinear Analysis, 72, 710-719. http://dx.doi.org/10.1016/j.na.2009.07.012
- 17. Liang, S. and Zhang, J. (2009) Positive Solutions for Boundary Value Problems of Nonlinear Fractional Differential Equation. Nonlinear Analysis, 71, 5545-5550. http://dx.doi.org/10.1016/j.na.2009.04.045
- 18. Yuan, C. (2010) Multiple Positive Solutions for -Type Semipositone Conjugate Boundary Value Problems of Nonlinear Fractional Differential Equations. Electronic Journal of Qualitative Theory of Differential Equations, 2010, 1-12. http://dx.doi.org/10.14232/ejqtde.2010.1.36
- 19. Yuan, C., Jiang, D., O’Regan, D. and Agarwal, R.P. (2012) Multiple Positive Solutions to Systems of Nonlinear Semipositone Fractional Differential Equations with Coupled Boundary Conditions. Electronic Journal of Qualitative Theory of Differential Equations, 2012, 1-17. http://dx.doi.org/10.14232/ejqtde.2012.1.13
- 20. Henderson, J. and Luca, R. (2014) Positive Solutions for a System of Fractional Differential Equations with Coupled integral Boundary Conditions. Applied Mathematics and Computation, 249, 182-197. http://dx.doi.org/10.1016/j.amc.2014.10.028
- 21. Henderson, J., Luca, R. and Tudorache, A. (2015) On a System of Fractional Differential Equations with Coupled integral Boundary Conditions. Fractional Calculus and Applied Analysis, 18, 361-386. http://dx.doi.org/10.1515/fca-2015-0024
- 22. Henderson, J. and Luca, R. (2013) Positive Solutions for a System of Nonlocal Fractional Boundary Value Problems. Fractional Calculus and Applied Analysis, 16, 985-1008. http://dx.doi.org/10.2478/s13540-013-0061-4
- 23. Henderson, J. and Luca, R. (2014) Existence and Multiplicity of Positive Solutions for a System of Fractional Boundary Value Problems. Boundary Value Problems, 2014, 60. http://dx.doi.org/10.1186/1687-2770-2014-60
- 24. Henderson, J., Luca, R. and Tudorache, A. (2015) Positive Solutions for a Fractional Boundary Value Problem. Nonlinear Studies, 22, 1-13.
- 25. Luca, R. and Tudorache, A. (2014) Positive Solutions to a System of Semipositone Fractional Boundary Value Problems. Advances in Difference Equations, 2014, 179. http://dx.doi.org/10.1186/1687-1847-2014-179
- 26. Henderson, J. and Luca, R. (2015) Boundary Value Problems for Systems of Differential, Difference and Fractional Equations: Positive Solutions. Elsevier, Amsterdam.