Engineering
Vol. 3 No. 7 (2011) , Article ID: 6146 , 9 pages DOI:10.4236/eng.2011.37082
A Prediction Method for in-Plane Permeability and Manufacturing Applications in the VARTM Process
1Engineering Science and Ocean Engineering, National Taiwan University, Chinese Taipei
2R & D Department, United Ship Design & Development Center, Chinese Taipei
3Business and Entrepreneurial Management, Kai Nan University, Taoyuan, Chinese Taipei
E-mail: *yjlee@ntu.edu.tw
Received April 15, 2011; revised May 3, 2011; accepted May 20, 2011
Keywords: Prediction Method, in-Plane Permeability, Manufacturing Simulation, Infusion Scenarios
ABSTRACT
VARTM (Vacuum Assisted Resin Transfer Molding) is a popular method for manufacturing large-scaled, single-sided mold composite structures, such as wind turbine blades and yachts. Simulation to find the proper infusion scenario before manufacturing is essential to avoid dry spots as well as incomplete saturation and various fiber weaves with different permeability affect numerical simulation tremendously. This study focused on deriving the in-plane permeability prediction method for FRP (Fiber Reinforced Plastics) laminates in the VARTM process by experimental measurements and numerical analysis. The method provided an efficient way to determine the permeability of laminates without conducting lots of experiments in the future. In-plane permeability imported into the software, RTM-Worx, to simulate resin flowing pattern before the infusion experiments of a 3D ship hull with two different infusion scenarios. The close agreement between experiments and simulations proved the correctness and applicability of the prediction method for the in-plane permeability.
1. Introduction
VARTM (Vacuum Assisted Rein Transfer Molding) has been employed successfully to manufacture FRP (Fiber Reinforced Plastics) ship hull structures since 1994 [1] and other large structures, such as wind turbine blades and yachts [2-3]. In this manufacturing technique, the fiber lay-up is placed in advance above a one-sided mold, and resin injects into the fiber lay-up under one pressure gradient as vacuum is applied. This procedure provides the advantages of low VOC (Volatile Organic Compounds) emission as well as stable and excellent mechanical properties of products. The manufacturing failure risks, such as void contain and incomplete saturation, increase as the structure dimension increases. Accordingly, resin flowing prediction before manufacturing complex structures with various fiber laminates is essential. The CV-FEM (control volume finite element method) is utilized to explicate the behavior of resin flowing in fiber laminates [4,5]. With respect to the VARTM simulation, Mohan [6] modeled flow in channels based on a finite element method. Sun [7] and Ni [8] applied CV-FEM to predict the filling time and pattern associated with high-permeable medium and grooves in the SCRIMP process. Koorevaar [9,10] adopted 2.5D flow models, meaning that resin flow in the thickness direction is neglected, although the geometries are described as 3D, to simulate the VARTM and RTM process. The VARTM simulation involves with parameters, such as the viscosity of resin, the porosity and permeability of fiber laminates. The permeability of FRP laminates is critical in the manufacturing process and numerous researchers have investigated the measurements and analytical models of permeability [7,8] [11-15]. Sun [7] and Ni [8] set up a device to visualize the experimental results and measurements of permeability. Wang and Demaria [11-13] characterized the in-plane permeability of woven fabrics and proposed a predictive model. Wu [14] and Nedanov [15] researched the trans-plane permeability by theory and experiments to describe 3D permeability of fiber laminates. Some researchers have described the flow using equivalent permeability [16-18]. For example, Dong [18] increased the thickness of the distribution medium and/or the fiber preform to obtain equivalent material permeability. Besides, the Kozeny-Carman equation was commonly utilized to discuss the flow impregnates inside the porous material when considering the dimension of fiber [19-22]. Gebart [19] investigated the permeability of an idealized unidirectional reinforcement through the Darcy’s law and Kozeny-Carman equation, and Rahatekar [21] used the permeability models through Kozeny-Carman equation to discuss the relationship between injection pultrusion pressure and process control parameters.
The infusion scenario in the VARTM process including the numbers of flowing channels, injection and venting ports, and the triggering timing of the injection gates etc. determines the impregnation of FRP products. Precise evaluation of the resin flowing pattern before fabrication reduces the risk and cost of manufacturing failure. Therefore, some researchers [23,24] focused on how to arrange and improve the infusion process to avoid dry spots and incompletely saturation. Han [25] and Kang [26] analyzed the VARTM process under different vacuum conditions as well as infusion strategy and simulated the infusion process of a boat hull. The abovementioned studies have provided feasible methods for measuring permeability, but permeability measurement through the experiments is a time-consuming procedure. Hence, the development of simplified macroscopic models for predicting permeability of FRP laminates composing of various woven fabrics is beneficial for simulating and discussing the manufactures of complex structures with various infusion scenarios in the VARTM process. This study investigated the in-plane permeability for single and multi types of fiber laminates by the permeability experiments. A prediction method for the in-plane permeability was established by defining the parameter of “thickness porosity”, and the method provided an efficient way to determine the in-plane permeability of FRP laminates without conducting time-consuming experiments. Flowing patterns of a 3D ship hull with two different infusion scenarios were simulated to compare with the manufacturing experiments. The close agreement between experiments and simulations proved the correctness and applicability of the prediction method for the in-plane permeability.
2. In-Plane Permeability Experiments
Experimental Measurements and Discussion
Several scholars have utilized Equation (1), derived from Darcy’s Law, to describe the resin flowing process inside the porous space of fabrics under the RTM or VARTM method from 1980 to date.
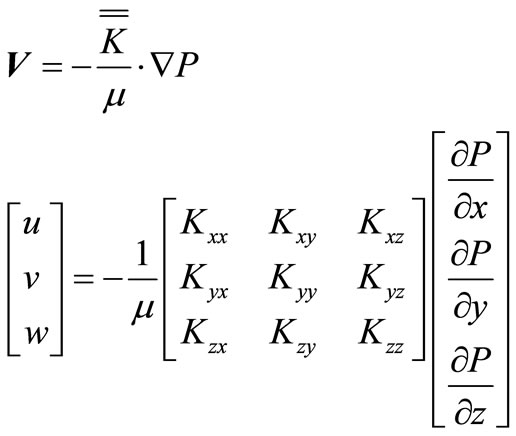 (1)
(1)
where V represents the Darcian Velocity,  is the tensor of permeability, μ is the viscosity of resin, and
is the tensor of permeability, μ is the viscosity of resin, and  is the gradient of pressure. In the research, realizing the in-plane permeant characteristic of FRP laminates was the main objective, and the length and width scale of fiber laminates was relatively larger than its thickness. Hence, the governing Equation (1) transformed into a 1D flowing Equation (2) when operating the rectangle experimental arrangement.
is the gradient of pressure. In the research, realizing the in-plane permeant characteristic of FRP laminates was the main objective, and the length and width scale of fiber laminates was relatively larger than its thickness. Hence, the governing Equation (1) transformed into a 1D flowing Equation (2) when operating the rectangle experimental arrangement.
 (2)
(2)
where 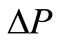 is the pressure gradient,
is the pressure gradient,  is the porosity of laminate, L is the flow front, and t is the infusion time. Equation (2) reveals that the combination of value L2/t, evaluating from the video records of flowing processes, the porosity of fiber laminates, and resin viscosity derives the in-plane permeability (K).
is the porosity of laminate, L is the flow front, and t is the infusion time. Equation (2) reveals that the combination of value L2/t, evaluating from the video records of flowing processes, the porosity of fiber laminates, and resin viscosity derives the in-plane permeability (K).
The viscosity of polyester resin, μ, changing with temperature (Figure 1(a)) was measured by the Brookfield viscometer and the thermostat sink (Figure 1(b)). The infusion time of the experimental process did not exceed 30 minutes and the ambient temperature did not change sharply during the infusion time. Accordingly, the viscosity was reasonably regarded as constant throughout the whole process. Figure 2(a) displays the in-plane permeability experimental schema. The fiber assembly was rectangular, and the dimensions of fiber laminates were 48 cm × 16 cm. Pressure gradient designed to be along the length of fiber laminates, from injection gate to venting port. The extensible spring linking with the injection gate was placed in the starting position to transform a point-injection into a line-injection, and consequently resin flowing front was perpendicular to the infusion direction (Figure 2(b)). Table 1 presents the single-type fiber laminates under consideration, including strand chopped mat, woven roving and axial fabrics with different area density and numbers of layers. Figure 3 shows the relationship between flowing fronts and its consuming infusion time which determines the permeability of FRP laminates. Initial time-delay region on the bottom surface was neglected due to the transverse-plane infusion from top surface to bottom
 (a) (b)
(a) (b)
Figure 1. Viscosity measurement of polyester resin.
 (a) (b)
(a) (b)
Figure 2. In-plane permeability experiment.

Table 1. Single-type experimental laminates.
surface. Figure 4 shows the experimental permeability results of single-type laminates, and the horizontal axis represented the experimental laminates and the vertical axis was the in-plane permeability. The right-most bar symbolizing of D + P was the assembly consisted only with distribution medium and peel ply, and tested its permeability by considering the nestling effect [7], which was about the effect of fiber layers inserting mutually. Resin flowed more rapidly than other laminates because no fiber ply needed to be impregnated during the infusion process and the permeability, 1.88 × 10–9 m2, was the highest between these results. The black and gray bars respectively represented the permeability values on the top and bottom surfaces. Measured permeability on the top surfaces was larger than that of the bottom surfaces because the distribution medium arranged on the top surface of fiber laminates and experimental permeability decreased as the same types of fiber layers increased (Figure 4(a)). Figure 4(b) shows experimental results of 7 fibrous layers in one assembly and the permeability decreased as the area-density of various fibrous weaves increased.
3. Permeability Prediction and Verification
3.1. Permeability Prediction of Fiber Laminates with Single-Type Weave
The aforementioned steps derive the permeability of fiber laminates but the approach is time-consuming and
 (a) (b)
(a) (b)
Figure 3. Flowing process of (a) M450 × 7 and (b) DBLT1900 × 7.
 (a) (b)
(a) (b)
Figure 4. In-plane permeability of (a) Mat-300 and (b) various fibrous weaves.
inefficient. Therefore, this research established a predictive method to derive the permeability of fiber laminates with no more operation of permeability experiments. Observing the experimental results revealed the in-plane permeability dropped as the increase of layer numbers and/or area-density of fiber weaves and changing these parameters meant changing the porous space inside FRP laminates. The length and width of each experimental specimen was the same, and hence thickness porosity, Sf, was defined as Equation (3) to display the change of porous space in the thickness direction.
 (3)
(3)
where tf and  are the thickness and the porosity of fiber laminate respectively. The parameter, Sf, provided a macroscopic viewpoint to discuss the resin flowing behavior and therefore the fiber diameter of weave was not considered herein to discuss permeability and flowing process [19].
are the thickness and the porosity of fiber laminate respectively. The parameter, Sf, provided a macroscopic viewpoint to discuss the resin flowing behavior and therefore the fiber diameter of weave was not considered herein to discuss permeability and flowing process [19].
The experimental data of top surface were rearranged in terms of thickness porosity, Sf (horizontal axis) and permeability, K (vertical axis) as Figure 5 showed and the dots were experimental results including top and bottom surfaces. The data significantly exhibited a decreasing trend because larger thickness porosity, Sf, meant more porosity space inside fiber laminates that resin should infuse into. Hence two regressive curves were made to describe the relationship between thickness porosity and permeability on top and bottom surface. Equations (4) and (5) showed permeability tended to zero, as the flowing front stagnated, when the thickness porosity was extremely large, as limitless infusion space inside fiber laminates, and it conformed to the physical concept.

Figure 5. Experimental permeability of single-type fiber laminates.
Top surface: (4)
(4)
Bottom surface: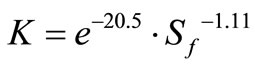 (5)
(5)
3.2. Predictive Permeability Verification by Fiber Laminates with Multi-Type Weave
Figure 5 showed the permeability predictive curves of fiber laminates with single-type weave. However, the laminates applying in manufacturing large structures, such as yachts and wind turbine blades, are multi-type weave which includes chopped strand mats and different types of fiber weaves. Table 2 displays the experimental laminates of multi-type weave as well as the measurements of thickness and porosity. The experimental permeability of each specimen derived from the in-plane flowing experiments and the predictive permeability obtained from the fitting curves showed in Table 3. The diversity of predictive and experimental permeability in Table 3 almost below ±15% and the experiments with large diversity happened in thick laminates, such as (MD) × 4 + M and (MLT) × 5 + M, because the channel effect [8] easily occurred in the sides of thick laminates and affected the observation of flowing process. The permeability of single-type laminates with white dots and data of multi-type laminates with black dots on top and bottom surfaces displays in Figure 6(a) and (b) respectively. The permeability of multi-type laminates (black dots) superimposed on the data distribution of single-type laminates (white dots) and it meant the parameter of thickness porosity, Sf, was also suitable to predict the permeability of fiber laminates with multitype weave. The fitting curves were recalculated to get the new predictive equations as Equation (6), Equation (7), and Figure 6 shows. Therefore the permeability of various fiber lay-up or sequences could be derived through the predictive equations without executing the time-consuming inplane permeability experiments, and the permeability was significant as running the simulation of infusion process.
Top surface: (6)
(6)
Bottom surface: (7)
(7)
4. Simulations and Experiments on Ship Hulls
4.1. Flowing Process Simulation with Various Infusion Scenarios
The predictive method for the in-plane permeability of fiber laminates was established and then was applied to manufacture a FRP ship hull. The target ship was designed for the Coast Guard Administration of Taiwan, and was measured 4.25 meters long and 1.66 meters wide. The designed laminate over the entire hull was (Mat-300 + DBLT-1900) × 2 + Mat-300 and its permeability was obtained from the predictive equations by only measuring the thickness and porosity of the designed laminate to input into the simulation software, RTM-Worx, to simulate the manufacturing process. Two injection strategies, the parallel scenario (Figure 7(a)) and the fish-bone scenario (Figure 7(b)), were used to analyze the simulated flowing pattern. The parallel strategy showed three parallel injection lines arranged in the longitudinal direction of the ship and the venting ports located around the hull side. The central injection gate above the keel was opened first, and the other two injection gates were triggered later as the flowing front passed through them about 30 cm. The fish-bone scenario showed one principal injection line along the keel, six minor injection lines perpendicular to the main line, and three injection gates on the principal injection line. Several simulations were executed to find the proper infusion arrangement including length of infusion lines, numbers and position of injection gates etc. for the target ship. Simulation before manufacturing is important and able to check whether the infusion time is less than the glue time and to ensure dry spots do not occur during the whole infusion process.
The simulated profile with the parallel strategy, Figure 8(a), showed a smooth front flowed in the whole infusion process and was beneficial to avoid dry spots as well as unsaturated impregnation. However, monitoring

Table 2. Experimental laminates of multi-type weave.

Table 3. Predictive and experimental permeability on multi-type laminates.
 (a) (b)
(a) (b)
Figure 6. Permeability predictive curves on (a) top surface and (b) bottom surface.
 (a) (b)
(a) (b)
Figure 7. (a) Parallel and (b) fish-bone infusion scenario.
the flowing condition to decide the trigger time of each injection gate was a disadvantage of the parallel strategy, especially in manufacturing large components. The fishbone infusion showed a sawtooth contour in the initial stage (Figure 9(a)) and finally had a smooth flowing front into the venting line. All injection gates triggered at the beginning of infusion was an efficient scenario without operating each injection gate separately. Exact simulation of the fish-bone scenario before manufacturing was an important work to avoid infusion failures.
4.2. Infusion Measurements and Comparison with Simulations
Two manufacturing measurements of the ship hull with the parallel and fish-bone scenario were completed to compare with the simulated results. Figures 8 and 9 showed the comparison contour between simulation and experiment with two different infusion strategies.
 (a) (b)
(a) (b)
Figure 8. Simulation and experiment of parallel infusion scenario.
Both strategies displayed similar flowing shapes during the whole process. Total infusion time of two scenarios showed in Table 4 and both experimental infusions were longer than the simulation time because of fiber overlap (Figure 10) near the keel to ensure structural safety. The small diversity explained the predictive method for the in-plane permeability of fiber laminates was validated and able to simulate the VARTM infusion process.
5. Conclusions
The permeability, K, reflecting the flowing ability of
 (a) (b)
(a) (b)
Figure 9. Simulation and experiment of fish-bone infusion scenario.

Figure 10. Overlap on the keel region.

Table 4. Experiments and simulations of ship-hull infusions.
fiber laminates depended on the thickness porosity, Sf, in the macroscopic viewpoint. Although the compressibility effect during the flowing process was not discussed, the predictive method derived from experimental data had already included the effect. Consequently, the predictive method by defining the parameter Sf was proposed to derive the in-plane permeability of fiber laminates under the VARTM process. The fine agreement between numerical simulations and experiments of a ship hull explained well applicability of the predictive method as manufacturing FRP products. Two infusion scenarios, parallel and fish-bone, had particular advantages. The experience of operating the software showed the parallel strategy was suitable for a slender and large structure, such as wind turbine blades, while the fish-bone strategy was applicable to manufacture structures without too large aspect ratio, such as a small boat. The predictive method for the in-plane permeability was established in the study and was beneficial to simulate the manufactures of FRP products under the VARTM process.
6. Acknowledgements
The authors would like to thank the National Science Council of the Republic of China, Taiwan for financially supporting this research. (NSC 94-2622-E-002-015-CC3).
7. REFERENCES
- B. Pfund, “Resin Infusion in the US Marine Industry,” Reinforced Plastics, Vol. 38, No. 1, 1994, pp. 32-34. doi:10.1016/0034-3617(94)90021-3
- C. Williams, J. Summerscales and S. Grove, “Resin Infusion under Flexible Tooling (RIFT): A Review,” Composite Part A-Applied Science and Manufacturing, Vol. 27, No. 7, 1996, pp. 517-524. doi:10.1016/1359-835X(96)00008-5
- W. D. Brouwer, E. C. F. C. van Herpt and M. Labordus, “Vacuum Injection Moulding for Large Structural Applications,” Composite Part A-Applied Science and Manufacturing, Vol. 34, No. 6, 2003, pp. 551-558. doi:10.1016/S1359-835X(03)00060-5
- W. B. Young, K. Han, L. H. Fong and L. J. Lee, “Flow Simulation in Molds with Preplaced Fiber Mats,” Polymer Composites, Vol. 12, No. 6, 1991, pp. 391-403. doi:10.1002/pc.750120604
- L. J. Lee, W. B. Young and R. J. Lin, “Mold Filling and Curing Modeling of RTM and SCRIMP Processes,” Composite Structures, Vol. 27, No. 1-2, 1994, pp. 109- 120. doi:10.1016/0263-8223(94)90072-8
- R. V. Mohan, D. R. Shires, K. K. Tamma and N. D. Ngo, “Flow Channels/Fiber Impregnation Studies for the Process Modeling/Analysis of Complex Engineering Structures Manufactured by Resin Transfer Molding,” Polymer Composites, Vol. 19, No. 5, 1998, pp. 527-542. doi:10.1002/pc.10127
- X. Sun, S. Li and L. J. Lee, “Molding Filling Analysis in Vacuum-Assisted Resin Transfer Molding, Part I: Scrimp Based on a High-Permeable Medium,” Polymer Composites, Vol. 19, No. 6, 1998, pp. 807-817. doi:10.1002/pc.10155
- J. Ni, S. J. Li, X. D. Sun and L. J. Lee, “Mold Filling Analysis in Vacuum-Assisted Resin Transfer Molding. Part II: SCRIMP Based on Grooves,” Polymer Composites, Vol. 19, No. 6, 1998, pp. 818-829. doi:10.1002/pc.10156
- A. Koorevaar, “Simulation of Liquid Injection Molding,” Proceedings of 23rd SAMPE Europe Conference, Paris, 9-11 April 2002.
- A. Koorevaar, “Fast, Accurate, Reliable 3D Reactive RTM Simulation,” Proceedings of ISCM 2002 Conference, Flevoland, 30-31 May 2002.
- T. J. Wang, C. H. Wu and L. J. Lee, “In-Plane Permeability Measurement and Analysis in Liquid Composite Molding,” Polymer Composites, Vol. 15, No. 4, 1994, pp. 278-288. doi:10.1002/pc.750150406
- C. Demaria, E. Ruiz and F. Trochu, “In-Plane Anisotropic Permeability Characterization of Deformed Woven Fabrics by Unidirectional Injection. Part I: Experimental Results,” Polymer Composites, Vol. 28, No. 6, 2007, pp. 797-811. doi:10.1002/pc.20107
- C. Demaria, E. Ruiz and F. Trochu, “In-Plane Anisotropic Permeability Characterization of Deformed Woven Fabrics by Unidirectional Injection. Part II: Prediction Model and Numerical Simulations,” Polymer Composites, Vol. 28, No. 6, 2007, pp. 812-827. doi:10.1002/pc.20108
- C. H. Wu, T. J. Wang and L. J. Lee, “Trans-Plane Permeability Measurement and Its Application in Liquid Composite Molding,” Polymer Composites, Vol. 15, No. 4, 1994, pp. 289-298. doi:10.1002/pc.750150407
- P. B. Nedanov and S. G. Advani, “A Method to Determine 3D Permeability of Fibrous Reinforcements,” Journal of Composite Materials, Vol. 36, No. 2, 2002, pp. 241-254. doi:10.1177/0021998302036002462
- V. M. A. Calado and S. G. Advani, “Effective Average Permeability of Multi-Layer Preforms in Resin Transfer Molding,” Composites Science and Technology, Vol. 56, No. 5, 1996, pp. 519-531. doi:10.1016/0266-3538(96)00037-1
- R. Chen, C. Dong, Z. Liang, C. Zhang and B. Wang, “Flow Modeling and Simulation for Vacuum Assisted Resin Transfer Molding Process with the Equivalent Permeability Method,” Polymer Composites, Vol. 25, No. 2, 2004, pp. 146-164. doi:10.1002/pc.20012
- C. Dong, “An Equivalent Medium Method for the Vacuum Assisted Resin Transfer Molding Process Simulation,” Journal of Composite Materials, Vol. 40, No. 13, 2006, pp. 1193-1213. doi:10.1177/0021998305057429
- B. R. Gebart, “Permeability of Unidirectional Reinforcements for RTM,” Journal of Composite Materials, Vol. 26, No. 8, 1992, pp. 1100-1133. doi:10.1177/002199839202600802
- P. Simacek, V. Neacsu and S. G. Advani, “A Phenomenological Model for Fiber Tow Saturation of Dual Scale Fabrics in Liquid Composite Molding,” Polymer Composites, Vol. 31, No. 11, 2010, pp. 1881-1889. doi:10.1002/pc.20982
- S. S. Rahatekar and J. A. Roux, “Numerical Simulation of Pressure Variation and Resin Flow in Injection Pultrusion,” Journal of Composite Materials, Vol. 37, No. 12, 2003, pp. 1067-1082. doi:10.1177/0021998303037012005
- W. D. Carrier Ⅲ, “Goodbye, Hazen; Hello, KozenyCarman,” Journal of Geotechnical and Geoenvironmental Engineering, Vol. 129, No. 11, 2003, pp. 1054-1056. doi:10.1061/(ASCE)1090-0241(2003)129:11(1054)
- K. T. Hsiao, J. W. Gillespie Jr., S. G. Advani and B. K. Fink, “Role of Vacuum Pressure and Port Locations on Flow Front Control for Liquid Composite Molding Process,” Polymer Composites, Vol. 22, No. 5, 2001, pp. 660- 667. doi:10.1002/pc.10568
- A. R. Nalla, M. Fuqua, J. Glancey and B. Lelievre, “A Multi-Segment Injection Line and Real-Time Adaptive, Model-Based Controller for Vacuum Assisted Resin Transfer Molding,” Composite Part A—Applied Science and Manufacturing, Vol. 38, No. 3, 2007, pp.1058-1069. doi:10.1016/j.compositesa.2006.06.021
- K. Han, S. Jiang, C. Zhang and B. Wang, “Flow Modeling and Simulation of SCRIMP for Composites Manufacturing,” Composite Part A—Applied Science and Manufacturing, Vol. 31, No. 1, 2000, pp. 79-86. doi:10.1016/S1359-835X(99)00053-6
- M. K. Kang, W. I. Lee and H. T. Hahn, “Analysis of Vacuum Bag Resin Transfer Molding Process,” Composite Part A—Applied Science and Manufacturing, Vol. 32, No. 11, 2001, pp. 1553-1560. doi:10.1016/S1359-835X(01)00012-4

