Journal of Modern Physics
Vol.08 No.04(2017), Article ID:75084,79 pages
10.4236/jmp.2017.84045
Origin of Magnetic Fields of Stellar Objects in the Universe Based on the 5D Projection Theory
Peter C. W. Fung1*, K. W. Wong2
1Department of Physics, University of Hong Kong, Hong Kong, China
2Department of Physics and Astronomy, University of Kansas, Kansas, USA

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 23, 2017; Accepted: March 28, 2017; Published: March 31, 2017
ABSTRACT
Beginning with a 5D homogeneous universe [1] , we have provided a plausible explanation of the self-rotation phenomenon of stellar objects previously with illustration of large number of star samples [2] , via a 5D-4D projection. The origin of such rotation is the balance of the angular momenta of stars and that of positive and negative charged e-trino pairs, within a  void of the stellar object, the existence of which is based on conservation/parity laws in physics if one starts with homogeneous 5D universe. While the in-phase e-trino pairs are proposed to be responsible for the generation of angular momentum, the anti-phase but oppositely charge pairs necessarily produce currents. In the 5D to 4D projection, one space variable in the 5D manifold was compacted to zero in most other 5D theories (including theories of Kaluza-Klein and Einstein [3] [4] ). We have demonstrated, using the Fermat’s Last Theorem [5] , that for validity of gauge invariance at the 4D-5D boundary, the 4th space variable in the 5D manifold is mapped into two current rings at both magnetic poles as required by Perelman entropy mapping; these loops are the origin of the dipolar magnetic field. One conclusion we draw is that there is no gravitational singularity, and hence no black holes in the universe, a result strongly supported by the recent discovery of many stars with masses well greater than 100 solar mass [6] [7] [8] , without trace of phenomena observed (such as strong gamma and X ray emissions), which are supposed to be associated with black holes. We analyze the properties of such loop currents on the 4D-5D boundary, where Maxwell equations are valid. We derive explicit expressions for the dipolar fields over the whole temperature range. We then compare our prediction with measured surface magnetic fields of many stars. Since there is coupling in distribution between the in-phase and anti-phase pairs of e-trinos, the generated magnetic field is directly related to the angular momentum, leading to the result that the magnetic field can be expressible in terms of only the mechanical variables (mass M, radius R, rotation period P)of a star, as if Maxwell equations are “hidden”. An explanation for the occurrence of this “un-expected result” is provided in Section (7.6). Therefore we provide satisfactory answers to a number of “mysteries” of magnetism in astrophysics such as the “Magnetic Bode’s Relation/Law” [9] and the experimental finding that B-P graph in the log-log plot is linear. Moreover, we have developed a new method for studying the relations among the data (M, R, P) during stellar evolution. Ten groups of stellar objects, effectively over 2000 samples are used in various parts of the analysis. We also explain the emergence of huge magnetic field in very old stars like White Dwarfs in terms of formation of 2D Semion state on stellar surface and release of magnetic flux as magnetic storms upon changing the 2D state back to 3D structure. Moreover, we provide an explanation, on the ground of the 5D theory, for the detection of extremely weak fields in Venus and Mars and the asymmetric distribution of magnetic field on the Martian surface. We predict the equatorial fields B of the newly discovered Trappist-1 star and the 6 nearest planets. The log B − log P graph for the 6 planets is linear and they satisfy the Magnetic Bode’s relation. Based on the above analysis, we have discovered several new laws of stellar magnetism, which are summarized in Section (7.6).
void of the stellar object, the existence of which is based on conservation/parity laws in physics if one starts with homogeneous 5D universe. While the in-phase e-trino pairs are proposed to be responsible for the generation of angular momentum, the anti-phase but oppositely charge pairs necessarily produce currents. In the 5D to 4D projection, one space variable in the 5D manifold was compacted to zero in most other 5D theories (including theories of Kaluza-Klein and Einstein [3] [4] ). We have demonstrated, using the Fermat’s Last Theorem [5] , that for validity of gauge invariance at the 4D-5D boundary, the 4th space variable in the 5D manifold is mapped into two current rings at both magnetic poles as required by Perelman entropy mapping; these loops are the origin of the dipolar magnetic field. One conclusion we draw is that there is no gravitational singularity, and hence no black holes in the universe, a result strongly supported by the recent discovery of many stars with masses well greater than 100 solar mass [6] [7] [8] , without trace of phenomena observed (such as strong gamma and X ray emissions), which are supposed to be associated with black holes. We analyze the properties of such loop currents on the 4D-5D boundary, where Maxwell equations are valid. We derive explicit expressions for the dipolar fields over the whole temperature range. We then compare our prediction with measured surface magnetic fields of many stars. Since there is coupling in distribution between the in-phase and anti-phase pairs of e-trinos, the generated magnetic field is directly related to the angular momentum, leading to the result that the magnetic field can be expressible in terms of only the mechanical variables (mass M, radius R, rotation period P)of a star, as if Maxwell equations are “hidden”. An explanation for the occurrence of this “un-expected result” is provided in Section (7.6). Therefore we provide satisfactory answers to a number of “mysteries” of magnetism in astrophysics such as the “Magnetic Bode’s Relation/Law” [9] and the experimental finding that B-P graph in the log-log plot is linear. Moreover, we have developed a new method for studying the relations among the data (M, R, P) during stellar evolution. Ten groups of stellar objects, effectively over 2000 samples are used in various parts of the analysis. We also explain the emergence of huge magnetic field in very old stars like White Dwarfs in terms of formation of 2D Semion state on stellar surface and release of magnetic flux as magnetic storms upon changing the 2D state back to 3D structure. Moreover, we provide an explanation, on the ground of the 5D theory, for the detection of extremely weak fields in Venus and Mars and the asymmetric distribution of magnetic field on the Martian surface. We predict the equatorial fields B of the newly discovered Trappist-1 star and the 6 nearest planets. The log B − log P graph for the 6 planets is linear and they satisfy the Magnetic Bode’s relation. Based on the above analysis, we have discovered several new laws of stellar magnetism, which are summarized in Section (7.6).
Keywords:
5D Projection Theory, Fermat’s Last Theorem, Perelman’s Mappings, Self-Rotation, Dipolar Magnetic Field of Stars, Laws of Stellar Magnetism, Laws of Stellar Angular Momentum, Magnetic Bode’s Law, Non-Existence of Gravitational Singularity, Semion State of Atoms in Stellar Surface, Magnetic Storm, Planetary Magnetic Field, Maxwell Equations at 4D-5D Boundary, Magnetic Fields of the Trappist-1 System

1. Introduction-Understanding Our Universe by Expanding the 4D Lorentz Manifold to the 5D Homogeneous Manifold and Project Back to the 4D Space-Time Structure via Two Projection Procedures
It is a very important step in physics to unify gravity with electrodynamics. Despite many trials, the past endeavors were unsuccessful. It is not correct to think that by adding another dimension to the Lorentz space-time, one can readily bridge gravity and electrodynamics. A unified theory along this line of thought therefore is not one that can be applied separately to a domain with masses in motion, and to another domain pertaining to dynamics of massless photons. The unified theory has to embrace both gravity and electrodynamics in an “inherent” manner. The general method we use is to analyze the physical properties of the universe via projection/mapping between the 4D and 5D space-time, with an analysis of the boundary conditions between the two domains.
In our model, after the absolute time , the universe is to be observed/ perceived. Since observation/measurement is realized after this absolute time instant, based on the uncertainty principle, the uncertainty of energy observed at
, the universe is to be observed/ perceived. Since observation/measurement is realized after this absolute time instant, based on the uncertainty principle, the uncertainty of energy observed at
this time is specified by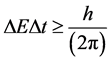 . Thus there is an infinite amount of
. Thus there is an infinite amount of
energy generated at this instant in the 5D manifold. The 5D manifold has to be homogeneous the reasons of which have been discussed in [1] . There is another reason: no physical laws have yet to be enforced. Some laws appear when the energy is perceived to be associated with e-trinos (conservation of spin, etc.).Other laws are realized when matter is being generated in the 4D Lorentz manifold. This time instant may be considered to be corresponding to the time when a Big Bang occurs in a Big Bang model discussed in literature. The term “Big Bang” in this paper therefore refers to the definition above according to the 5D theory. Starting with the above defined Big Bang concept, energy is flowing “out” along the radial direction in 4D space, and due to the Maxwell 4D boundary imposed, and any radial vector direction can become the Ricci Flow axis and generate beyond a finite 5D void core with a 4D Lorentz doughnut manifold. Since the choice of the Ricci Flow axis is arbitrary, hence many such doughnut Lorentz manifolds can be simultaneously created, thus completing the Big Bang picture of universe creation in the context of the 5D projection theory.
We assume the universe began with a homogeneous 5D space-time structure described by the above metric equation. From the homogeneous 5D manifold, we can apply projection operations [1] back onto the 4D Lorentz manifold, and requiring all the basic laws of physics to satisfy the known gauge invariance properties, so that there is consistency of mathematical logic steps linking variables in the 5D and 4D domains. We can then analyze and interpret the mathematically -deduced consequence and compare some aspects when appropriate measurable data are available.
The above projection reduction approach was presented in [1] , leading to the topological reduction of the homogenous 5D into the group representation of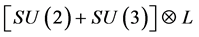 , where the L group represents the Lorentz 4D domain. It was emphasized that the resulting Poincare sphere, a “product” in projection, encloses an inhomogeneous 5D void in the center. Based on parity analysis, it has been remarked that massless spinors with equal amount of opposite charges must be present in such a void. In addition, vector potential, which gives rise to photons, must also exist inside the 5D void.
, where the L group represents the Lorentz 4D domain. It was emphasized that the resulting Poincare sphere, a “product” in projection, encloses an inhomogeneous 5D void in the center. Based on parity analysis, it has been remarked that massless spinors with equal amount of opposite charges must be present in such a void. In addition, vector potential, which gives rise to photons, must also exist inside the 5D void.
On the other hand, via the rigorous Perelman-Ricci Flow mapping [10] [11] , a homogeneous 5D is mapped into an inhomogeneous 4D doughnut structure. The consequence carries the important implication that there is a Beginning of space-time from absolute Nothing, and time is unidirectional, i.e. irreversible and the law of causality follows. This mapping procedure is then followed by Perelman’s entropy mapping [12] , via which the doughnut structure becomes a matter sphere satisfying the Lorentz manifold, thus proving Poincare’s conjecture [13] .
It is our intention to show the mathematical connections between these two mapping/projection procedures, as well as to investigate the physical outcome from such investigation in this paper, with special focus on the origin of magnetic field in the universe. Note that whatever method we employ to analyze the space-time structure of the universe, we always come up with a boundary separating the 5D and 4D domains. We start with the Fermat’s Last Theorem to analyze the space structure in the void and 4D-5D boundary in Section (2).In particular, we show that that breaking of the homogeneity of the 5D space-time, due to the imposition of the lower dimension 4D boundary, would lead to a time-frozen,  space domain, with concurrent matter formation surrounding the void. The 1D space structure is interpreted, due to parity, as an entangled state of two loops at the void-4D boundary. The generation of matter is restricted by charge parity. When the lightest lepton is generated, there must be equal amount of positive charge generated also. The generation of neutron does not violate such parity. Modification of the size of the current loop when neutrons are generated is analyzed in Section (2.3), putting forth the notion that generation of heavy elements can achieved in a similar way.
space domain, with concurrent matter formation surrounding the void. The 1D space structure is interpreted, due to parity, as an entangled state of two loops at the void-4D boundary. The generation of matter is restricted by charge parity. When the lightest lepton is generated, there must be equal amount of positive charge generated also. The generation of neutron does not violate such parity. Modification of the size of the current loop when neutrons are generated is analyzed in Section (2.3), putting forth the notion that generation of heavy elements can achieved in a similar way.
We pay special attention to the meaning and mathematical representation of homogeneity. Since other theories relating to transformation between a 5D domain and 4D domain have been published, we give a very shot review on the Kaluza-Klein (K.K.) [4] theory in Section (3). Also, we shall pay a revisit to the issue of gravitational singularity there. Note that Einstein’s unified theory [3] also followed the consequence of the K.K theory. One crucial difference between the K.K. theory, hence Einstein’s, and the present one here is that the 5D manifold of these theories are not homogenous, and the 4th space coordinate in the 5D domain is compacted to reduce dimension. We need to review this issue also because the 4th space variable in our theory is rotated to the radial direction during dimension reduction, together with the emergence of a current loop, (as a consequence of the space-space transformation) in the  boundary where Maxwell equations must satisfy. It is precisely the existence of this non- zero space variable, as a result of the Perelman entropy mapping (leading to a
boundary where Maxwell equations must satisfy. It is precisely the existence of this non- zero space variable, as a result of the Perelman entropy mapping (leading to a 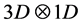 space structure) that provides the current loops that generate the intrinsic dipolar magnetic field in spherical stellar objects of the universe. Our analysis of the
space structure) that provides the current loops that generate the intrinsic dipolar magnetic field in spherical stellar objects of the universe. Our analysis of the 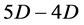 transformation leads us to conclude that there is no gravitational singularity in the universe.
transformation leads us to conclude that there is no gravitational singularity in the universe.
Explicit expression for the dipolar magnetic field of a general stellar object is derived in Section (4). Though the classical Biot-Savart law is employed, the quantum signature of the charge current is incorporated. The Three Laws of Dipolar Magnetic Fields of stellar objects, similar to the three laws of Stellar Angular Momentum discovered in [2] are also presented with numerical illustration in the same section there. Moreover, we have derived the ratio of the dipolar magnetic field strengths when the matter shell is composed of either (i) pure hydrogen ions, or (ii) purely Helium ions as two examples based on quark mass analysis during the generation of matter based on the dimension projection theory. As the mass density within the shell increases, the 3D space homogeneity of a shell near the surface is broken into . The variation of gravity is approximately only along a direction perpendicular to the local plane on the surface. It is this broken space that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state in which the electron collapses into the proton environment, bringing with it the pinned magnetic flux. We explain in Section (5) how the consequence, qualitatively, of the formation of such Semion state could lead to the generation of huge sporadic magnetic field from the stellar surface when the 2D state changes back to the 3D state, as part of the stellar evolution process. To test the general validity of the dipolar field equation we have derived, we introduce in Section (6) a new method of graphical analysis using measured values of the basic set of data (mass, radius, rotation period), and compare the power indices of the relevant variables. Very satisfactory results has been obtained for 8 different star groups: (6.1) the pre-main-sequence stars in the Orion Nebula; (6.2) the NGC 6819 stars; (6.3) the mid-to-low mass stars of the main sequence; (6.4) the pre-dwarf M34 stars; (6.5) the NGC 2516 stars; (6.6) brown dwarfs; (6.7) white dwarfs and (6.8) magnetic white dwarfs. There are two features in astronomy related to stellar magnetic field which are like mysteries. One is the linear relation between surface magnetic field
. The variation of gravity is approximately only along a direction perpendicular to the local plane on the surface. It is this broken space that leads to the atomic binding from Bohr to Chern-Simons hydrogen solution. In the relativistic limit, the Chern-Simons solution is given by the Semion state in which the electron collapses into the proton environment, bringing with it the pinned magnetic flux. We explain in Section (5) how the consequence, qualitatively, of the formation of such Semion state could lead to the generation of huge sporadic magnetic field from the stellar surface when the 2D state changes back to the 3D state, as part of the stellar evolution process. To test the general validity of the dipolar field equation we have derived, we introduce in Section (6) a new method of graphical analysis using measured values of the basic set of data (mass, radius, rotation period), and compare the power indices of the relevant variables. Very satisfactory results has been obtained for 8 different star groups: (6.1) the pre-main-sequence stars in the Orion Nebula; (6.2) the NGC 6819 stars; (6.3) the mid-to-low mass stars of the main sequence; (6.4) the pre-dwarf M34 stars; (6.5) the NGC 2516 stars; (6.6) brown dwarfs; (6.7) white dwarfs and (6.8) magnetic white dwarfs. There are two features in astronomy related to stellar magnetic field which are like mysteries. One is the linear relation between surface magnetic field  and equatorial rotation speed v in the log-log graph, and the other is the so-called “Magnetic Bode’s Law” which simply states that the parameter BsR3 and Iω relation is also linear in a log-log plot, particular for cool stars; here
and equatorial rotation speed v in the log-log graph, and the other is the so-called “Magnetic Bode’s Law” which simply states that the parameter BsR3 and Iω relation is also linear in a log-log plot, particular for cool stars; here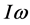 is the angular momentum. Though we have carried out a very detailed analysis of the B-v relation in Section (6) for many star groups, no suitable complete measured data sets
is the angular momentum. Though we have carried out a very detailed analysis of the B-v relation in Section (6) for many star groups, no suitable complete measured data sets  have been obtained for every star in these star groups in Section (6). Such a set of four variables for each individual star in the sun-like group with over 100 members have been published. We apply that in Section (7) to analyze the stated two mysteries. The study there is important because on face value, no parameters related to electric current are involved in the stated two relations. Where are the Maxwell equations “hidden” behind such Laws? Whereas other scientists have attempted to explain these features using various forms of dynamo theories, we find that our derived expression for the dipolar field can automatically explain such phenomena, implying that based on the 5D-4D projection theory, the co-existence of in-phase and anti-phase spinor pairs circulating in the stellar void can automatically explain the origin of angular momentum and the origin of dipolar magnetic field in stellar objects at the same time. Section (7.5) is devoted to compare the difference of the theoretical prediction and measured values of the dipole fields of some members of our planets. Section (7.6) is a summary of the laws and issues discovered in this paper. Section (7.7) concludes our endeavor. The numerical values of the relevant variables/parameters to be applied in our numerical study in this paper are all based on the fundamental well-established constants, such as electron mass, quark mass, electronic charge, the Planck constant, plus data measured only―there is no other input parameter and no parameterization process involved.
have been obtained for every star in these star groups in Section (6). Such a set of four variables for each individual star in the sun-like group with over 100 members have been published. We apply that in Section (7) to analyze the stated two mysteries. The study there is important because on face value, no parameters related to electric current are involved in the stated two relations. Where are the Maxwell equations “hidden” behind such Laws? Whereas other scientists have attempted to explain these features using various forms of dynamo theories, we find that our derived expression for the dipolar field can automatically explain such phenomena, implying that based on the 5D-4D projection theory, the co-existence of in-phase and anti-phase spinor pairs circulating in the stellar void can automatically explain the origin of angular momentum and the origin of dipolar magnetic field in stellar objects at the same time. Section (7.5) is devoted to compare the difference of the theoretical prediction and measured values of the dipole fields of some members of our planets. Section (7.6) is a summary of the laws and issues discovered in this paper. Section (7.7) concludes our endeavor. The numerical values of the relevant variables/parameters to be applied in our numerical study in this paper are all based on the fundamental well-established constants, such as electron mass, quark mass, electronic charge, the Planck constant, plus data measured only―there is no other input parameter and no parameterization process involved.
2. The Meaning of Spatial Homogeneity & Application of the Fermat’s Last Theorem to the Boundary of the 5D-4D Domains
2.1. Basics of the Special Properties of the 5D, 4D Domains and the 5D-4D Boundary
As we proceed through the paper, the physical properties of the 5D-4D boundary are of crucial importance; we therefore need to high-light some basics, which are consequence of the projection theory and fundamental physics.
a) From the 5D homogeneous metric, one can obtain a 5D second order energy-momentum differential operator without a term pertaining to mass. Solutions of such metric equation represent 5 vector potential fields (including charge-source terms, thus existence of e-trinos) traveling with speed c, similar to the fields associated with the Maxwell potentials in the 4D Lorentz manifold. In the 5D domain, a term pertaining to magnetic monopole exists. In 4D domain, the electric, magnetic symmetry is broken, so that there is no magnetic-mono- pole term in Maxwell equations.
b) In a 5D domain, a Dirac linearization process does not lead to mass creation via projection/mapping, implying the e-trinos must be massless, but charged. These spinor states are equivalent to magnetic monopole states in 5D. In 4D domain, a Dirac linearization process leads to solutions representing the state of massless, charge-neutral neutrino and the state of massive charged lepton (described by the SU(2) group) in pair form.
c) Based on (a) & (b), the states of e-trinos and 4D Maxwell potentials must form the boundary between the 5D & 4D homogeneous manifolds, implying that both classical and quantum representations are allowed in the boundary. A satisfactory quantum theory should also have such representations.
d) The void space is expressed as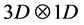 , with time frozen, meaning that the pair spinor states in 3D are orthogonal to those in 1D structure. When a pair is charge neutral, it must be in 3D space, as the product
, with time frozen, meaning that the pair spinor states in 3D are orthogonal to those in 1D structure. When a pair is charge neutral, it must be in 3D space, as the product 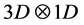 gives the Maxwell potential after a Dirac linearization process; hence such spinor pairs generate a net angular momentum
gives the Maxwell potential after a Dirac linearization process; hence such spinor pairs generate a net angular momentum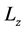 . The remaining 1D space, being orthogonal to the 3D space, then must contain no net momentum. However, similar to the appearance of the monopole term in 5D Maxwell equations, the 1D space carries a current of magnitude 2ec, which results from
. The remaining 1D space, being orthogonal to the 3D space, then must contain no net momentum. However, similar to the appearance of the monopole term in 5D Maxwell equations, the 1D space carries a current of magnitude 2ec, which results from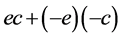 . If such a current forms a ring or loop, with a single frequency
. If such a current forms a ring or loop, with a single frequency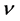 , then these charges will produce a magnetic dipole field, but could annihilate, and cannot remain in a perpetual state. Because the 3D space is symmetric, such a current pair loop must be split into 2 parity states in two different magnetic latitudes, one in each hemisphere. Since the 2 parity loops produces the same in line magnetic field, they will give a pure dipolar field similar to a bar magnet. The general charge neutrality within the 1D domain implies that it is possible to break the neutral charge condition between hemispheres, as long as their sum neutrality is maintained. A more detail discussion later in relation to the conformal projection P1 of these spinor states on the creation of quarks and thus hadrons will be given.
, then these charges will produce a magnetic dipole field, but could annihilate, and cannot remain in a perpetual state. Because the 3D space is symmetric, such a current pair loop must be split into 2 parity states in two different magnetic latitudes, one in each hemisphere. Since the 2 parity loops produces the same in line magnetic field, they will give a pure dipolar field similar to a bar magnet. The general charge neutrality within the 1D domain implies that it is possible to break the neutral charge condition between hemispheres, as long as their sum neutrality is maintained. A more detail discussion later in relation to the conformal projection P1 of these spinor states on the creation of quarks and thus hadrons will be given.
e) According to the P1 projection, the 4th space coordinate of e-trinos in the 5D manifold is conformally mapped into quarks of fractional charges. In order to produce a proton (composed of (u, u, d) quarks) and a neutron (composed of (u, d, d) quarks), as an example, we need 3 up and 3 down quarks. Since the 3 up quarks have a total charge of 2e, they are projected via the P1 process from 2 e-trino loop states of one loop. As the 3 down quarks have a total net charge of -e, they can be produced by P1 from just 1 anti-e-trino state from the other loop. To balance the + e charge resulting from the stated P1 projection, the Po projection on an in-phase pair (on the void surface) gives a lepton, such as an electron (exists in Lorentz space L), due to SU(2) symmetry and the unidirectional nature of time in the 5D metric. Effectively, we say that the consequence of Po is specified by the group product . We have overall charge neutrality in the universe all the time.
. We have overall charge neutrality in the universe all the time.
f) After the entropy mapping, or equivalently the combined Po and P1 mapping, we have a spherically shaped mass stellar object model enclosing a 
where p, e ,s represent the momentum, charge, and spin respectively. The in phase circulation of the oppositely charged massless spinors (with spin degeneracy



g) In this paper, we analyze the consequence of the out of phase rotating of the spinor pairs specified by the following four state groups:
In the calculation of current, these four states lead to the spin degeneracy factor 
2.2. The Fermat’s Last Theorem and Space Time Metric
Detail of the 4D Maxwell boundary can be explicitly analyzed through Fermat's theorem, in terms of Abelian angles. The Fermat’s sum of quadratic coordinate components has been proved to be rigorous for any number of coordinate dimensions [5] .
Leonhard Euler in 1770 [15] was the first to prove that for all non-zero 




In fact, we put forth the notion that n = 2 is the only condition that 

By expanding the Lorentz manifold to the 5 space-time, we learn that the universe has a homogenous 5D space-time structure described by the metric

where 

In the homogeneous 5D space-time, all 4 orthogonal space axes are exactly equivalent. Thus each axis has a measure r' as represented in the complex phase angle O(1) group [18] . This group has three elements specified by angles 












Since the solutions of a differential equation is totally governed by the boundary conditions that are imposed, the vector and massless charged spinor solutions to the 5D homogeneous metric operator equation are dictated by the 4D Maxwell space-time boundary which forms the enclosure to (or embracing) the 5D manifold. At the absolute time t, the space volume of the homogeneous ND manifold must have a boundary enclosure of





Since the determination of the Ricci Flow direction for the 

Our remaining problem is the general spherical shape of the massive stellar objects observed within each galaxy satisfying the Poincare Conjecture. To illustrate this topological mapping process, Perelman introduced an entropy mapping [12] , which basically closes the doughnut 5D core, into a void that contains a 3D spherical volume plus a 1D closed loop that is orthogonal to the 3D radius; this 1D loop must be on the surface of the spherical volume. Comparing projection theory and Perelman’s theory, the 3D radius of the void, is defined by the Po projection of the 4th space coordinate. This consequence is similar to that of the Ricci Flow mapping, except the matter domain totally encloses the 5D manifold. The physical state of this void is time frozen at
2.3. Modification of the Size of the Current Loop When Neutrons Are Generated
We note again that in the 5D manifold, there are 5 vector potential components (instead of 4 in the Maxwell domain), and 2 massless spinors with charges e and -e. [Section 2.1]. In order that these solutions satisfy the boundary conditions imposed by the Maxwell domain, we need to transform the 5 component symmetric vector potentials into the 4 Maxwell vector potentials by breaking the symmetry of solution as carefully illustrated by Maxwell in his thesis, with the emergence of a magnetic mono-pole potential, which corresponds to the 5th component vector potential in the 5D manifold. [21] [22] [23] .
We will find an explicit expression for






While the current loop


Combining these two representations, & letting


which determines the geometry of void boundary.
The rotation of 










Therefore, 





This is the size of the current loop if a pair of electron and proton is generated simultaneously; in other words, hydrogen atom is generated.
Note that charge, linear momentum, angular momentum, and energy must each be conserved during the generation of matter. We have only the lightest lepton and quarks generated initially, before the gluon potential is in action to produce proton and neutron. A set of (u, u, d) of quarks must be generated (to build up eventually a proton) together with the generation of an electron, according to the 5D projection theory. The gauge requirement for the solution on quark spinors is the charge to mass ratio


where 



Since mass is generated from nothing, the uncertainty principle requires that

(as a minimum); where 

where 
Using the data for




However, there is also the factor due to the reduced-mass effect of the proton-neutron pair, and the reduced mass 


Hence, effectively, the time to generate a proton-neutron pair is longer than generating two protons by a factor of 2.225. Now many electrons and protons are generated simultaneously, while the 5D void is expanding until the mass shell is generated. Thus, the void radius 



if the mass shell is composed of helium four. If the matter crust is composed of hydrogen and Helium 4, the factor b would be
With expressions (2.3.2) & (2.3.7), we can apply the magnitude of the current loop to calculate the magnetic field generated by such a loop. Before we do the application, we have to derive an explicit representation of the magnetic field generated such a current, one near each magnetic pole, when the particular element(s) is considered to be existing at the Lorentz space-time and void boundary. Such derivation will be carried out in Section (4). At the meantime, we need to analyze in the next Section about the origin of the “key” variable 
3. Proof of Non-Existence of Gravitational Singularity in the Universe
3.1. The Crucial Difference between the Kaluza-Klein 5D Theory, Einstein’s Unification Field Equation and Consequence of Perelman’s Two Mappings
The original Kaluza-Klein theory (KK theory, see e.g. review in [4] ) was an attempt to develop a field theory which could unify all the forces under one fundamental law. In the framework of the theory, distance squared between the two neighboring space points 



where the usual summation rule is understood, and 



Equating (3.1.1) to (3.1.2) gives

where

is called the vielbein. For a non-uniform gravitational field, the KK theory introduces the notion that “At every point in a reference frame with an arbitrary gravitational field it is possible to choose a locally inertial (freely falling) reference frame.” In other words, like carrying operation using the concept of calculus, the flat Minkowski metric can be transformed into a curved space-time metric. However, we would remark that in Equations (3.1.3a) & (3.1.3b), it was already assumed that a gravitational field is present due to the presence of the Riemannian tensor. This assumption implies that in the domain considered, mass exists. Thus the 4D is a Lorentz manifold, and by an extension to 5D space- time, such a 5D structure would not be a homogeneous 5D. Hence the Ricci- Flow mapping does not reduce this 5D back to 4D, except simply by closing the extra 4th space dimension into a closed loop.
Without going into further details, we would remark that both the KK theory and Einstein generalized field equations have difficulties to explain experimental data and interpret mathematical singularity: (i) In order to exclude the singularities in the equation set, both K.K. and Einstein introduced the method of compactness. Such an assumption leads to the models of black hole, and dark matter, which to us, are not necessary.; (ii) The electron charge e and mass me are included in a certain constant κ in K.K. theory which bridges the electromagnetic potentials and some metric tensor components including the 5th dimension. The values of both e & me deduced based on the KK theory (or Einstein’s field equations) were not consistent with the well-established experimental values then (see comments in [4] ); (iii) The KK theory (and Einstein unified field equations, [3] ) did not contain any of the nuclear forces; during that time there was lack of experimental data from accelerators and the corresponding concept in particle physics.
Concerning the key difference between their theories and projection theory developed in this series, we need to note that in KK theory, as well as Einstein's 5D metric, the proper time τ is not connected to the 4th space dimension variable. Therefore, the KK 5D is not homogeneous, neither is mass a result of space projection.
3.2. Absence of Gravitational Singularity
As analyzed in Section (2), the 1D space within the Poincare matter sphere is a set of two closed loops that includes the 



Assuming a uniform mass distribution in a plane with the 2D void region bounded by

where













Moreover, the finding of a 


Having analyzed the concrete role played by the space variable 
4. Explicit Expression of the Intrinsic Dipole Magnetic Field Generated by Current with Quantum Signature at the 5D-4D Interphase
4.1. Quantum Current Density of the Ring Current in the Void Boundary
During the deduction of the three laws of angular momentum in [2] , we have not included those spinor pairs circulating out of phase. They do not produce a net angular momentum, but they produce a net electric current generated by the (e, p; -e, -p) massless spinor pairs within the 
As these charges build up a stationary/perpetual current state, the wave function of a spinor pair represented by the symbol 

where 




Now for non-relativistic particle with mass m moving along a circular orbit so that differentiation with respect to space variable is one-dimensional, we use the symbol 

Since the spinor e and spinor?e are two distinguishable particles, in carrying the thermal averaging process later on, we need to calculate the number N for either type of spinors. The electric current, however, is doubled, because they are circulating out of phase in the classical sense. Therefore the overall current density in one ring is finally

We have left our sign convention in deciding the magnetic polarity, as the sign convention is very simple. We have fixed the “classical current” to be one dimensional, 




Remark again that the subscript 2 signifies that the 1D space structure has an entangled structure of two loops, composed of both e & -e spinors as explained in Section (2). Note that 



The electrodynamics of charged massless particles moving with velocity c is not at all explored much within the frame work of Maxwell equations and the frame work of quantum field theory. An insightful investigation of the exact solution of such particles in Maxwell equations has recently been published [26] . Explicit expressions for the vector potential and the electromagnetic field were derived under the following conditions of motion of the charged massless particles: (a) linear, (b) accelerated unbounded, (c) accelerated bounded. However, unless the model charge is attached to a string (as in string theory), usually there are singularities in those solutions.
First, we would emphasize that we proposed that the existence of the massless charged spinors are represented by solution(s) of the 5D metric, rather than the 4D Maxwell potentials generated from classical massless charged particle. In fact, if the spinor solution is obtained from the massless 4D Dirac equation, with the introduction of charge, such solution must be coupled to the Maxwell potentials, and the coupled equation(s) cannot satisfy the Lorentz gauge transformation without a string attachment. Yet when this hypothetical string is reduced to zero, singularities appear in the Maxwell solutions.
It might be simple to analyze the gauge invariance property for charged massless spinor in 4D by applying the projection of the metric from 4D onto 3D (as explained in [1] ). In this case the Lorentz gauge is changed to the Chern-Simons gauge [31] . To investigate whether a massless spinor moving with c can exist in the 4D metric, let us consider the hydrogen system, where the electron is assumed to be massless. This system has a Semion ground state [32] with binding energy equal to the reduced mass, which is then zero, implying such a ground state does not exist. In general, massless charged spinors cannot be bounded in 4D Maxwell space-time. The solutions found in [26] by attaching a string, is precisely found by addition of the 4th space dimension (making the system a 5D manifold), so that a finite confinement can occur in the (added) 4th space dimension. Hence if we extend the Maxwell 4D to

And the current over the ring is

In passing, we would note that even if there were e & -e charges circulating in opposite directions along the 1D classical current ring, the chance of annihilation is non-zero. In general, the interaction cross-section of massive particles is larger than those of massless particles, such as photons. In fact, the strength of interaction of photons with massive particles depends strongly on the masses of the interacting particles. The cross-section area of a charge-neutral neutrino is well known to be extremely small, so that equipment to detect neutrinos is set in gold mine deep down underground. It has been estimated that there is only an upper limit on the mass of neutrino




4.2. Simple Representation of the Magnetic Dipolar Field Generated by the Classical Ring Current Model with Quantum Signature Incorporated
A charge current generates magnetic field in space. The Biot-Savart Law expresses the magnetic field in terms of the magnitude, spatial length, direction, and the distance from a reference point (such as the center of a ring current) of a current. According to this law, the magnetic induction field generated by a charge current density J at the space point x is

Using elementary vector analysis,

When the distance between the coordinate origin and the point of observation is much greater the radius of the model ring current, i.e. 


Here 

where 



the statistically averaged energy is

From (4.1.6),

In view of the derivation in Appendix A, we obtain

Then from (4.2.2b), the magnetic filed measured at the equator of the matter star 

This equation may be called the Law of Intrinsic Dipole Magnetic Field for Stellar Objects.
Before we proceed to obtain numerical values to illustrate the laws we discover related to the origin of the intrinsic dipolar magnetic field of stellar objects, we need to find explicit expression of

Through computer program, using Simpson’s rule of integration, the integral 













We now plot the I versus T graph, since 
Such that




For even greater temperature such as

to good approximation. The straight green line in Figure 1 with a constant positive slope represents such a line.
On the other hand, if the temperature is relatively low, such that

In Figure 1, the integral in this region is represented approximately by a redhorizontal line. The intersection of the above two straight lines cross at the
Figure 1. The integrand, as depicted in expression (4.2.7), is a function of temperature T (K). The straight green line with a constant positive slope represents the approximate solution given by Equation (4.2.8b). The red horizontal line represents the approximate solution indicated by Equation (4.2.9). The two straight lines intersect at. T = 3.2 ´ 109 K. We observe that the stated approximated solutions in the “low/cold” and “high/hot” temperature ranges are very good.
temperature
We would emphasize that integral 
can also be separated into two regions in temperature. Under the First Law of the angular momentum, i.e.

In view of Equations (4.2.8b) & (4.2.10), we obtain the Law of Intrinsic Dipole Magnetic Field for Hot Stars below:

As P&R are dependent implicitly on T, when T is large, P is small, and one has to carry out detailed numerical analysis before one can learn how B(eq) varies with T in realistic samples. Moreover, all the equations for B(eq) hold under the condition of
equally complicated. Here we want to emphasize that
can be separated into two regions in T. At small T and large T, the asymptotic lines are respectively two straight lines (one horizontal, and one with positive slope) intersecting at 


right away that 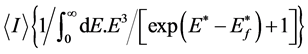
cool region. Inspection of (4.2.11) reveals that therefore B(eq) depends explicitly only on the mechanical variables in front of the quotient of the state two integrals. This is a very crucial aspect of our discovery.
Under the regime of the Second Law of angular momentum, we present in Appendix B, the approximate expression of statistically weighted over
and Equation (4.2.9) already gives the approximate expression for the integral

where

Recalling that

We may call Equation (4.2.12) as the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. This equation will be used throughout the numerical analysis in this paper.
We have deduced the magnetic expression understand the Second Law condition because we are interested in finding the dipole field when the matter shell has been formed and the temperature of the void-matter boundary is not too high 
5. On the Plausible Origin of Huge Non-Dipolar Strong Magnetic Fields of Many Stars, Including the Old/Dying Ones
It has been shown that the Maxwell and Chern-Simon gauge theories are coupled/compatible and the charge flux pinning phenomenon can be realized by the Maxwell-Chern-Simons gauge theory in a 2D system [31] [32] [33] .
Now the confinement of a 3D hydrogen to a 2D state is supported by the fact that exact analytical solutions for 2D hydrogen can be derived for the non-relati- vistic and the relativistic H-atom model [34] [35] . From the view point of the Bohr’s model, the exact solutions for the relativistic ground state of the 2D-hy- drogen atom gives a binding energy as large as the reduced mass of the composite system [34] . The consequence is that the binding energy plus the rest energy of the system can become zero if the positive charge (the center of attraction) is much more massive than the electron. In other words, a 2D or collapsed hydrogen atom hydrogen atom can approach a Semion state, with magnetic flux attached to every electron [33] .
When a star has a large mass (such as the sun) and a small radius (such as the terrestrial radius), a large gravitation gradient exists along the radial direction, confining the motion of electrons from a 3D space to a 
From the symmetry point of view, we say that the 3D space homogeneity is broken into










via simple expansion of



Hence for non- zero h values, the gravitational potential difference 









Let us take some concrete examples. It is well-known that magnetic storms are found to be periodic on the solar surface. We anticipate that the solar motion participates in the occurrence of periodicity. Thus if the gravitational potential difference (as a matter pressure) is the cause of Semion states formation, such states are likely to be formed slightly below the photosphere. Cyclic plasma turbulence could bring the Semion states to the surface, and the 
We would note also that the star will be positively charged and would attract negatively charged particles with low kinetic energy. Note for small stars such as Magnetic White Dwarfs

Let us “borrow” some result in condensed matter physics to estimate the magnitude of magnetic field generated by a group of Semions. The 2D number density of composite fermion system σ is related to the magnetic field B by (see e.g. [31] )

where n is the “level” of quantum flux and 
Suppose for rough estimation, let us take a magnetic white dwarf WD0011134 associated with the set of data




taking the level n = 1 as the upper limit of the magnetic field B estimation. The 2D density of Semion, from Equation (5.2), is therefore

If Semions in the whole surface layer have enough energy to overcome gravitational and Coulomb attractions, the average magnetic field (which is radial in directions) over the whole stellar surface, being hypothetical released is then

It is known that the magnetic fields of Magnetic White Dwarfs are non-dipo- lar and distributed irregularly [40] . Thus to produce a magnetic field of 



Note that this final stage of the star still possess the 



6. Analysis of the Variation of the Theoretically Derived Dipole Magnetic Field with Respect to Change of the Basic Features of a Star
6.1. Introduction with a Set of Data of the Halo Stars in the Orion Nebula
We have derived the equatorial magnetic surface field in terms of the basic/“raw” data set (M, R, P):

We define the set of variables (M, R, P) as the basics/raw data variables. In some stars, all the three variables can be measured, but the number of such stars is small, and the accuracy of measurement is left with some high degree of uncertainty. In some star groups, the radius can only be theoretically deduced; a typical example is the application of the Hamada-Salpeter equation [41] to obtain the radii of (cool) dwarf stars with values of mass as input data. The above expression is valid only when the angular momentum is equal to that of a solid sphere with the same mass density, as a zero-order approximation. In stars, the matter sphere is built of magnetized plasma while fusion processes proceed to build up heavier elements. Eventually, we have neutron stars as briefly sketched in [2] . Essentially, therefore the three basic variables are inter-connected. We will leave the more detailed discussion on the laws we discover in the next section. As the rotation periods of pulsars have been observed to be slowed down continuously, and such an aspect is intuitively true from the consideration of energy conservation, obviously the B-P relation of different star groups would bring us useful information in stellar structure and stellar evolution. Therefore, we focus on the variation of the equatorial/polar field with respect to changing period of rotation first. We remark that the normalized void radius 

So we begin with the pre-main ?sequence or hollow stars of the Orion Nebula. Data of these stars in the Milky Way are taken from [42] . Here the mass






Figure 2(a) and Figure 2(b) show the B(equatorial)-P graphs for the density ranges of 48 - 100, and 100 - 160 


Figure 2. (a) The surface equatorial magnetic field B (eq, Gauss) vs the period of rotation P(s) for stars in the Orion of the Milky Way with mass density between about 48 to 100 kg/m3. The one off star is reported to have a radius of 3.23 solar radii, and consider that is out of the group. The correlation is over 0.9 if we take off this “off-line” sample. We keep it there to show that when the density is too low, the B-P relation is deviated from linear in the log-log plot. The maximum of horizontal axis is 106 s. See data in Table 1; (b) The surface equatorial magnetic field B(eq, Gauss) vs the period of rotation P(s) for stars in the Orion of the Milky Way with mass density between about 100 to 160 kg/m3, using data in Table 1. The correlation is good and power index is −0.69. Though the correlation is good, further analysis as shown in the text indicates that the comparison between theory and experimental data is not simple, and several steps are needed, and the methodology becomes clearer as we go through the other sub-sections following.
Table 1. Data of the pre-main-sequence stars in the Orion Nebula in the Milky Way are taken from [42] . Here the mass







sity of the stars in Figure 2(a) is very low, and we neglect the mathematical analysis. The B-P plot in Figure 2(b) for stars with density in the range of about 1.0 - 1.6 

Substituting (6.1.2) into (6.1.1), we arrive at

Or

Further analysis shows that there is no clear mathematical relation of the P-R plot, nor the P-M plot, using the raw data. In other words, we cannot compare the theoretical prediction and experimental relations for this group of stars. Such a result is to be expected, because they are halo stars and the theory assumes that the angular momentum expression to be represented by
6.2. NGC 6819 Stars
We proceed with another group of stars with larger density, since the magnitude of B is sensitive to density values. Parameters include mass M in units of solar mass





Table 2. Some parameters of stars in NGC 6819. Parameters mass M in units of solar mass










First, we plot the B − P graph in log scale using the measured basic variables (established expression like mass-radius relation for dwarfs). Figure 3 gives such a graph with a negative slope of −0.584. Equation (6.1.1) can then be written as

Since the correlation is very good, we can assume that

is valid, and Equation (6.2.1) becomes

Since the stars are associated with various values of the sets (M, R, P), if Equation (6.2.2) is to be approximately true, these variables must vary in such a way that the function F1 is approximately a constant. We plot in Figure 4 the values of F1 for these 30 stars using the raw data from Table 2. There are some fluctuations, but in a rough way, we can proceed to analyze Equation (6.2.3), taking F1 as a constant.
Figure 3. The variation of the theoretical surface magnetic fields B (eq, theory, Gauss) of NGC 6819 stars with changing period of rotation P(s), according to the 5D theory. The data are taken from numbers entered into Table 2. The slope of the log-log plot is about minus 0.584.
Figure 4. Values of the function F1 for 30 stars in NGC 6819. The upper horizontal line represents the value 3.0 ´ 108. The average of these 30 numbers is about 2.5 ´ 108 (SI units).
Equation (6.2.2) can then be approximated by:

Or

Employing raw data from Table 2 for different star members of the NGC 6819 group, the graph of log P against log R is linear with a slope of -3.76 (see Figure 5), so that Equation (6.2.4b) can be expressed as

Or

Or

Note that the above equation is the consequence of the theoretically derived Equation (6.2.1), with the use of the P-R relation from measured data. To test the validity of the theory, we now use the raw data sets (M, R) from Table 2, and plot their relation in Figure 6 below. This graph gives a power index of 1.0612. Observing that there are variations of data of this group of stars with density several hundred of

Following, Figure 7 shows the variation of the theoretical surface magnetic fields B (eq, theory, G) of NGC 6819 stars with changing values of the void radius


Figure 5. Employing raw data values in Table 2, this graph shows the variation of the period P with different values of the radius R for different star members. The slope of the above graph is −3.761. The maximum of horizontal axis is 2 ´ 109 m.
Figure 6. The Mass?radius relation using raw data from Table 2. The slope of the power relation is 1.0612. As a very rough estimation, we predict from theory that the slope of the log M-log R plot is 1.168. The maximum value on the horizontal axis is 2.0 ´ 109 m.
Figure 7. The variation of the theoretical surface magnetic fields B (eq, Gauss) of NGC 6819 stars with changing void radius 
stars have larger void radius Ro when the mass density is low, suggesting that gravity contraction causes the void size to decrease, but at a very slow rate because the value of the slope is not far from unity. We would investigate whether such effect is similar to other star groups, and the power index should in principle, indicative of the mass of the stars involved. As suggested by the crowing of data points in Figure 3 and Figure 8, we could have divided these 30 stars into two sub-groups according to density. Since the NGC 6819 stars have density up to 
Figure 8. Void radius 


6.3. Low to-Mid Mass Main Sequence Stars
We follow up to study the B - P graph for Low-to-Mid mass main sequence stars. Parameters mass


Following the argument of the previous sub-section, we can take that the function

is approximately constant, and the above equation gives 


Since the M vs R plot is a good straight line with positive slope β = 1.0985(Figure 10), we can write (6.3.3b) as

We require
Or

If one plots the P-R graph (not shown here), the line of best fit has a very large positive slope(specified by angle

Figure 9. Employing values in Table 3, theoretically deduced equatorial dipolar magnetic field B (eq, Gauss) against rotation period 

Figure 10. The measured variation of mass M (kg) with respect to change of radius R of some members of the Low-to-Mid Mass main sequence stars (see Table 3). The power index is about 1.0985 here, as compared to the theoretical prediction value of 1.1; see details in Section (5). The maximum of the horizontal axis is
Table 3. Low-to-mid mass main sequence stars. Parameters mass



group in the following Figure 11. The constant A for 12 stars with 

With the establishment of (6.3.6), we also deduce that

Likewise, we obtain


The result of Equation (6.3.9) is shown in Figure 12. Note that as explained in Section (2.3), the void radius Ro and hence current loop size depends also the type of elements generated in the matter shell at the time of observation.
Figure 11. According to our theory, 


Figure 12. Employing values in Table 3, theoretically deduced equatorial dipolar magnetic field B (Gauss) against void radius 
Among this group of stars, we cannot expect all the star samples are built of hydrogen only. Thus the correlation of 0.83 in Figure 12 refelects the stated variation, and in our opinion, such correlation is already high in astronomy studies.
6.4. M34 Stars
M34 stars are pre-dwarfs having mass density slightly greater than that discussed in the last sub-section. Basic data are taken from [47] and other relevant variables are calculated and listed in Table 4. Taking M34 stars within a mass density range of 


Using raw data from Table 4, the M-R relation is shown in Figure 14, giving a slope of 0.9169. Substituting equation 

So far, we can say that Equation (6.4.2) is a consequence of the derived Equation (6.1.1) with input of raw data. The P-R plot in log scale (Figure not shown) from raw data shows a slope of ~5, supporting Equation (6.4.2) though the
Table 4. Stars of the M34 group [47] . The equatorial magnetic fields B (Gauss) are calculated according to the theory of Section (5) of this paper. The deduced values of the magnetic parameter 




*this datum was observed under poor condition.
Figure 13. The equatorial magnetic field B (eq, Gauss) vs 

Figure 14. Mass vs radius of 12 pre-Dwarfs of the M34 group within a rather wide mass density of

points are relatively scattered, due to large variation of the mass density among these samples. Just as that demonstrated in the last sub-section, if we have enough samples of narrow density range, the agreement between theory and measured result would be much better. Following, we plot the D-R graph in Figure 15. The negative slope indicates that the smaller the star, the higher the density, implying that in the star group more elements are formed in smaller sized stars, increasing the gravity force which leads to a smaller radius. This feature is characteristic of pre-Dwarfs and Dwarfs.
6.5. Averages of 254 Stars in the NGC 2516 Group
NGC 2516 is an open star cluster in the southern sky, also called Southern Beehive [48] . Following the same method as in other groups, basic data are taken from [49] and other variables are calculated, listed in Table 5. The B-P graph indicated in Figure 16 can be represented by the equation

Substituting Equation (6.5.1) into (6.1.1), we have,

This function F5 has been found numerically to be 

which becomes
Or

From (6.5.3) & (6.5.4), we obtain an equation relating M and P resulting from theory (with information from basic data only):

Figure 15. Mass density vs radius of the same 12 pre-dwarfs M34 (as in Figure 14) within a wide range of density. The maximum of the horizontal axis is
Table 5. Five data set representing 254 Low massstars in NGC 2516.





Figure 16. 254 Low massstars in NGC 2516. The equatorial magnetic fields B (eq, Gauss) is plotted against the period of rotation 
We use the basic data from Table 5 to plot the P-R graph &M-R relation in Figure 17 and Figure 18 respectively; these graphs have power indices of 3.3721 &1.349 respectively. The agreement of the M-R relation between theory and experiment (1.37 vs 1.349) is amazingly close, noting that only three significant figures have been used in computation.
In the following Figure 19, we show the dependence of B (eq, theory, Gauss) on void radius


Figure 18 is relatively large, being 1.3487, suggesting material is being added on the star with M& R increasing at the same time. It is interesting to note that the power index is only 0.4123. We expect for Dwarfs, such an index in the 
6.6. Brown Dwarfs with Effectively 1353 Star Data
Nine sets of raw data, each representing an average of 150 stars are entered into Table 6. Effectively we have averages of 1350 brown dwarfs. In addition, we add another three sets of data for three brown dwarfs with relative fast rotation speeds according to ref [50] [51] [52] and [36] .
As shown in Figure 21, the power index 

This constant F is found to be about 

which becomes
Figure 17. The period of rotation 


Figure 18. Mass 

Figure 19. 254 Low massstars in NGC 2516. The equatorial magnetic fields B (eq, Gauss) is plotted against the void radius 
Figure 20. The void radius Ro is plotted against the mass density D for the 254 stars in NGC 2516, represented by five averaged sets. Note that within this D range, when D increases Ro still increases with it, implying that gravity contraction has not been effective in these 254 stars. It is interesting to note that the power index is only 0.4123. We expect for Dwarfs, such an index in the

Figure 21. Employing values in Table 6, theoretically deduced equatorial dipolar magnetic field B (Gauss) against rotation period 
Table 6. Data of 1350 Brown dwarfs in the Pleiades [50] [51] [52] . The data of the last three brown dwarfs are taken from [36] . Parameters include mass M, radius R, period of rotation P, mass density D are entered into this table. Here, the radius is assumed to follow the Hamada-Salpeter model [41] for dwarfs. The intrinsic dipolar magnetic field along the equator 






Or

Since the graph of log P against log R is linear with a slope of +2.4462 (see Figure 22), Equation (6.6.3b) can be expressed as

under the constrain

Or

The log M versus log R plot in Figure 23 shows a slope of 1.185. The discrepancy is rather expected as the data points in the 


Figure 22. Each of the set of 9 data points labelled BDL in Table 6 represents the average of 150 stars. Using these data, together with other three members in the same table, (i.e., TVLM, J0036, J1835) the 



Figure 23. Using data in Table 6, we show the 
Figure 24. Surface equatorial field B (eq, theory, Gauss) vs the normalized void radius Ro/R for averages of 1353 Brown Dwarfs thin a rather wide range mass density as specified. This is an illustration of the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. The maximum value on the horizontal axis is 10−2. The slope is 3.0 as depicted in expression (4.2.14).
6.7. White Dwarfs
Basic data for a number of White Dwarfs are obtained from [53] [54] [55] . Other variables are calculated and entered into Table 7. Using sets of (B, P) values, we show in the usual way the B-P graph in Figure 25, finding the slope to be by

We have found that numerically, as in other star groups the LHS of the following equation is an approximate constant:

leading to

Equation (6.7.2b) indicates that our theory predicts a large negative slope
Table 7. White dwarfs. This table lists Mass









Figure 25. Employing values in Table 7, theoretically deduced surface equatorial dipolar magnetic field B (eq, theory, Gauss) against rotation period 


Figure 26. Refer to Table 7. The period of rotation 


Salpeter relation for dwarfs for decades [41] . It is difficult at this stage to obtain well defined power law relation for the P-R relation with sample masses within a narrow range of

In other words, expression (6.7.2b) becomes

For stars at younger age, fusion processes bring in heavier elements, but the density is low so that the gravitation contraction cannot overcome centrifugal force, and positive slopes should result in the P-R plots, as observed experimentally. More detailed discussion requires the analysis of the variation of mass density mathematically as a function of R.
Employing data values in Table 7, theoretically deduced equatorial dipolar magnetic field B (eq, theory, G) vs the void radius 


Figure 27.Employing data values in Table 7, theoretically deduced equatorial dipolar magnetic field B (Gauss) against the void radius 

now. Some detect field~Tesla or more, and some measurements lead to the suggestion that while there are two types of White Dwarfs-one with negligible magnetic field and another type with huge magnetic field. We have devoted one short section on the plausible origin of the sporadic fields, explained in terms of Chern-Simon potential in Secction (5) already. Equations 6.7.2(a) & 6.7.2 (c) might be considered to be the two laws consequential to the new Equation (6.7.1) for White Dwarfs of low masses as stated.
6.8. Magnetic White Dwarfs
Taking 7 Magnetic Whit Dwarf (MWD) samples [40] [55] [56] with close mass density values, we plot the B-P graph in Figure 28, using data in Table 8. Now the slope of Figure 28 is

Leading to;

The function C1 for the seven members are respectively 319.864, 318.5664, 319.917, 318.75, 319.635, 319.16, 319.40. The average K1 is about 319.33 (see Figure 29).
Therefore (6.8.2) becomes

Or

Now the relation between Mass and radius is assumed to follow the model of Hamada and Salpeter. Using data in Table 8, we show the M-R graph in Figure 30 giving a slope of −1.159. Substituting therefore the following equation

Figure 28. Employing values in Table 8, theoretically deduced equatorial dipolar magnetic field B (eq, theory, Gauss) against rotation period 
Figure 29. The values of the function C1 in Equation (6.8.2) are very close to a constant with a mean of 319.33 (SI units).
Table 8. Magnetic White Dwarfs. Parameters include mass M, radius R, period of rotation P, mass density D, the deduced void radius




Into Equation (6.8.3b), we arrive at

So far, we can consider that the theoretical Equation (6.8.1) leads to (6.8.5) using only the stated M-R relation, with input of “raw data”. When we plot 

We show the relation between the void radius 
Figure 30. Mass 

Figure 31. The relation between the void radius 

7. General Discussion and Summary
7.1. The Mystery of the Relationship between Surface Magnetic Field and Equatorial Rotational Speed of Stars
It is well known that the three groups of Zeeman components, 


On the other hand, measuring directly the features of Zeeman splitting in stellar spectral lines offers another method of detection of surface magnetic field strength of a star. However, such method, which in principle, should give more accurate surface magnetic fields, is limited to field strength greater than 





We have analyzed the B (equatorial, theory) ?P relation for 8 groups of stars in the last section. Experimentally, it has long been discovered that the mean projected rotational velocity 


Blackett found a positive correlation between the magnetic moment 















Now if the “magnetic Bode’s Law” is established, two important issues emerge: (i) Since an electric current or permanent magnet must exist to generate a magnetic field, it is of fundamental interest in physics to know how the Maxwell equations are “hidden behind”/within the magnetic Bode’s law; (ii) On the application side, variables in magnetism (magnetic field, flux) can be calculated from variables of mechanics (period of rotation, radius, mass) and vice versa if only one is unknown; (iii) Various models of dynamo theories have been proposed to explain the source of dipolar field and sporadic fields of stars. We note that long ago, using over ten thousand spot samples, it has been shown, using rather stringent statistics (the Maximum-likelihood analysis) that there is no statistical evidence that sunspots in the northern hemisphere and southern hemisphere are correlated [70] . This result supports the theory that the solar flare phenomenon is more likely to be associated with local variations.
In 1996, Baliunas, et al. reported the values of measured magnetic fields of 112 low main sequence stars (type F to late K with one M) [71] by analyzing features of the spectral lines arising from Zeeman splitting mentioned earlier, carried over 25 years at Mount Wilson Observatory. The rotation periods of 80 stars were inferred from periodic fluctuations with the stated Ca II records; for the other 32 stars, rotation was computed from the close relation between Ca II flux and the Rossby number (see details of Rossby number in [72] ) in order to reduce the errors due to the unknown values of the angle i between the magnetic axis of rotation and the line of sight. The authors employ a quantity RHK’ (called magnetic heating parameter) to approximate the magnetic moment µm and presented the 




It is therefore fruitful to compare our theoretical prediction with measured data within one main star type with more samples than in the last section.
Incidentally, more recently, Marsden et al. [74] compiled a rather comprehensive survey of the data of 170 sun-like stars, providing the measured “longitudinal surface magnetic field




7.2. Comparison between Theoretical Deduced Surface Magnetic Fields and Measured Values for Sun-Like Stars with Age Smaller Than about 3 Gyr
Since the magnetic field measured is the average surface “longitudinal” field, we use the polar magnetic field derived from our theory in Section (5), which is simply twice the equatorial field, and plot the dependent variable B (polar, theory, G) in Gauss against the measured 


One can use the “raw data” and plot the mass vs radius graph, for sun-like stars with density in the range 


In Figure 34, the theoretically derived polar magnetic field is plotted against the period of rotation 


Table 9. (a) Young Sun-like stars. Entry numbers in columns 1, 2, 3, 4, 5, 7 are taken directly from [74] and entries of other columns are deduced or calculated based on the present theory. When the age information is not available (N), raw data are still used if 





Figure 32. The surface dipole field at the pole vs the parameter


Figure 33. Putting the measured data based on Table 9(a) into Figure 32, we have Figure 33 above, showing that the experimental result (triangles; the deep/light blue ones pertain to the higher/lower density groups respective) and theoretical prediction (circles) are rather close in astronomical estimation. The power indices of the two straight lines are respectively 0.5506(deep reed) & 0.5563 (light red). The correlation coefficients are already specified in Figure 32.
Figure 34. The theoretically derived polar magnetic field vs the period of rotation 


the last section for other star groups. Putting the measured data listed in Table 9(a) into Figure 34, we arrive at Figure 35, and we observe that both the measured (triangles) and theoretical (circles) magnetic fields decrease with increasing P with the same general trend.
The only parameter value we have assumed, based on the argument explained twice before, is the Fermi energy of the spinor to be equal to the rest mass of electron. The cool stars considered in this sub-section and the next is similar to the regime of the Second Law of angular momentum we derived in [2] and this paper.
Now we proceed to analyze the relation between the magnetic parameter 





Figure 35. Putting the measured data as listed in Table 9(a) into Figure 34, we obtain the above graph, showing that both the measured (triangles; the deep/light blue ones pertain to the higher/lower density groups respective) and theoretical polar magnetic fields (circles) decrease with increasing P. The power indices of the two straight lines are respectively-0.741 (deep reed) &−0.716 (light red). The correlation coefficients are already specified in Figure 34.
Figure 36. The magnetic parameter

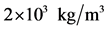


7.3. Comparison between Theoretical Deduced Surface Magnetic Fields and Measured Values for Old Sun-Like Stars with Age Greater Than about 3 Gyr
We will not take too much space to indicate all graphs above for the older sun- like stars, because there is high similarity in some. Based on data listed in Table 9(b), in Figure 37, we present the relevant graphs that are related to our discussion--Mass vs radius of sun-like stars with age between ~3 and 13 Gyr. The red triangles represent those with mass density between 1.0 to 2.5 times 

Figure 37. Mass vs radius of sun-like stars with age between ~3 and 13 Gyr. The red triangles represent those with mass density between 1.0 to 2.5 times 


The variation of the theoretical equatorial fields of old sun-like stars with changing P is demonstrated in Figure 38(a). The red circles represent those stars with mass density in the range 







Figure 38. (a) The theoretical equatorial fields of old sun-like stars change with variation of rotation period P. The red circles represent those stars with mass density in the range


Using raw data in [74] , the magnetic parameter 
7.4. Explanation of the Magnetic Bode’s Law and the Law of Intrinsic Dipolar Field for Stellar Objects
We have provided names “young” & “old” for sun-like stars. The separation is not arbitrary. If we go through the data in Table 9(a) and Table 9(b), we will notice that most of the young stars have masses and radii satisfying roughly




Now let us recollect that we have derived an explicit expression for the equatorial field, represented by

And the magnetic parameter is


Figure 39. The magnetic parameter 
Figure 40. The magnetic parameter 



where C1, C2 are constants. So our theoretical derivation tells us that if we plot 

Let us finally proceed to obtain demonstration of the Law of Intrinsic Dipolar Magnetic Field for Stellar Objects. When the equatorial field 

Figure 41. The theoretically deduced equatorial magnetic fields of sun-like stars with age > about 3 Gyr vs the normalized void radius



For comparison, the measured surface magnetic fields published in [74] are plotted against 
We have shown only samples of one star group as an illustration. Other measured data points of the young stars behave in the same way. This law has been applied to analyze all the 8 star groups in Sections (6) & (7). We shall not repeat to show such similar graphs for other star groups. The reader can test this law readily. Such results show that once the “mechanical” data set (M, R, P) is obtained, the magnetic field can be calculated, without the explicit use of the Maxwell equations. This law is in line with the Law specified in Equation (7.2b) and the linear relation of 


7.5. On Dipolar Magnetic Fields of the Solar Planets and the Planets of the Trappist-1 System
There are some mysteries in the properties of the magnetic fields of our planets. Before we analyze them, let us list the relevant data/variables in Table 10 based on data from [75] [76] [77] . We plot the 


The reported measured equatorial fields of 7 planets are indicated by the orange triangles. According to rotation periods and their distances from the sun, it appears that five pairs appear-(i) Mercury (









In our model, the conformal projection of 



Table 10. The solar system. Parameters include mass M, radius R, period of rotation P, mass density D and the deduced void radius 




Figure 42. Theoretical equatorial magnetic fields of the 9 planets, treating them as stars, are indicated by the deep green circles. Taking into the consideration of the planets being appearing as 5 pairs and theoretically from Perelman entropy mapping as discussed in Section (7.5), B (eq, theory, G)/5 for the 9 planets are represented by the bright green circles―the B-P plot shows good correlation with a power index of −0.871. The reported measured fields are represented by orange triangles, and appear to be much closer to the bright green circles.
energy and thus rest mass of hadrons are the protons (composed of (u, u, d) quarks) and neutrons (composed of (u, d, d) quarks), meaning that the Lorentz mass shell contains only u and d quarks of charges (2/3)e, and -(1.3)e. To create a proton (u, u, d) and a neutron (u, d, d) from P1, it requires 2 e massless spinors states, but just 1-e massless spinor state. When all the possible electron-proton pairs are created, the system can only generate neutrons, or the sets of (u, d, d) quarks. The quark mass for neutron is





We plot the average surface temperature against distance from the sun in log- log scale (Figure 43), showing a straight line with power index of −0.593. If the planets were “materials” thrown out from the sun whose age is 4.6 Gyr, the heat energy of the planets would have been dissipated as thermal radiation, and the slope would be much steeper. We speculate that the solar system evolved from a Perelman entropy mapping. The angular momenta of the planets and the sun
Figure 43. Average surface temperature 
contribute to the total angular momentum of the Milky Way during the initial epoch. The rotation rate could have been deduced from the temperature if one were to observe these objects passed through a wide temperature range. Now these objects are already in the “cool range”, i.e. under the Second Law regime. Due to different processes of evolution and the fact that these stellar objects have very small masses as compared to the sun, the cooling process is very effective (so that the core temperature of the sun is >> than of the planets), and the mass density is in general much larger than that of the sun for the inner two pairs of planets.
In deriving the angular momentum of the e-trinos states in [2] , the normalized void radius 


Thus, we consider that the generation of planets via the existence of the star sun is represented by the same group symmetry, and the 9 planets can be counted as 5 twins (with Pluto with its binary as a pair, but lying in the asteroid zone of the solar system). The arrangement of these planets shows Lie Group symmetry, due to SU(3) symmetry. There are two parity of choices in each element of the five (pairs) representation. In other words, there is a(p, n) duplet at the mass level, and the stellar object would split into two in view of, effectively, the SU(3) symmetry. Since the observed data suggests there are 5 pairs, similar to correct for spin multiplicity in a Fermi gas, the possible quantum states need to be divided by 5 when we do the averaging process for the loop current in calculating the dipole magnetic field. Thus we divide the dipole field strength by 5, and show the B-P graph in Figure 42 also (bright green circles). It is interesting to note that the measured values are then close to the theorized ones; the theoretical and measured values of the Earth overlap. Field of Mars is far off. We will provide an explanation of this abnormality below.
Let us first come back to the process of generation of mass in an individual planet, after splitting into pairs. Normally the ec current states of different energy E, and opposite charge and velocity signs, are statistically random, and therefore the parity bias in surface mass creation by P1, is not favored, but non-zero. If such abnormal distribution occurs, the equal number of states within each hemisphere can then be broken. Let us propose a simple scenario for P1 projection in Mars. Suppose the 2 e states came from Northern hemisphere, while the -e state, came from 1 loop in the Southern hemisphere. If that had happened, then the remaining e spinors in the north loop was less than the remaining -e spinors in the south. Such a repeated P1 projection, during Mars cooling (note that there are many volcanoes detected), will result in the magnetic field strength at the South Pole much greater than that at the North Pole [78] . For a similar reason but to a less degree in the stated parity bias property during the P1 projection, Venus could have a very weak magnetic field.
The dipolar planetary magnetic field shields the stellar particles radiation from impacting the planet’s surface without much energy lost; the magnetic field also serves to sustain the planetary atmosphere and to reduce possible material ejection from the planet’s surface. Thus Mars with an uneven dipole field and a thin atmosphere is known to have sent rocks that hit the earth.
In passing, we would remark that projection Po of the in-phase spinor states on the 3D surface of the void generate electrons in the Lorentz manifold, but leaving behind net positive massless spinor states on the void surface. A net current resulting from such states would generate magnetic field. Similarly, projection P1 of the out- of-phase spinor states in the 1D loops of the void generate quarks in the Lorentz manifold, but leaving behind net negative massless spinor states in the current loops of the void surface. Both events would lead to variation of the surface magnetic fields. Whether this model could explain the reversal of dipole polarity is outside the scope of this paper. We would also emphasize that most quarks and electrons were created when Perelman mappings were being implemented. The number of in-phase and anti-phase spinor states left over within the 
According to [79] , the basic data sets of the six planets nearest to the newly discovered Trappist-1 system are
where 

7.6. Summary of the Discoveries Reported in This Paper
We have sketched the steps that during the mapping from 5D to 4D manifold, the 4th spatial variable in the 5D space-time structure would become the (non- zero) current loop with radius x’ at the 5D-4D boundary (one around each magnetic pole). In the unified 5D theories of Kaluza-Klein and Einstein, this space variable is compacted to zero, leading to gravitational singularity and hence black holes. Our deduction shows that such gravitational singularity does not exist, and the conclusion is well sup-
Figure 44. The theoretical equatorial dipole magnetic field of the six planets nearest to the newly discovered Trappist-1 system against the period of rotation
Figure 45. Change of 
ported by the numerous detections of stars with masses > 100 M⊙ (the largest one reported so far has a mass of
Comparing the time intervals after the Big Bang when the lightest lepton (electron) is generated and that when the three quarks (building up a proton) join to form a proton, we obtain the radius of the loop current x’ in terms of the void radius Ro:

for all stellar objects with hydrogen as fuel. The modification on x’ when the next heavier element (Helium) becomes the fuel of the star is also derived.
Analyzing the early stage of formation of a galaxy based on the 5D projection theory, we have provided an answer to the detection of unexpected gamma ray bubbles, one above, and one below a galaxy.
Since Maxwell equations are classical and valid in both the 5D and 4D manifolds, we have derived an explicit expression of the number density of the spinor pairs (which satisfies the Fermi-Dirac distribution but also form the current loop with radius x’ in the classical sense) at the 4D-5D boundary, with quantum signature based on (i) the uncertainty principle & (ii) quantum statistics. Viewed in a 4D Lorentz manifold, this current loop must produce a magnetic field in the classical sense. Therefore we simply apply the Biot-Savart law, with quantum nature incorporated in the number density of the e-trinos, to derive the expression of a distant magnetic field as observed on the matter surface of a stellar object. The surface magnetic field is found to be

The variables are only M, R, P as the Fermi energy 
Expanding 
as convergent series, we discover that the approximate expression for B can be separated into three regions in temperature domain. In the high temperature domain where

We call Equation (7.6.3) the Law of Intrinsic Dipole Magnetic Field for Hot Stars. This law is applicable to fast rotating pulsars at very high temperature.
On the other hand, if

Thus under the low temperature domain, B is independent of T. We call Equation (7.6.4) as the Law of Intrinsic Dipole Magnetic Field for Cool Stellar Objects. Such an interesting result is obvious because the angular momentum of the object is a function of the void radius Ro and the amount of current generated (hence the dipole field strength) near the magnetic poles in the 4D-5D boundary is also a function of Ro. The current density, which usually appears in Maxwell equations, is illuminated, giving the “un-ex- pected result” as specified in Equation (7.6.4). The transition temperature between the two domains is
Taking a cool star as a solid sphere as an approximation, it is elementary to show from Equation (7.6.4) that

which is simply the “mysterious Magnetic Bode’s Law” found experimentally for cool stars.
We have found that for samples within a range of mass density, the 
Moreover, based on the numerical analysis in Sections (6) & (7) for nine star groups, we have found that once the power index of the 
We have proposed that electrons of the elements (atoms), starting with hydrogen could form 2D Semion states, with pinning of magnetic flux. Due to pressure wave or, in fact fluctuations during the natural cooling process, Semion state can be formed on/near the stellar surface when the gravitational force is
Figure 46. Predicted equatorial magnetic fields against period of rotation P for the following star groups: (1) Pre-main sequences stars of the Orion (light purple); (2) NGC 6819(orange); (3) Low-to Mid-Mass main sequence stars (bright red); (4) Sun-like young stars (red slightly deeper than that of group (3)) & sun-like old stars (deep red). Notice that the young ones are close to groups (2) & (3), whereas the old ones are close group (1) instead.(5) Pre-dwarfs M34 (bright green); (6) NGC 2516 (pink); (7) Brown Dwarfs (brown); (8) White Dwarfs (blue); (9) Magnetic White Dwarfs (light bright blue). Note that the line of best fit is drawn through each group except the sun-like group (4). Since each group covers a relatively wide mass density, the slopes of the 8 lines above are slightly different from the values analyzed in Section (6). Many points of stars are overlapping. As data for some stars are averaged over a much larger number of stars, the total effective number of stars analyzed is well over 2000. Power indices and correlation coefficients have already been specified in the analysis of each star group.
very large and the void radius 
We have provided an explanation of the asymmetry of magnetic field on the Martian surface and compared the measured and theoretically deduced dipolar magnetic fields of the planets. For the different star groups we studied in Section (6), we cannot compare directly the theoretical magnetic field values with all the stars because we it is difficult to find the published complete set of data for most of these stars. Group comparison (such as Brown Dwarfs group) indicates that our predicted results are in line, in fact, within the same order of magnitude, with observational data and in general trends. For the sun-like group where the whole set of data (B, M, R, P) are available, theoretical predicted values agrees quite well with data (within an order of magnitude), considering the uncertainty and limitation in measurements discussed in details in Section (7.1).
We predict the equatorial fields B of the newly discovered Trappist-1 star and the 6 nearest planets. The B − P graph, and the B R3 ? Iω graph in the log-log plots for the 6 planets are both linear.
7.7. Conclusion
Based on the homogeneous 5D model of the universe, we have developed explicit expressions to explain quite a number of unanswered queries or mysteries in astrophysics, as outlined in Section (7.6). One step further, we hope that similar study can serve someway in building a part of the bridge to embrace Maxwell electro-magnetism and quantum mechanics in the future.
Acknowledgements
We wish to express our gratitude to the various types of assistance of Mr. Benjamin Fung and Dr. Junling Gao, Mr. Vincent Wan during the preparation of this manuscript. We appreciate Mr. Cressidy Fan for plotting Figure 1. We would also wish to express our thanks to Dr. Gisela Dreschhoff, and Dr. Hogne Jungner for their critically reading of the manuscript, plus Dr. Wilson Wong for discussion on issues related to this paper. Last but not least, we thank Professor W. K. Chow for his help when in need for this long project. Both authors declare that there is no conflict of interests in this academic project.
Cite this paper
Fung, P.C.W. and Wong, K.W. (2017) Origin of Magnetic Fields of Stellar Objects in the Universe Based on the 5D Projection Theory. Journal of Modern Physics, 8, 668-746. https://doi.org/10.4236/jmp.2017.84045
References
- 1. Wong, K.W., Dreschhoff, G.A.M. and Jungner, H. (2014) The Five Dimension Space-Time Universe—A Creation and Grand Unified Field Theory Model. Scientific Research Publishing, USA.
- 2. Fung, P.C.W. and Wong, K.W. (2015) Journal of Modern Physics, 6, 2303-2341.
https://doi.org/10.4236/jmp.2015.615235 - 3. Einstein, A. (1916) Die Grunlagen der allgemeinen relativitatstheorie. Annalen der Physik, 354, 769-822.
https://doi.org/10.1002/andp.19163540702 - 4. Schwarz, A.J. and Doughty, N.A. (1992) American Journal of Physics, 60, 150-157.
https://doi.org/10.1119/1.16935 - 5. Aczel, A.D. (1997) Fermat's Last Theorem: Unlocking the Secret of an Ancient Mathematical Problem. Penguin, London, 147 p.
- 6. Hainich, R., Rühling, U., Todt, H., Oskinova, L.M., Liermann, A., Gräfener, G., Foellmi, C., Schnurr, O. and Hamann, W.R. (2014) Astronomy and Astrophysics, 565, A27. arXiv:1401.5474
https://doi.org/10.1051/0004-6361/201322696 - 7. Bestenlehner, J.M., Gräfener, G., Vink, J.S., Najarro, F., De Koter, A., Sana, H., Evans, C.J., Crowther, P.A., Hénault-Brunet, V., Herrero, A., Langer, N., Schneider, F.R.N., Simón-Díaz, S., Taylor, W.D. and Walborn, N.R. (2014) Astronomy and Astrophysics, 570, A38. arXiv:1407.1837
https://doi.org/10.1051/0004-6361/201423643 - 8. Crowther, P.A., Caballero-Nieves, S.M., Bostroem, K.A., Maíz Apellániz, J., Schneider, F.R.N., Walborn, N.R., Angus, C.R., Brott, I., Bonanos, A., De Koter, A., De Mink, S.E., Evans, C.J., Gräfener, G., Herrero, A., Howarth, I.D., Langer, N., Lennon, D.J., Puls, J., Sana, H. and Vink, J.S. (2016) Monthly Notices of the Royal Astronomical Society, 458, 624-659. arXiv:1603.04994.
- 9. Arge, C.N. and Mullan, D.J. (1995) The Astrophysial Journal, 443, 795-803.
https://doi.org/10.1086/175569 - 10. Perelmann, G. (2003) Ricci Flow with Surgery on Three-Manifolds.
arXiv:math.DG/0303109 - 11. Perelmann, G. (2003) Finite Extinction Time for the Solutions to the Ricci Flow on Certain Three-Manifolds. arXiv:math/0307245
- 12. Perelmann, G. (2002) The Entropy Formula for the Ricci Flow and Its Geometric Applications. arXiv:math/0211159
- 13. Cao, H.-D. and Zhu, X.-P. (2006) Asian Journal of Mathematics, 10, 165-492.
https://doi.org/10.4310/AJM.2006.v10.n2.a2 - 14. Wong, K.W., Dreschhoff, G.A.M. and Jungner, H. (2015) Journal of Modern Physics, 6, 890-901.
https://doi.org/10.4236/jmp.2015.67093 - 15. Leonhard, E. (1770) Vollständige Anleitung zur Algebra. Royal Academy of Sciences, St. Petersburg.
- 16. Dickson, L.E. (2013) History of the Theory of Numbers: Diophantine Analysis, Dover Publication Inc., Mineola, New York, 832 p.
- 17. Nyambuya, G.G. (2016) Advances in Pure Mathematics, 6, 1-6.
- 18. Lindner, N.H., Peres, A. and Terno, D.R. (2003) Journal of Physics A: Mathematical & General, 36, 1-4.
https://doi.org/10.1088/0305-4470/36/29/101 - 19. NASA (2010) Fermi Discovers Giant Gamma-Ray Bubbles in the Milky Way.
http://svs.gsfc.nasa.gov/goto?10688 - 20. Lee, T.D. and Yang, C.N. (1956) Physical Review, 104, 254.
https://doi.org/10.1103/PhysRev.104.254 - 21. Warnick, K.F. and Russer, P. (2006) Turkish Journal of Electrical Engineering and Computer Sciences, 14, 153-171.
- 22. Maxwell, J.C. (1864) A Dynamical Theory of the Electromagnetic Field. The Royal Society Transactions, Volume CLV. Printed in: The Scientific Papers of James Clerk Maxwell (W.D. Niven), Two Volumes Bound as One, Volume One, New York, Dover Publications, Inc., 1890, 526.
- 23. Silagadze, Z.K. (2002) Feynman’s Derivation of Maxwell Equations and Extra Dimensions. arXiv:hep-ph/0106235v2
- 24. Wong, K.W., Dreschhoff, G.A.M. and Jungner, H. (2015) Journal of Modern Physics, 6, 890-901.
https://doi.org/10.4236/jmp.2015.67093 - 25. Wheeler, J.A. (1955) Physical Review Online Archive (Prola), 97, 511-536.
Wheeler, J. (1957) Annals of Physics, 2, 604-614. - 26. Azzurli, F. and Lechner, K. (2014) Electromagnetic Fields and Potentials Generated by Massless Charged Particles. arXiv:1401.5721v1
- 27. Hawking, S. and Mlodinow, L. (2010) The Grand Design. Bantam Books, New York.
- 28. Witze, A. (2012) Science News, 182, 5-6.
https://doi.org/10.1002/scin.5591820203 - 29. Wong, K.W., Dreschhoff, G. and Jungner, H. (2012) Journal of Modern Physics, 3, 1450-1457.
https://doi.org/10.4236/jmp.2012.310179 - 30. Edwin Cartlidge. News-Science and Environment: Galactic X-Rays Could Point to Dark Matter Proof.
http://www.bbc.com/news/science-environment-38841577 - 31. Dunne, G.V. (1999) Aspects of Chern-Simons Theory. arXiv:hep-th/9902115v1
- 32. Moore, J.E. (2014) Physics 250 Fall: Set 4 of Lecture Notes, UC Berkeley and LBNL (Dated: October 13, 2014): B. Chern-Simons Theory II: Integrating out Gauge Fields and Coupling to Electromagnetism.
- 33. von Steinkirch, M. (2010) Maxwell-Chern-Simons Theory.
http://astro.sunysb.edu/steinkirch/reviews/CHERNSIMONS.pdf
Caruso, F., Helayël-Neto, J.A., Martins, J. and Oguri, V. (2012) Effects on the Non-Relativistic Dynamics of a Charged Particle Interacting with a Chern-Simons Potential. arXiv:1211.5597v2 - 34. Yang, X.L., Guo, S.H., Chan, F.T., Wong, K.W. and Ching, W.Y. (1991) Physical Review A, 43, 1186.
https://doi.org/10.1103/PhysRevA.43.1186 - 35. Gou, S.H., Yang, X.L., Chan, F.T., Wong, K.W. and Ching, W.Y. (1991) Physical Review A, 43, 1197.
https://doi.org/10.1103/PhysRevA.43.1197 - 36. Dreschhoff, G., Jungner, H., Wong, K.W. and Perry, C.A. (2015) Journal of Modern Physics, 6, 1095-1103.
https://doi.org/10.4236/jmp.2015.68114 - 37. Hallinan, G., Antonova, A., Doyle, J.G., Bourke, S., Lane, C. and Golden, A (2008) The Astrophysical Journal, 684. arXiv:0805.4010v1
https://doi.org/10.1086/590360 - 38. Fung, P.C.W. (1969) Canadian Journal of Physics, 47, 179-194.
https://doi.org/10.1139/p69-021 - 39. Fung, P.C.W. (1969) Canadian Journal of Physics, 47, 161-177.
https://doi.org/10.1139/p69-020 - 40. Brinkworth, C.S., Burleigh, M.R., Lawrie, K., Marsh, T.R. and Knigge, C. (2013) The Astrophysical Journal, 773, 47.
- 41. Hamada, T. and Salpeter, E.E. (1961) The Astrophysical Journal, 134, 683-697.
https://doi.org/10.1086/147195 - 42. Stassun, K.G., Mathieu, R.D., Mazeh, T. and Vrba, F.J. (1999) The Astrophysical Journal, 117, 2941-2979.
https://doi.org/10.1086/300881 - 43. Meibom, S., Bames, S.A., Platais, I., Gilliland, R.L., Latham, D.W., Mathieu, R.D. (2015) Nature, 517, 589-591.
https://doi.org/10.1038/nature14118 - 44. Demircan, O. and Kahraman, G. (1991) Astrophysics and Space Science, 181, 313-322.
https://doi.org/10.1007/BF00639097 - 45. Feiden, A. and Chaboyer, B. (2012) The Astrophysical Journal, 757, 42.
- 46. McQuillan, A. and Mazeh, T. (2014) Astrophysics Journal Supplement Series, 24, 14 p. (Also see NASA FACT SHEET-main sequence stars)
- 47. Irwin, J., Aigrain, S., Hodgkin, S., Irwin, M., Bouvier, J., Clarke, C., Hebb, L. and Moraux, E. (2006) Monthly Notices of the Royal Astronomical Society, 370, 954-974.
https://doi.org/10.1111/j.1365-2966.2006.10521.x - 48. Ventrudo, B. (2009) ESA’s the Southern Beehive Cluster.
http://americaspace.com/ - 49. Irwin, J., Hodgkin, S., Aigrain, S., Hebb, L, Bouvier, J., Clarke, C., Moraux, E. and Bramich, D.M. (2007) Monthly Notices of the Royal Astronomical Society, 377, 741-758.
https://doi.org/10.1111/j.1365-2966.2007.11640.x - 50. Scholz, A. and Eisloffel, J. (2004) Astronomy & Astrophysics, 421, 259-271.
https://doi.org/10.1051/0004-6361:20035857 - 51. McQuillan, A., Aigrain, S. and Mazeh, T. (2013) Monthly Notices of the Royal Astronomical Society, 432, 1203-1216.
https://doi.org/10.1093/mnras/stt536 - 52. Martin, E.L. and Zapatero-Osorio, M.R. (1997) Monthly Notices of the Royal Astronomical Society, 286, L17-L20.
https://doi.org/10.1093/mnras/286.1.L17 - 53. Kawaler, S.D. (2003) White Dwarf Rotation: Observations and Theory. Stellar Rotation. Proceedings IAU Symposium No. 215, @ 2003 IAU, Andre Maeder & Philippe Eenens, Eds.
- 54. Provencal, J.L., Shipman, H.L., Hog, E. and Thejll, P. (1998) The Astrophysical Journal, 494, 759-767.
https://doi.org/10.1086/305238 - 55. Johnson, J. (2007) Extreme Stars: White Dwarfs & Neutron Stars. Lecture Notes, Astronomy 162, Ohio State University, Columbus, OH.
- 56. Bagnulo, S., Monin, D., Fabrika, S., Lee, B.C., Galazutdinov, G., Wade, G.A. and Burlakova, T. (2005) Astronomy & Astrophysics, 439, 1099-1106.
https://doi.org/10.1051/0004-6361:20052642 - 57. Chin, Y.C., Lusignan, B.B. and Fung, P.C.W. (1971) Solar Physics, 16, 135-151.
https://doi.org/10.1007/BF00154509 - 58. Tinbergen, J. (1996) Astronomical Polarimetry. Cambridge University Press, Cambridge, New York.
- 59. Borra, E.F. and Deschatelets, D. (2015) The Astronomical Journal, 150, 146.
arXiv:1509.04544 - 60. Cheng, F.T. and Fung, P.C.W. (1977) Astrophysics and Space Science, 49, 427-442.
https://doi.org/10.1007/BF00641990 - 61. Fung, P.C.W. and Cheng, F.T. (1977) Astrophysics and Space Science, 52, 243-264.
https://doi.org/10.1007/BF01093866 - 62. Cheng, F.T. and Fung, P.C.W. (1979) Astrophysics and Space Science, 63, 177-183.
https://doi.org/10.1007/BF00647754 - 63. Bailey, J.D. (2014) Astronomy &Astrophysics, 568, 1-6.
- 64. Fung, P.C.W. and Yip, W.K. (1966) Australian Journal of Physics, 19, 759-794.
https://doi.org/10.1071/PH660759 - 65. Fung, P.C.W. (1966) Planetary and Space Science, 14, 469-481.
- 66. Abt, H.A., Clement, A.E., Doose, L.R. and Harris, D.H. (1969) The Astronomical Journal, 74, 1153-1154.
https://doi.org/10.1086/110916 - 67. Reiners, A. (2012) Living Reviews in Solar Physics, 9, 1.
- 68. Blackett, P.M.S. (1947) Nature, 159, 658-666.
Hales, A.L. and Gough, D.I. (1947) Nature, 160, 746. - 69. Russell, C.T. (1978) Nature, 272, 147-148.
https://doi.org/10.1038/272147a0 - 70. Fung, P.C.W., Sturrock, P.A., Switzer, P. and Hover, G.V. (1971) Solar Physics, 18, 90-99.
https://doi.org/10.1007/BF00146037 - 71. Baliunas, S., Sokoloff, D. and Soon, W. (1996) The Astrophysical Journal Letters, 457, L99-L102.
- 72. Noyes, R.W., Hartman, L.W., Baliunus, S.L., Duncan, D.K. and Vaughan, A.H. (1984) The Astrophysical Journal, 279, 763-777.
- 73. Montesinos, B. and Jordan, C. (1993) Monthly Notices of the Royal Astronomical Society, 264, 900-918.
https://doi.org/10.1093/mnras/264.4.900 - 74. Marsden, S.C., Petit, P., Jeffers, S.V., Morin, J., Fares, R., Reiners, A., do Nascimento Jr., J.-D., Auriere, M., Bouvier, J., Carter, B.D., Catala, C., Dintrans, B., Donati, J.-F., Gastine, T., Jardine, M., Konstantinova-Antova, R., Lanoux, J., Lignieres, F., Morgenthaler, A., Ramirez-Velez, J.C., Theado, S., Van Grootel, V. and The BCool Collaboration (2014) Monthly Notices of the Royal Astronomical Society, 444, 3517-3536.
https://doi.org/10.1093/mnras/stu1663 - 75. Williams, D.R. (2013) Sun Fact Sheet. NASA.
- 76. Williams, D.R. (2015) NASA “Planetary Fact Sheets”. dave.williams@nasa.gov
- 77. Tony Phillips (2008-07-03) New Discoveries at Mercury. Science@Nasa. Retrieved 2011-07-16.
- 78. Emily Lakdawalla. Why Is Only Half of Mars Magnetized? 2008-10-24.
http://www.planetary.org/blogs/emily-lakdawalla/2008/1710.html - 79. Trappist-1.
http://pixsosi.com/index.php/2017/02/22/seven-earth-like-planets-discovered-about-single-star/
Appendix A: Explicit Expression of the Void Radius
To calculate the void radius

where


If we treat s pair of in-phase spinors of opposite charge as a bound state, the energy is taken to be the additive energy in the pair. We have already noted in [6] that e,-e are two different types of Fermi particles, and the total angular momentum is then twice of that pertains to either one type―the above expression is then multiplied by a factor of two. The resulting total angular momentum deduced from these two types of treatment different by a numerical constant of several times only. For astronomical estimation, we have considered the loop current based on the Biot-Savart Law to be the additive sum of two currents due to oppositely rotating spinor charges in section (4). Here we also take that the total angular momentum of the system to be twice that in the above equation. Integrating over

The constant D is found to be:

Under the region satisfied by the Second Law of Angular Momentum, it has been shown in [2] that

Considering a stellar object to be a solid sphere with mass M, radius R, period of rotation P, conservation of angular momentum among the 5D void and the 4D matter shell requires that
Giving

Numerically,

The dimension of

Appendix B: Converging Series of the Integral

where


With


is bounded for a wide range of 


Now 
Integration by parts gives,






Summing all the series, we arrive at

Transforming

From (B.1), (B.12),(B.13),

When

When

Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact jmp@scirp.org




































































