Journal of Modern Physics
Vol. 2 No. 7 (2011) , Article ID: 5838 , 7 pages DOI:10.4236/jmp.2011.27087
Calculation of the Zeeman-Fine Energies and the Spectrum with Doppler-Shift Correction of Atomic Lithium
Department of Physics and Astronomy, King Saud University, Riyadh, Saudi Arabia
E-mail: {lbabsail, leda, salwam, smasuda}@ksu.edu.sa
Energies, Photonic Transitions, Quantum Flux of Photon
Received April 18, 2011; revised May 27, 2011; accepted June 12, 2011
Keywords: Hydrogen-Like Atoms, Effective Landé G-Factor, Quantum Entanglement, Zeeman-Fine
ABSTRACT
We have calculated the Zeeman-fine energies of atomic Lithium (Li) by using the varying effective Landé g-factor method. We take the principle quantum number in the range; (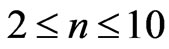 ). For this range we find 26 different energy values and 325 wavelengths some of which are the same. The Doppler shift is found to be
). For this range we find 26 different energy values and 325 wavelengths some of which are the same. The Doppler shift is found to be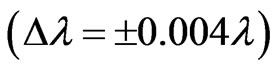 . The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li.
. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li.
1. Introduction
The investigation of hydrogen-like atoms with their low ionization potential and relative simplicity of their outer shell structure, have attracted a lot of attention. During the last two decades with the advent of laser cooling [1-4] and magnetic trapping [5], as well as spin polarization related to quantum entanglement [6], lithium and sodium have been the focus of a number of theoretical and experimental studies. Moreover with the realization of Bose Einstein condensation [7,8], they have attracted further attention.
Recently Saglam et al. [9] calculated the Zeeman-fine energy expression of hydrogen-like atoms given by:

corresponding to the eigenstates . Here the constant
. Here the constant  is a characteristic for each atom and determined from the ionization energy,
is a characteristic for each atom and determined from the ionization energy,  is the cyclotron angular frequency corresponding to the effective magnetic field,
is the cyclotron angular frequency corresponding to the effective magnetic field,  inside the atom and
inside the atom and  is the effective Landé g-factor, which is treated as a varying parameter. As was discussed by Saglam et al. [9] the effective magnetic field,
is the effective Landé g-factor, which is treated as a varying parameter. As was discussed by Saglam et al. [9] the effective magnetic field,  can be very high so that this leads to the spin-flip energies of the order of (eV). For the case of atomic Cesium, the spin-flip energy was shown to be 1.38 eV. Saglam et al. [9] defined a dimensionless function:
can be very high so that this leads to the spin-flip energies of the order of (eV). For the case of atomic Cesium, the spin-flip energy was shown to be 1.38 eV. Saglam et al. [9] defined a dimensionless function:

which takes the form:

and depends on  and
and  directly and depends on
directly and depends on  indirectly as the range of
indirectly as the range of  is determined by
is determined by . They used the plots of
. They used the plots of
 (as a function of
(as a function of ) to study the
) to study the
( )
)  (
( )
) (
( )
)
transitions in hydrogen-like atoms and showed that the entanglements of  and
and  states, occur at
states, occur at . The aim of the present study is to calculate the Zeeman-fine energies and the spectrum of the atomic Lithium by using the above mentioned varying effective Landé g-factor method. The outline of the present study is as follows: In Section 2.1 the energy levels of Hydrogen-like atoms in the presence of a uniform magnetic field is studied. In Section 2.2 we calculate the Zeeman-fine energies of Li atom. In Section 2.3 we establish the connection between the Zeeman-fine energies, effective Landé-g factors, and the quantum flux of both photon and the electronic orbits corresponding to the entangled states. Section 2.4 gives the detailed calculation of the Zeeman-fine energies of Li atom. The calculation of the Doppler shift is given in Section 2.5. Section 3 is the conclusions.
. The aim of the present study is to calculate the Zeeman-fine energies and the spectrum of the atomic Lithium by using the above mentioned varying effective Landé g-factor method. The outline of the present study is as follows: In Section 2.1 the energy levels of Hydrogen-like atoms in the presence of a uniform magnetic field is studied. In Section 2.2 we calculate the Zeeman-fine energies of Li atom. In Section 2.3 we establish the connection between the Zeeman-fine energies, effective Landé-g factors, and the quantum flux of both photon and the electronic orbits corresponding to the entangled states. Section 2.4 gives the detailed calculation of the Zeeman-fine energies of Li atom. The calculation of the Doppler shift is given in Section 2.5. Section 3 is the conclusions.
2. Formalism
2.1. Energy Levels of Hydrogen-Like Atoms in the Presence of a Uniform Magnetic Field
As was discussed by Saglam et al. [9], when an atom is subject to a laser beam, because of the photon’s magnetic moment [10] and hence the large intrinsic magnetic field along the propagation direction [11], we will have diamagnetic and paramagnetic effects which is associated with a large magnetic field inside the atom. This field is called the effective field, . The Landé-g factor is also replaced by the effective value,
. The Landé-g factor is also replaced by the effective value,  which is treated as a varying parameter [12,13]. With these replacements [9] the energy eigenvalues corresponding to the eigenstates
which is treated as a varying parameter [12,13]. With these replacements [9] the energy eigenvalues corresponding to the eigenstates  reads:
reads:
 (1)
(1)
Here the constant  is the characteristic of each atom and determined from the ionization energy. Substituting the value of
is the characteristic of each atom and determined from the ionization energy. Substituting the value of  and
and  in Equation (1), we find:
in Equation (1), we find:
 (2)
(2)
where  is the cyclotron angular frequency corresponding to
is the cyclotron angular frequency corresponding to . As was discussed by Saglam et al. [9] the effective magnetic field,
. As was discussed by Saglam et al. [9] the effective magnetic field,  inside the atom can be very high so that this leads to the spin flip energies at the order of a few electron volts (eV). For the case of atomic Cesium, the spin flip energy is taken to be 1.38 eV. To proceed further, following Saglam et al. [9] we define a dimensionless function,
inside the atom can be very high so that this leads to the spin flip energies at the order of a few electron volts (eV). For the case of atomic Cesium, the spin flip energy is taken to be 1.38 eV. To proceed further, following Saglam et al. [9] we define a dimensionless function,  which is given by the relation:
which is given by the relation:
 (3a)
(3a)
or
 (3b)
(3b)
which depends on  and
and  directly and depends on
directly and depends on  indirectly as the range of
indirectly as the range of  is determined by
is determined by . The plot of these
. The plot of these  functions with respect to
functions with respect to  gives us the possible
gives us the possible  values in the energy expression given by (1). At the first glance we see that the crossing of these lines correspond to integer values of
values in the energy expression given by (1). At the first glance we see that the crossing of these lines correspond to integer values of  such as:
such as: . However in the following section we will see that for Li atom the allowed values of
. However in the following section we will see that for Li atom the allowed values of  are restricted only with the three odd integers. These are:
are restricted only with the three odd integers. These are: . In the present study we will consider only
. In the present study we will consider only  values up to 10. We will see that in the range of (
values up to 10. We will see that in the range of ( ) we get 26 different energy values which produce 325 wavelengths some of which are the same. For each
) we get 26 different energy values which produce 325 wavelengths some of which are the same. For each  value we also calculate the Doppler shift and find that it is equal to:
value we also calculate the Doppler shift and find that it is equal to:  . The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values [14] for atomic Li.
. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values [14] for atomic Li.
2.2. Calculation of the Effective Landé G-Factors of the Zeeman-Fine Energies of Li Atom
In Li atom we have 3 electrons altogether. Therefore it will be easy to study  as a function of
as a function of . The plots for
. The plots for  and
and  are given in Figures 1(a) and 2(a) respectively; For
are given in Figures 1(a) and 2(a) respectively; For  we have
we have  and hence
and hence , so from Equation (3) we get two lines crossing at
, so from Equation (3) we get two lines crossing at . Therefore the first two electrons occupy the entangled state, with the energy corresponding to the crossing energies of
. Therefore the first two electrons occupy the entangled state, with the energy corresponding to the crossing energies of  and
and  states, which is the
states, which is the entanglement at
entanglement at  (Figure 1(a)). For
(Figure 1(a)). For  we have
we have  and hence
and hence , so from Equation (3), the plots of
, so from Equation (3), the plots of  gives us the diamond shaped parallelogram whose corners correspond to
gives us the diamond shaped parallelogram whose corners correspond to  entanglement at
entanglement at ,
,  and
and  entanglements at
entanglements at  and
and  entanglement at
entanglement at  (Figure 2(a)). Therefore the third electron (the so called 2s electron) occupies the entangled state at crossing of
(Figure 2(a)). Therefore the third electron (the so called 2s electron) occupies the entangled state at crossing of  and
and  states [(
states [( ) entanglements at
) entanglements at ] which corresponds to the lowest energy, the ground state energy, for
] which corresponds to the lowest energy, the ground state energy, for . The plots of energy expression (2) for
. The plots of energy expression (2) for  and
and  are given in Figures 1(b) and 2(b) respectively. In order to find the excited states we go to the higher values of
are given in Figures 1(b) and 2(b) respectively. In order to find the excited states we go to the higher values of . The plots of
. The plots of  and
and for
for  and
and  are given in Figures 3 and 4 respectively. We see that although the crossings of these lines occur at the integer values of
are given in Figures 3 and 4 respectively. We see that although the crossings of these lines occur at the integer values of  such as:
such as: , however, as far as the photonic transitions are concerned, in the following section we will see that for Li atom the allowed values of
, however, as far as the photonic transitions are concerned, in the following section we will see that for Li atom the allowed values of  are restricted only with the three odd integers. These are:
are restricted only with the three odd integers. These are: . The reason for this is that: First, The energy values given by (2) are limited to the range:
. The reason for this is that: First, The energy values given by (2) are limited to the range: . Secondly, the value of the spin-flip energy which is equal to
. Secondly, the value of the spin-flip energy which is equal to  for Li atom and finally, the photonic transitions occur between the points satisfying the condition: (
for Li atom and finally, the photonic transitions occur between the points satisfying the condition: ( even integer). In passing we note that for a given
even integer). In passing we note that for a given , although the maximum value of
, although the maximum value of  is equal to (
is equal to ( ), any energy value corresponding to
), any energy value corresponding to  can be obtained by the values in the range:
can be obtained by the values in the range:  as well.
as well.
Therefore the  values in this reduced zone (
values in this reduced zone ( ) will give us all the possible energy values.
) will give us all the possible energy values.
 (a)
(a) (b)
(b)
Figure 1. (a)  as a function
as a function ; (b)
; (b)  as a function of
as a function of 
2.3. Flux Quantization Argument
Let us assume that the ground state electron [the electron occupying the ( ) entangled state at
) entangled state at ] is excited to a higher level by the absorption of a single photon. Now we ask: What is quantum flux difference between the final and initial states? Recently Saglam and Sahin [10,11] showed that, depending on its helicity photon carries an intrinsic magnetic moment and hence a quantum flux of
] is excited to a higher level by the absorption of a single photon. Now we ask: What is quantum flux difference between the final and initial states? Recently Saglam and Sahin [10,11] showed that, depending on its helicity photon carries an intrinsic magnetic moment and hence a quantum flux of  where
where  is the flux quantum. Therefore in the end of a one photon absorption process the quantum flux difference between the final and initial quantum states of electron must be equal to the intrinsic quantum flux of the absorbed photon which is equal to
is the flux quantum. Therefore in the end of a one photon absorption process the quantum flux difference between the final and initial quantum states of electron must be equal to the intrinsic quantum flux of the absorbed photon which is equal to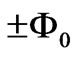 . On the other hand Saglam et al. [15]
. On the other hand Saglam et al. [15]
 (a)
(a) (b)
(b)
Figure 2. (a)  as a fuction of
as a fuction of ; (b)
; (b)  as a function
as a function .
.
also calculated the quantized magnetic flux through the electronic orbits of Dirac hydrogen atom corresponding to the . It is shown that the quantum flux is given by:
. It is shown that the quantum flux is given by: . For the present case we have the entangled states with the energies given by (1) where we have (
. For the present case we have the entangled states with the energies given by (1) where we have ( ) which stands for
) which stands for . Therefore for the present case the quantum flux through the orbits corresponding to the entangled states in hydrogen-like atoms will be given by:
. Therefore for the present case the quantum flux through the orbits corresponding to the entangled states in hydrogen-like atoms will be given by:
 (4)
(4)
We have stated that when the ground state electron is
 (a)
(a) (b)
(b)
Figure 3. (a)  as a function
as a function ; (b)
; (b)  as a function
as a function .
.
excited to a higher level with an absorption of one photon (or more photons) the flux difference between two quantum orbits must be equal to integer multiples of ( ). Therefore the difference of the flux in (4) must be equal to integer multiples of (
). Therefore the difference of the flux in (4) must be equal to integer multiples of ( ). In (4), since we have
). In (4), since we have , the above requirement is possible
, the above requirement is possible
 (a)
(a) (b)
(b)
Figure 4. (a)  as a function
as a function ; (b)
; (b) as a function
as a function .
.
only when the change of  between two states is equal to an even integer number:
between two states is equal to an even integer number:
 . (5)
. (5)
We have said that in Li atom the ground state electron (2s electron) occupies the entangled state of  and
and  at
at . Therefore a photonic transition occurs either to the entangled states with
. Therefore a photonic transition occurs either to the entangled states with  or
or . In the present study we will consider only
. In the present study we will consider only  values up to 10. We will see that in this range (
values up to 10. We will see that in this range ( ) we get 26 different energy values which produce 325 wavelengths some of which are the same.
) we get 26 different energy values which produce 325 wavelengths some of which are the same.
2.4. Detailed Calculation of the Zeeman-Fine Energies of Li Atom
From the (NIST) values, the ionization energy of Li atom is , while the smallest amount of energy that allows a transition from the ground state to the nearest excited state(
, while the smallest amount of energy that allows a transition from the ground state to the nearest excited state(

 ) is equal to
) is equal to 
which corresponds to 6707.91 Å. In this transition the initial and the final value of  is the same and equal to unity:
is the same and equal to unity: . Therefore we can write
. Therefore we can write 
 Therefore from (2) the energies of the initial and final states are:
Therefore from (2) the energies of the initial and final states are:
 (6)
(6)
and
 (7)
(7)
respectively. The solutions of (6) and (7) gives us that 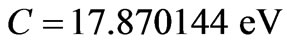 and
and . Substitution of these values in (2) gives the Zeeman-fine energies of Li atom:
. Substitution of these values in (2) gives the Zeeman-fine energies of Li atom:
 (8)
(8)
In the present study we will take  values in the range (
values in the range ( ). For each value of
). For each value of  substituting the values of
substituting the values of  and taking
and taking  we get 26 different energy values which are given in Table 1. These 26 different energy values give us 325 wavelengths some of which are the same. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values [14] for atomic Li (Figure 5). In Table 2, we give the comparison between the observed values and the corresponding calculated values which have Doppler shift-correction as well. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li.
we get 26 different energy values which are given in Table 1. These 26 different energy values give us 325 wavelengths some of which are the same. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values [14] for atomic Li (Figure 5). In Table 2, we give the comparison between the observed values and the corresponding calculated values which have Doppler shift-correction as well. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li.
2.5. Calculation of the Dopplershift for Li Atom
The above calculations are based on the assumption that the center of mass of the Li atom is at rest, but only the outermost electron is moving. But since the experimental


Table 1. Zeeman-fine Energies and related  values for
values for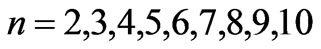 . (Here
. (Here  states are denoted by s,p,d,f,g,h,… respectively.)
states are denoted by s,p,d,f,g,h,… respectively.)
results are taken from the moving Li atom, there will be a small difference coming from the Doppler shift. To calculate the Doppler shift we take two different repeated wavelengths from the (NIST) database. For example if we  and
and . The corresponding calculated values are
. The corresponding calculated values are  and
and  respectively. Now we can calculate the average Doppler shift by using the above values:
respectively. Now we can calculate the average Doppler shift by using the above values:
 (9)
(9)
So the magnitude of the Doppler shift is found to be

Figure 5. A comparison between Doppler-shift corrected wavelengths ( ) and observed values.
) and observed values.


Table 2. Comparision between the observed and Dopplershift-corrected calculated wavelengths.
 . (10)
. (10)
3. Conclusions
We have calculated the effective Landé g-factors,  , related to the Zeeman-fine energies and the spectrum of the atomic Lithium (Li) by using the varying effective Landé g-factor method. It is shown the allowed values of
, related to the Zeeman-fine energies and the spectrum of the atomic Lithium (Li) by using the varying effective Landé g-factor method. It is shown the allowed values of  are restricted only with three odd integers (
are restricted only with three odd integers ( ) and this result is independent of the limit of the principle quantum number,
) and this result is independent of the limit of the principle quantum number, . In the present study we take the principle quantum number in the range; (
. In the present study we take the principle quantum number in the range; ( ). For this range we find 26 different energy values and 325 wavelengths some of which are the same. The present calculations are based on the assumption that the center of mass of the Li atom is at rest, but only the outermost electron is moving. But since the experimental results are taken from the moving Li atom, there will be a small difference coming from the Doppler shift. The Doppler shift is found to be
). For this range we find 26 different energy values and 325 wavelengths some of which are the same. The present calculations are based on the assumption that the center of mass of the Li atom is at rest, but only the outermost electron is moving. But since the experimental results are taken from the moving Li atom, there will be a small difference coming from the Doppler shift. The Doppler shift is found to be . The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li. The present results suggest new wavelengths such as
. The Doppler shift-corrected wavelengths are in perfect agreement with the observed (NIST) values for atomic Li. The present results suggest new wavelengths such as
 ,
,  and
and 
should be observed. Applications of the above treatment can give access to the production of new laser lights from atomic Lithium as well. Extending the range of  to (
to ( ) will allow us to calculate all the observed wavelengths for Li atom. A more detailed study will be presented in the future.
) will allow us to calculate all the observed wavelengths for Li atom. A more detailed study will be presented in the future.
REFERENCES
- P. J. Mohr, B. N. Taylor and D. B. Newel, “CODATA Recommended Values of the Fundamental Physical Constants: 2006,” Reviews of Modern Physics, Vol. 80, No. 2, 2008, pp. 633-730. doi:10.1103/RevModPhys.80.633
- R. C. Hilborn, “Einstein Coefficients, Cross Sections, F Values, Dipole Moments and All That,” American Journal of Physical, Vol. 50, 1982, pp. 982-986. doi:10.1119/1.12937
- D. J. Aurie and L. N. Adolph, “Lange’s Handbook of Chemistry,” McGraw-Hill, New York, 1998
- W. D. Phillips, “Laser Cooling and Trapping of Neutral Atoms,” Nobel Lecture, 8 December 1997
- D. E. Pritchard, “Cooling Neutral Atoms in a Magnetic Trap for Precision Spectroscopy,” Physical Review Letters, Vol. 51, No. 15, 1983, pp. 1336-1339. doi:10.1103/PhysRevLett.51.1336
- B. C. Sanders, “Entangled Coherent States,” Physical Review A, Vol. 45, No. 9, 1992, pp. 6811-6815. doi:10.1103/PhysRevA.45.6811
- A. Griffin, D. W. Snoke and S. Stringari, “Bose Einstein Condensation,” Cambridge University Press, Cambridge, 1995.
- L. G. Boussiakou, C. R. Bennett and M. Babiker, “Electrodynamics of Bose Einstein Condensates in Angular Motion,” Journal of Optics B, Vol. 4, 2002, pp. S25-S32.
- Z. Saglam, S. B. Bayram and M. Saglam, “Calculation of the Effective G-Factor for the (
 )
)  (
( )
) (
( ) Transitions in Hydrogen-Like Atoms and Its Application to the Atomic Cesium,” Journal of Modern Physics, Vol. 1, 2010, pp. 399-404.
) Transitions in Hydrogen-Like Atoms and Its Application to the Atomic Cesium,” Journal of Modern Physics, Vol. 1, 2010, pp. 399-404. - G. Sahin and M. Saglam, “Calculation of the Magnetic moment of the Photon,” Journal of Physics: Conference Series, Vol. 194, No. 2, 2009, p. 22006. doi:10.1088/1742-6596/194/2/022006
- M. Saglam and G. Sahin, “Photon in the Current Loop Model,” International Journal of Modern Physics, Vol. 23, No. 24, 2009, pp. 4977-4985. doi:10.1142/S0217979209053862
- M. Saglam and B. Boyacioglu, “The Absence of Decimal G-Factor in QHE Systems,” Physica Status Solidi B, Vol. 230, No. 1, 2002, pp. 133-142. doi:10.1002/1521-3951(200203)230:1<133::AID-PSSB133>3.0.CO;2-B
- M. Saglam, “Flux Quantization Associated with Electron Spin for Correlated Electron System in QHE,” Physica E, Vol. 17, 2003, pp. 345-346. doi:10.1016/S1386-9477(02)00800-7
- NIST Atomic Spectra Database. http://physics.nist.gov/asd
- M. Saglam, Z. Saglam, B. Boyacioglu and K. K. Wan, “Quantized Magnetic Flux through the Excited-State Orbits of Hydrogen Atom,” Journal of Russian Laser Research, Vol. 28, No. 3, 2007, pp. 267-271. doi:10.1007/s10946-007-0015-6

