Journal of Modern Physics
Vol.07 No.06(2016), Article ID:65297,6 pages
10.4236/jmp.2016.76058
Signature of Gravitational Waves in Stellar Spectroscopy
Shahen Hacyan
Instituto de Física, Universidad Nacional Autónoma de México, Ciudad de México, Mexico

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 16 January 2016; accepted 27 March 2016; published 31 March 2016
ABSTRACT
The possible detection of gravitational waves by interferometric observations of distant light sources is studied. It is shown that a gravitational wave affects the interferometric pattern of stellar light in a particular way. Michelson and Hanbury Brown-Twiss interferometers are considered, and it is shown that the latter is the most adequate for such a detection.
Keywords:
Gravitational Waves, Spectroscopy

1. Introduction
A gravitational wave (GW) could be detected indirectly by its interaction with the light emitted by astronomical objects. Thus, for instance, the passage of a GW produces a time delay in the signal received from distant sources (Estabrook and Wahlquist [1] ). Similarly, the presence of a stochastic background of GWs can be inferred from a statistical analysis of pulsar timing (Hellings and Downs [2] ). GWs can also interact with the polarization of electromagnetic waves (Hacyan [3] [4] ).
In this paper, we study the effect of GWs on the interferometry of stellar light. Two basic types of interfero- metric devices used in astronomy are considered: the Michelson (see, e.g., [5] ) and the Hanbury Brown-Twiss [6] interferometers. The former uses the interference between two signals, and the latter uses the interference between intensities of light. An intensity interferometer has, in general, some advantages over a Michelson interferometer. It will be shown in the following that the passage of a GW could be more easily detected by intensity interferometry.
Section 2 of the present paper is devoted to the analysis of an electromagnetic wave in the presence of a plane fronted GW. The analysis is based on previous works (Hacyan [3] [4] ) in which the form of the electromagnetic field is deduced using a short-wave length approximation. A general formula for the correlation of electric fields is obtained and the result is applied to interferometric analysis in Section 3; particular cases are worked out.
2. The Electromagnetic Field
The metric of a plane GW in the weak field limit is
 (1)
(1)
where the two degrees of polarization of the GW are given by the potentials 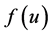 and
and , which are functions of u only. The relation with Minkowski coordinates t and z is
, which are functions of u only. The relation with Minkowski coordinates t and z is
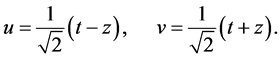
In the following, quadratic and higher order terms in f and g are neglected, and we set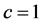 .
.
The direction of a light ray in the absence of a GW is k, with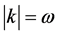 , the frequency of the (monochromatic) wave. We set
, the frequency of the (monochromatic) wave. We set
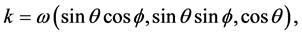
thus defining the angles  and
and . In the following, it will be convenient to define the functions
. In the following, it will be convenient to define the functions
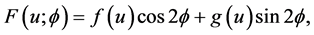 (2)
(2)
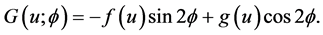 (3)
(3)
In the short-wave length approximation, the electromagnetic potential is taken as
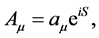
where S is the eikonal function satisfying the equation . Then,
. Then, 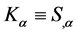 is a null-vector defining the direction of propagation of the electromagnetic wave, and
is a null-vector defining the direction of propagation of the electromagnetic wave, and 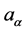 is a four-vector such that
is a four-vector such that
The electromagnetic vector is [4]

where 




and the eikonal function is
As in Ref. [4] , for a plane wave we use a gauge such that
where 
The four vector 




where 

Let us use a tetrad 




Accordingly the tetrad components of 


and

Notice in particular that

The electric field in tetrad components is

and of course
Correlations
For an electromagnetic plane wave with wave vector

where
are Stokes parameters (

3. Interferometry
Consider two detectors with space-time coordinates 




where


the subindexes a, b and j refer to the labels 1 and 2 of x and k.
A Michelson interferometer permits to measure the average intensity

where the second term is the interference term.
A Hanbury Brown-Twiss interferometer permits to measure the interference between intensities:

where the second term is the interference between the two intensities.
Define
With this notation, we have for a Michelson interferometer:

and for a Hanbury Brown-Twiss interferometer:

Define also the complex functions
and
Then

and

In the absence of GWs, 
implying that 

where





It should be noticed that the field correlation 

highly oscillatory and hinder a precise measurement with a Michelson interferometer. On the other hand, such terms do not appear in the correlation of the intensities:

The time dependence is included only in the terms 


3.1. Temporal Coherence
As a particular application of the above formulas, we can calculate the temporal coherence of a single signal in the presence of a GW. This can be obtained setting




and

Explicitly, in this particular case,

which is the only relevant term for the time correlation of the intensity correlation, and is entirely due to the GW.
3.2. Sinusoidal Waves and Pulses
In the particular case of a sinusoidal monochromatic GW of frequency

where 

As for a pulse of GW, it can be approximated by a delta function:



where 





4. Conclusion
The main conclusion from the present results is that the passage of a GW produces a time-dependent perturbation in the intensity interference of a distant light sources, an interference which would otherwise have a
static pattern. Thus, a time variation of 

Cite this paper
Shahen Hacyan, (2016) Signature of Gravitational Waves in Stellar Spectroscopy. Journal of Modern Physics,07,552-557. doi: 10.4236/jmp.2016.76058
References
- 1. Estabrook, G.S. and Wahlquist, H.D. (1975) General Relativity and Gravitation, 6, 439-447.
http://dx.doi.org/10.1007/BF00762449 - 2. Hellings, R.W. and Downs, G.S. (1983) The Astrophysical Journal, 265, L39-L42.
http://dx.doi.org/10.1086/183954 - 3. Hacyan, S. (2012) General Relativity and Gravitation, 44, 2923-2931.
http://dx.doi.org/10.1007/s10714-012-1434-4 - 4. Hacyan, S. (2016) International Journal of Modern Physics A, 31, 1641023, 8 p.
http://dx.doi.org/10.1142/S0217751X16410232 - 5. Hariharan, P. (2007) Basics of Interferometry. 2nd Edition, Elsevier, Amsterdam.
- 6. Hanbury Brown, R. and Twiss, R.Q. (1956) Nature, 178, 1046-1048.
http://dx.doi.org/10.1038/1781046a0













