Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19993 , 4 pages DOI:10.4236/am.2012.37110
On the Derivative of a Polynomial
P.G. Department of Mathematics, Kashmir University, Srinagar, India
Email: {dr.narather, mushtaqa022}@gmail.com
Received May 2, 2012; revised June 2, 2012; accepted June 9, 2012
Keywords: Polynomials; Inequalities; Complex Domain
ABSTRACT
Certain refinements and generalizations of some well known inequalities concerning the polynomials and their derivatives are obtained.
1. Introduction to the Statement of Results
Let 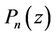 denote the space of all complex polynomials
denote the space of all complex polynomials 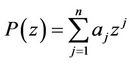 of degree n. If
of degree n. If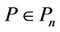 , then
, then
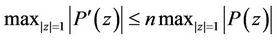 (1)
(1)
and
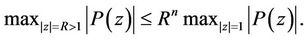 (2)
(2)
Inequality (1) is an immediate consequence of S.Bernstein’s theorem (see [1]) on the derivative of a trigonometric polynomial. Inequality (2) is a simple deduction from the maximum modulus principle (see [2, p. 346] or [3, p. 137]).
Both the inequalities (1) and (2) are sharp and the equality in (1) and (2) holds if and only if 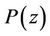 has all its zeros at the origin. It was shown by Frappier, Rahman and Ruscheweyh [4, Theorem 8] that if
has all its zeros at the origin. It was shown by Frappier, Rahman and Ruscheweyh [4, Theorem 8] that if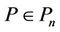 , then
, then
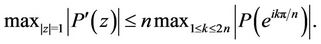 (3)
(3)
Clearly (3) represents a refinement of (1), since the maximum of 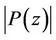 on
on 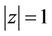 may be larger than the maximum of
may be larger than the maximum of 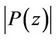 taken over
taken over 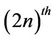 roots of unityas is shown by the simple example
roots of unityas is shown by the simple example ,
, .
.
A. Aziz [5] showed that the bound in (3) can be considerably improved. In fact proved that if , then for every given real
, then for every given real ,
,
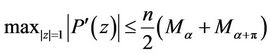 (4)
(4)
where
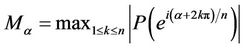 (5)
(5)
and 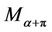 is obtained by replacing
is obtained by replacing 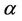 by
by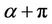 . The result is best possible and equality in (4) holds for
. The result is best possible and equality in (4) holds for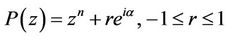 .
.
Clearly inequality (4) is an interesting refinement of inequality (3) and hence of Bernstein inequality (1) as well.
If we restrict ourselves to the class of polynomials 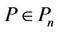 having no zero in
having no zero in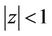 , then the inequality (1) can be sharpened. In fact, P. Erdös conjectured and later P. D. Lax [6] (see also [7]) verified that if
, then the inequality (1) can be sharpened. In fact, P. Erdös conjectured and later P. D. Lax [6] (see also [7]) verified that if 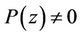 for
for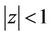 , then (1) can be replaced by
, then (1) can be replaced by
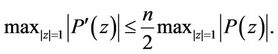 (6)
(6)
In this connection A. Aziz [5], improved the inequality (4) by showing that if 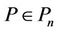 and
and 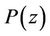 does not vanish in
does not vanish in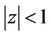 , then for every real
, then for every real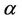 ,
,
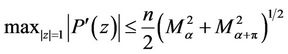 (7)
(7)
where 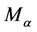 is defined by (5). The result is best possible and equality in (7) holds for
is defined by (5). The result is best possible and equality in (7) holds for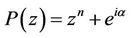 .
.
A. Aziz [5] also proved that if 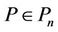 and
and 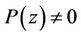 in
in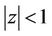 , then for every real
, then for every real 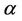 and
and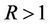 ,
,
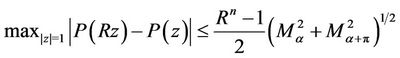 (8)
(8)
In this paper, we first present the following result which is a refinement of inequality (7).
Theorem 1. If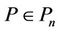 ,
, 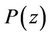 does not vanish in
does not vanish in
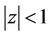 and
and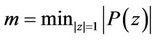 , then for every real
, then for every real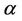 ,
,
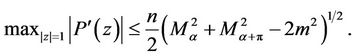 (9)
(9)
where 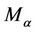 is defined by (5). The result is best possible and equality in (9) holds for
is defined by (5). The result is best possible and equality in (9) holds for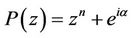 .
.
As an application of Theorem 1, we mention the corresponding improvement of (8).
Theorem 2. If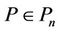 , and
, and 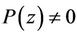 for
for 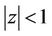 and
and 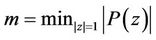 then for every real
then for every real 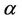 and
and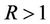 ,
,
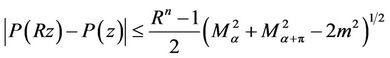 (10)
(10)
where 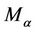 is defined by (5). The result is best possible and equality in (10) holds for
is defined by (5). The result is best possible and equality in (10) holds for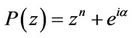 .
.
Here we also consider the class of polynomials 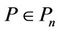 having no zero in
having no zero in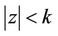 ,
, 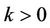 and present some generalizations of the inequalities (9) and (10). First we consider the case
and present some generalizations of the inequalities (9) and (10). First we consider the case 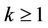 and prove the following result which is a generalization of inequality (9).
and prove the following result which is a generalization of inequality (9).
Theorem 3. If 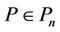 does not vanish in
does not vanish in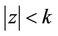 ,
, 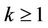 and
and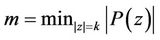 , then for every real
, then for every real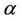 ,
,
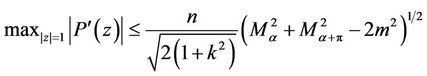 (11)
(11)
where 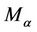 is defined by (5).
is defined by (5).
Next result is a corresponding generalization of the inequality (10).
Theorem 4. If 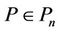 does not vanish in
does not vanish in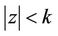 ,
, 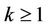 and
and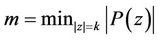 , then for every real
, then for every real 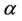 and
and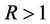 ,
,
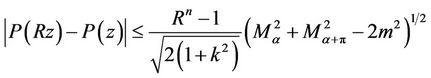 (12)
(12)
where 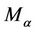 is defined by (5).
is defined by (5).
Remark 1. For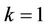 , Theorem 3 and Theorem 4 reduces to the Theorem 1 and Theorem 2 respectively.
, Theorem 3 and Theorem 4 reduces to the Theorem 1 and Theorem 2 respectively.
For the case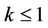 , we have been able to prove:
, we have been able to prove:
Theorem 5. If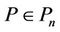 ,
, 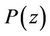 has no zero in
has no zero in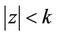 ,
, 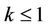 and
and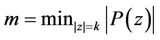 , then for every real
, then for every real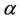 ,
,
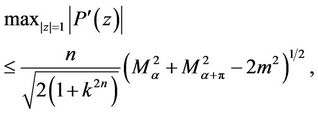 (13)
(13)
provided 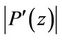 and
and 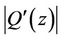 attain maximum at the same point on
attain maximum at the same point on 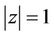 where
where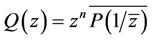 . The result is best possible and equality in (13) holds for
. The result is best possible and equality in (13) holds for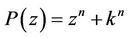 .
.
Theorem 6. If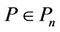 ,
, 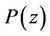 has no zero in
has no zero in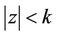 ,
,
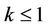 and
and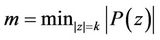 , then for every real
, then for every real 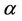 and
and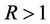 ,
,
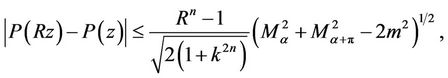 (14)
(14)
provided 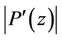 and
and 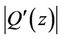 attain maximum at the same point on
attain maximum at the same point on 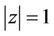 where
where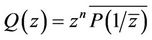 . The result is best possible and equality in (14) holds for
. The result is best possible and equality in (14) holds for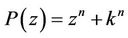 .
.
2. Lemmas
For the proofs of these theorems, we need the following lemmas. The first Lemma is due to A. Aziz [5].
Lemma 1. If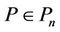 , then for
, then for 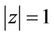 and for every real
and for every real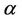 ,
,
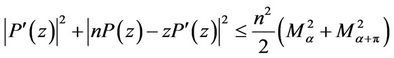 (15)
(15)
where 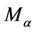 is defined by (5).
is defined by (5).
Lemma 2. If 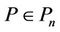 and
and 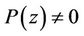 for
for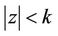 ,
, 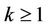 , then for
, then for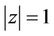 ,
,
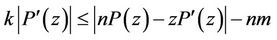
where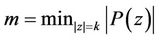 .
.
Lemma 2 is a special cases of a result due to A. Aziz and N. A. Rather [8, Lemma 5].
Lemma 3. If 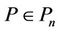 does not vanish in
does not vanish in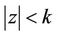 ,
, 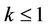 , then
, then
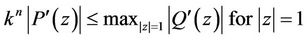
where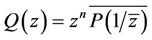 .
.
This Lemma is due to N. K. Govil [9].
Lemma 4. If 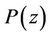 is a polynomial of degree n which does not vanish in
is a polynomial of degree n which does not vanish in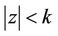 ,
, 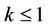 , then for
, then for 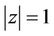
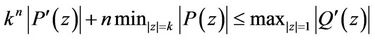
where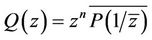 .
.
Proof of Lemma 4. Let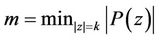 . If
. If 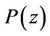
has a zero on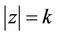 , then
, then 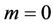 and the result follows from Lemma 3. Henceforth we assume that
and the result follows from Lemma 3. Henceforth we assume that 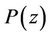 has no zero on
has no zero on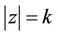 , therefore
, therefore 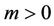 and
and
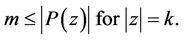
If 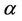 is any real or complex number with
is any real or complex number with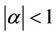 , then for
, then for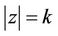 ,
,
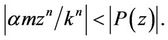
By Rouche’s Theorem, it follows that the polynomial 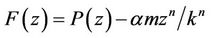 does not vanish in
does not vanish in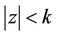 , for every real or complex number
, for every real or complex number 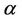 with
with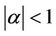 . Applying Lemma 3 to the polynomial
. Applying Lemma 3 to the polynomial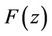 , we get
, we get
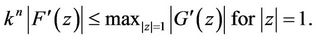 (16)
(16)
where
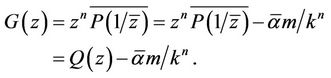
Replacing 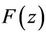 by
by 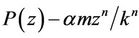 and
and 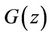 by
by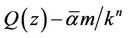 , we obtain from (16) for
, we obtain from (16) for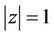 ,
,
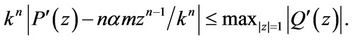 (17)
(17)
Now choosing the argument of 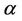 in the left hand side of (17) such that
in the left hand side of (17) such that
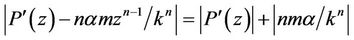
we obtain for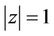 ,
,
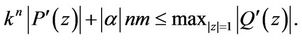
Letting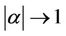 , we get the desired result. This proves Lemma 4.
, we get the desired result. This proves Lemma 4.
3. Proof of the Theorems
Proof of Theorem 1. By hypothesis 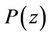 does not vanish in
does not vanish in 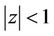 and
and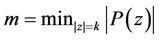 , therefore, by Lemma 2 with
, therefore, by Lemma 2 with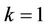 , we have
, we have
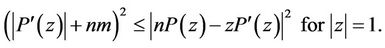
This gives with the help of Lemma 1
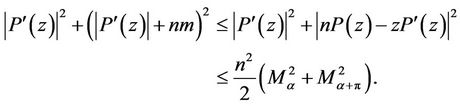
Since
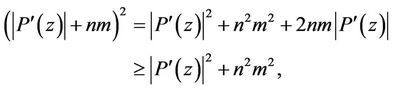
it follows that
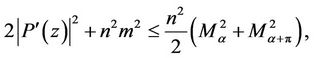
which implies for 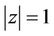
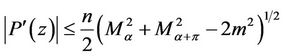
and hence
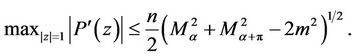
This completes the proof of Theorem 1.
Proof of Theorem 2. Applying (2) to the polynomial 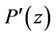 which is of degree
which is of degree 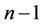 and using Theorem 1, we obtain for
and using Theorem 1, we obtain for 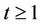 and
and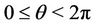 ,
,
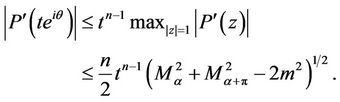
Hence for each 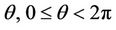 and
and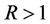 , we have
, we have
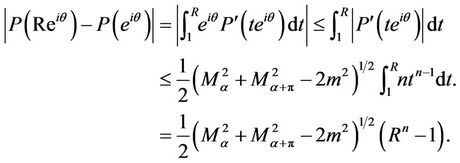
This implies for 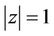 and
and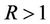 ,
,
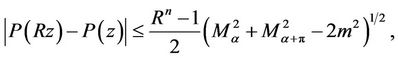
which proves Theorem 2.
The proof of the Theorem 3 and 4 follows on the same lines as that of Theorems 1 and 2, so we omit the details.
Proof of Theorem 5. Since all the zeros of 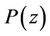 lie in
lie in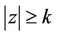 , where
, where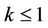 ,
, 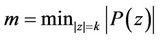 , by Lemma 4, we have
, by Lemma 4, we have
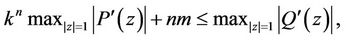 (18)
(18)
where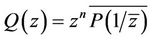 . Also by hypothesis
. Also by hypothesis 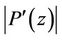 and
and 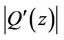 become maximum at the same point on
become maximum at the same point on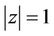 , if
, if
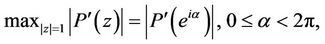 (19)
(19)
then
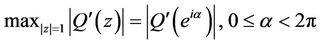 (20)
(20)
and it can be easily verified that
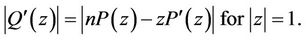
Therefore, by Lemma 1
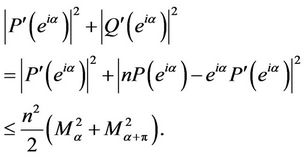
This gives with the help of (18), (19) and (20) that
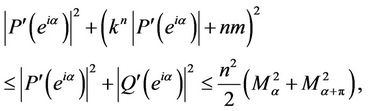
which implies,
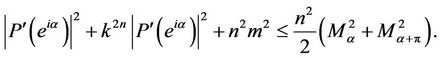
Equivalently,
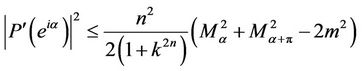
and hence
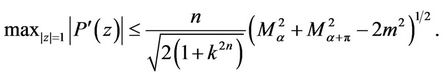
This completes the proof of Theorem 5.
Theorem 6 follows on the same lines as that of Theorem 2, so we omit the details.
REFERENCES
- A. C. Schaffer, “Inequalities of A. Markoff and S. Bernstein for Polynomials and Related Functions,” Bulletin of the American Mathematical Society, Vol. 47, 1941, pp. 565-579. doi:10.1090/S0002-9904-1941-07510-5
- M. Riesz, “Uber Einen Satz des Herrn Serge Bernstein,” Acta Mathematica, Vol. 40, 1916, pp. 337-347. doi:10.1007/BF02418550
- G. Pólya and G. Szegö, “Aufgaben und lehrsätze aus der Analysis,” Springer-Verlag, Berlin, 1925.
- C. Frappier, Q. I. Rahman and St. Ruscheweyh, “New Inequalities for Polynomials,” Transactions of the American Mathematical Society, Vol. 288, 1985, pp. 69-99. doi:10.1090/S0002-9947-1985-0773048-1
- A. Aziz, “A Refinement of an Inequality of S.Bernstein,” Journal of Mathematical Analysis and Applications, Vol. 142, No. 1, 1989, pp. 226-235. doi:10.1016/0022-247X(89)90370-3
- P. D. Lax, “Proof of a Conjecture of P.Erdös on the Derivative of a Polynomial,” Bulletin of the American Mathematical Society, Vol. 50, 1944, pp. 509-513. doi:10.1090/S0002-9904-1944-08177-9
- A. Aziz and Q. G. Mohammad, “Simple Proof of a Theorem of Erdos and Lax,” Proceedings of the American Mathematical Society, Vol. 80, 1980, pp. 119-122.
- A. Aziz and N. A. Rather, “New Lq Inequalities for Polynomials,” Mathematical Inequalities and Applications, Vol. 2, 1998, pp. 177-191. doi:10.7153/mia-01-16
- N. K. Govil and Q. I. Rahman, “Functions of Exponential Type Not Vanishing in a Half Plane and Related Polynomials,” Transactions of the American Mathematical Society, Vol. 137, 1969, pp. 501-517. doi:10.1090/S0002-9947-1969-0236385-6

