World Journal of Condensed Matter Physics
Vol.3 No.1(2013), Article ID:28270,8 pages DOI:10.4236/wjcmp.2013.31001
Structural and Magnetic Properties of Substituted Delafossite-Type Oxides CuCr1−xScxO2
![]()
1Laboratory of Material Sciences and Environnement, Faculty of Science of Sfax, Sfax, Tunisia; 2Unit of Material chemistry Research, University of Tunis Elmanar, Tunis, Tunisie; 3Neel Institute, CNRS, Grenoble, France.
Email: *mongi.amami@ipein.rnu.tn
Received July 28th, 2012; revised September 29th, 2012; accepted October 11th, 2012
Keywords: Delafossite; XRD; Raman Spectroscopy; Magnetism
ABSTRACT
This work describes the scandium doping effect on the structural and magnetic properties of delafossite-type oxides CuCr1−xScxO2. The lattice parameters were found to vary according to Vegard’s low. A reflection broadening is observed, that is ascribed to local lattice distortion due to the ionic radius difference between Cr3+ and the non-magnetic dopants. Magnetic susceptibility measurements show that the dominant interactions are antiferromagnetic (AFM) but that doping induces significant changes. The coupling between the local spins at the Cr sites and doped metal transition may enhance spin fluctuations at the Cr sites, which break the residual magnetic degeneracy as fluctuation-induced symmetry breaking in a highly magnetic degenerate ground state manifold of some frustrated systems.
1. Introduction
The family of layered oxides generally referred to as delafossites derive their name from the mineral CuFeO2 [1], with which their crystal structures are isotypic. Denoted by the general chemical formula ABO2, the crystal structures of these materials (Figure 1) are characterized by layers of distorted, edge-sharing octahedra with oxygen coordinating metal cations (B = typically transition or group 13 elements, but also some rare earth species), separated by planar layers of a transition metal (A = typically Cu, Ag, Pd or Pt) which are linearly coordinated along the c-axis by two oxygen sites. The stacking orientation of these two layers results in two basic polymorphs, 2H (space group P 63/mmc) and 3R (space group R-3m), (Figure 1). Characterized by a wide range of possible compositions, the delafossite oxides also exhibit significant richness in properties. For example, depending upon the choice of A, compounds can display metallic (A = Pd, Pt) or semiconducting/insulating (A = Cu, Ag) behavior [2]. Motivated by the relatively high electrical conductivities observed in some delafossite compounds [2-5], in particular observations [3,4] of ptype conductivity and relatively high optical transparency in CuAlO2 thin films, significant efforts in recent years have been focused on the usage of these materials in applications as transparent conductors [5].
Copper-scandium oxide (CSO) is a p-type transparent Cu+-based oxide with a delafossite structure. Holes in CSO are introduced by substituting divalent species for the octahedral Sc-sites and by intercalating with excess oxygen near the Cu+ planes. CSO has the smallest Cu-Cu distance for which excess oxygen intercalation is possible between the layers of Cu [6,7]. In Cu+-based delafossites, the Cu-Cu distances significantly affect the electri-

Figure 1. Delafossite structure (3R) and (2H).
cal conductivity, because holes predominantly pass through the Cu+ planes [7]. Therefore, CSO potentially has the highest p-type electrical conductivity in transparent Cu+- based delafossites. From a crystallographic point of view, CSO has two crystalline phases depending on the stacking periods along the c -axis: rhombohedral (CSO (3R)) and hexagonal (CSO (2H)) [6,7]. The a-axis lattice constants of each phase are 0.3216 nm for CSO (3R) [8] and 0.3215 nm for CSO (2H) [9] and they are very close to that of ZnO (0.3250 nm) [10]. Since ZnO is an n-type transparent conducting oxide with a hexagonal crystalline structure, transparent p-n heterojunctions with excellent interfaces can be fabricated with CSO (0 0 01)/ ZnO (0 0 01) epitaxial films.
CuCrO2 is also reported to exhibit both antiferromagnetic [11] and ferroelectric [12] behavior below its Néel temperature, T = 25 K. The magnetic structure and the mechanism responsible for the ferroelectricity are still under investigation. Recently we report, on the effect of Sc and (Sc + Mg) substitution on the structural and physical properties of delafossite-type CuCrO2 oxide [13]. The present study intends to study in detail the effect of the substitution of Sc3+ for Cr3+ in the widest possible substitution range on the structural, spectroscopic and magnetic properties of CuCr1−xScxO2 0 ≤ x ≤ 0.4.
2. Experimental Details
First, polycrystalline samples of CuCr1−xScxO2 0 ≤ x ≤ 0.4 were prepared by using the standard solid-state reaction. Stoichiometric mixtures (0.5 g) of Cu2O, Cr2O3 Sc2O3 were ground and pressed into pellets, which were set in alumina crucible. The samples were fired several times at 1050˚C for 12 h. The X-ray powder diffraction patterns of the reacted pellets were collected with a PANalytical diffractometer equipped with a CuKα source (Kα1 and Kα2) in the 2q range from 10˚ to 90˚ at room temperature.
Strain and size components were extracted from line widths using the Williamson-Hall (WH) analysis [14]. This method uses the fact that the crystallite size contribution varies as tanθ. The equation used is

Where L is the integral width, λ is the wavelength used, D is the size of the coherent diffraction domain, k is a near-unity constant, and e is the microstrain term. As a result, a plot of (L∙cosq ) as a function of (sinq) yields D from the constant term and e from the slope.
Magnetization dependence on temperature was measured in a Superconducting quantum Interference Device (SQUID) magnetometer while heating from 2.0 to 300 K in 0.1 T.
The Raman spectra were recorded at room temperature with the 514.5 nm line of an Ar+ laser, excitation from a Spectra Physics krypton ion laser. The compounds were studied with a low laser power (102 mW). One scanning of 60 seconds has been used for each spectral range. No damage of the material by the laser has been observed. The beam was focused onto the samples using the macroscopic configuration of the apparatus.
3. Results and Discussions
3.1. Structural Characterizations
The crystal structure of CuCr1−xScxO2 (0 £ x £ 0.4) samples is determined by recording x-ray diffraction patterns shown in Figure 2. According to the standard XRD patterns of CuCrO2 samples they are of single phase with delafossite structure (space group R-3m), without any detectable secondary phase up to 20% Sc content. Above this composition a shoulder like shape appear around 34 in 2q, which increase in intensity with the Sc content. The deconvolution of the observed shoulder points award an overlapping of two peaks (inset of Figure 2), which were assigned to the CuScO2 (3R) and CuScO2 (2H). A mixed-layer form of CuScO2 (intergrown 3R and 2H) generally results when heating mixtures of equimolar amounts of Cu2O and Sc2O3 under various conditions [15]. These mixed-layer products were dominated by a 3R type structure with stacking faults of the 2H type.
In addition, Figure 2 clearly shows that 00l peaks are sharp, but other (h0l) peaks are broadened, shifted and asymmetric due to stacking faults perpendicular to the c axis. In the sample CuCr0.6Sc0.4O2, the peaks broadening are very important in a way that the phase identification is risky. Considering the differences in the radii of Cr3+ (0.615 Å) and Sc3+ (0.75 Å) [16], the possibility of substituting Cr ion by the Sc in the full range 0 < x < 1 is surprising. As a condition for isomorphous miscibility, Vegard’s rule [17] allows deviations in the different radii only up to 15%. In the present case the deviation between Cr3+ and Sc3+ is about 22%. At this percentage, the two secondary phases are appeared. This fact accounts well for a high stabilization potential of the delafossite structure.
Composition dependences of the unit cell volume and lattice constants are given in Table 1 and displayed in Figure 3. For x = 0 (pure CuCrO2) our a and c parameter values are in very good agreement with most of those previously reported for powders as well as for single crystal (e.g. a = 2.9741 (1) Å, c = 17.110 (2) Å from [18]).
The increase of the unit cell volume with increasing x well agrees with the increase of the ionic radius as chromium (r = 0.615 Å) is substituted for scandium (r = 0.75 Å). However, the change is rather anisotropic as it is mainly due to the shrinking of the a parameter whereas

Figure 2. Room temperature XRD patterns of CuCr1−xScxO2 (0 ≤ x ≤ 0.3) samples with a rhombohedral delafossite structure.
Table 1. Cell parameter evolution with Sc content.

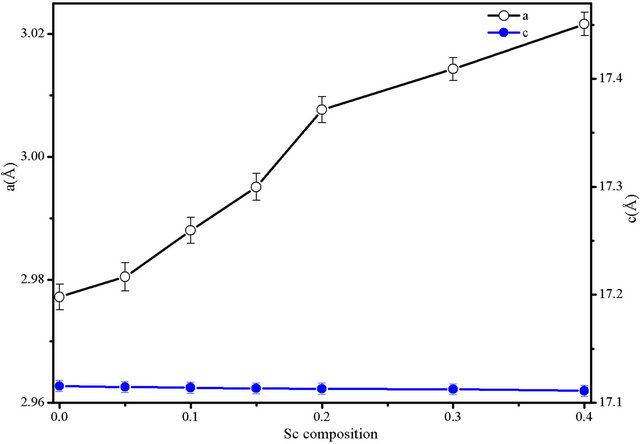
Figure 3. lattice constants evolution with the Sc content.
the c parameter remains more or less constant.
As the Cu-O distance does not vary much in delafossite, this tendency reflects a flattening of the MO6 octahedra. A nice geometric account of this evolution is given by J. Tate et al. [19] where the authors suggest that the strong repulsion between M3+ ions across the octahedron shared edges reduces the O-O distance to the contact distance.
Therefore the increase of the size of M cation leads to an increase of the octahedron distortion and in turn of the M-M distance that corresponds to the a parameter. We may recall that in CuMO2, as M changes from Al3+ to La3+ [20,21], the a parameter undergoes a huge increase from 2.8 up to 3.8 Å.
Strain generated by the Sc substitution was determined from the Williamson-Hall relationship. Plots of (L∙cosθ) as a function of (sinθ) are given in Figure 4. They show a remarkable difference in angular dependence of the line width for different families of inter reticular planes: the h0l planes yield an important contribution of microstrains (high slope), while this effect is almost negligible in 00l planes. This shows that this material behaves rather anisotropically, and that strains affects mostly bonding in the basal (ab) planes.
Finally note that the oxygen stoichiometry cannot be reliably obtained by X-ray diffraction data, and the presence of three different mixed-valences precludes a reliable use of chemical redox titration. However, all the samples being prepared in the same conditions (initial oxygen stoichiometry, amount of powder) and their oxygen content is assumed to close to 2 in all cases. This assumption is supported by a previous study of CuCrO2 showing that this compound does not accommodate large oxygen off-stoichiometry [22]. This could be confirmed by neutron diffraction, which was not available to us during this study.
3.2. Raman Spectroscopy
The delafossite structure belongs to point group C3v and space group R-3m. The four atoms in the primitive cell of its rhombohedral R-3m structure give rise to 12 optical phonon modes (Γ = A1g + Eg + 3A2u + 3Eu) in the zone center (k ~ 0): three acoustic and nine optical modes. Among these, the two phonons modes with A1g and Eg symmetry are Raman-active. The former arises due to the Cu-O bond vibration along the c-axis, whereas the doubly degenerate E-modes describe the vibration along the a-axis. Since there is only one mode of each symmetry, the exact eigenvector is determined without any lattice dynamical model required. Pellicer-Porres et al. [23-25] have discussed the phonon dispersion at the zone center for CuGaO2 delafossite. They proposed that the inversion center is lost along the ΓT direction and the symmetry is reduced from D3d to C3v. According to compatibility relations, A1g and A2u on one hand and Eg and Eu modes on the other transform to A1 and E-modes, respectively.
Figure 5 shows the Raman spectra of CuCr1−xScxO2 for different scandium content using a 514.5 nm laser wavelength excitation. The Raman spectrum of CuCrO2
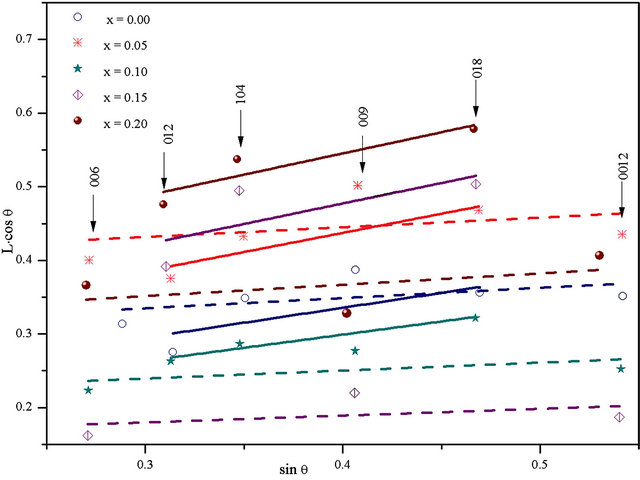
Figure 4. Williamson-Hall plot of integral line width L for different Sc concentration.
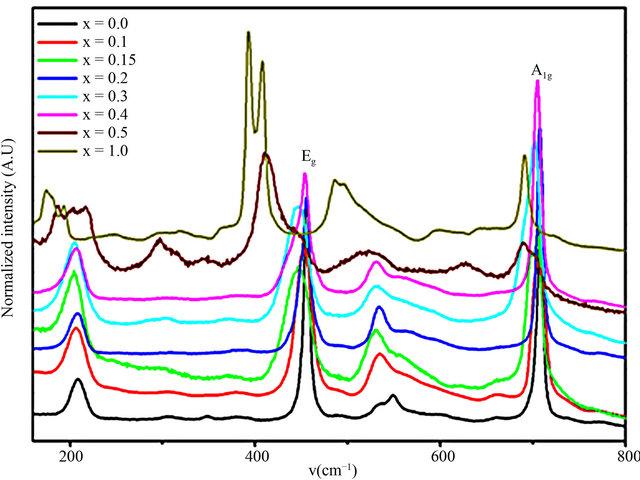
Figure 5. Raman spectroscopy of CuCr1−xScxO2 (0.0 ≤ x ≤ 0.5) bulk samples at room temperature.
exhibit three typical vibrational bands of delafossite structure, in agreement with earlier results on CuAlO2 [25] and CuGaO2[23]. These bands are identified as σ(A1g) at 691 cm−1, σ(Eg) at 444 cm−1 and σ(Ag) at 207 cm−1 (see Figure 5). It has been suggested that these vibrations may be associated with the spectral features of edge-sharing CrIIIO6 octahedra and possibly the O-CuI-O linear bond [26]. As shown in Figure 5, Scandium substitution induces abrupt changes in frequency and in line width of the A1g and Eg modes. The frequencies shift to shorter wavenumbers, indicating a weakening of (Cr,Sc)-O bonding, and is consistent with the observed lattice expansion along the different axes and the difference in ionic radius between Cr3+ and Sc3+. The A1g mode, in particular, is shifted by up 33 cm−1 upon Sc substitution; its frequency is thus very sensitive to B-site atom-oxygen bonding characteristics.
Starting from x = 0.05, we also note a strong increase in intensity of the initially weak band around 535 cm−1. Stronger changes begin at x = 0.3, where the A1g-Eg mode magnitude ratio is reverted and shoulders appear on several bands. We suggest that these features are related to increased disorder.
These results confirm that the substitution of Cr by Sc in the investigated concentration range of the CuCr1−xScxO2 compound is possible without the change of delafossite structure. However, local changes do arise, and they are much more relevant in Raman spectroscopy, that is a local probe, more than X-ray diffraction, where the effects of cationic composition changes are averaged and show up mainly as peak broadening.
3.3. Magnetic Properties
We performed the zero-field cooling (ZFC) measurements and the data are shown in Figure 6, where a 0.1 T magnetic field was applied. It can be clearly seen that all the samples are in the paramagnetic states in the temperature range 60 - 300 K.
For x = 0.00, an anomaly appears at 25 K owing to an antiferromagnetic (AFM) transition. The Néel temperature (TN) is almost consistent with the one previously reported [27]. The magnetic behaviour of Cu-Cr delafossite is very sensitive to the scandium content.
In fact the M-T curves, AFM contribution shows up in 5% Sc-doped samples only as a tiny anomaly in M(T) at about 30 K, which is due to the AFM interaction. These doping induced changes are qualitatively different from those for the Rh3+ and Co3+ dopants and are consistent with a pure randomness effect [28].
For x ³ 0.1 no abrupt increase of the magnetization was observed. Samples exhibit a weak paramagnetism varying slightly with temperature. Anomaly around 120 K for x = 0.1 is perhaps due to a very small amount (<0.01%) of magnetic impurity CuCr2O4. Such behavior was reported for Al-doped CuCrO2, however, above 20% Al content [20].
The spin dynamics of the geometrically frustrated triangular antiferromagnet multiferroic CuCrO2 has been mapped out using inelastic neutron scattering [12]. They determined the relevant spin Hamiltonian parameters, showing that the helicoidal model with a strong planar anisotropy correctly describes the spin dynamics. The

Figure 6. Temperature (T) dependence of zero-fieldcooling susceptibility of CuCr1−xScxO2 for 0.0 ≤ x ≤ 0.5 at 0.1 T.
weakly dispersive excitation along c reflects the 2D character of the magnetic interactions, but the spin dynamics in CuCrO2 clearly point out the relevance of the next-nearest-neighbor interaction to stabilize the magnetic order.
As x increases in CuCr1−xScxO2, in addition to strain effects, the number of magnetic nearest neighbors decreases and the onset of magnetic ordering is no longer seen in the plot of the reciprocal magnetic susceptibility versus temperature for x ≥ 0.1.
Replacing Cr3+ by a non magnetic Sc3+ seems to affect the coupling between in-plane next-nearest-neighbors interpreted as the signature of a slight deformation of the perfect triangular lattice.
The plot of  versus temperature (Figure 7) shows an exactly linear relation at high temperature, which is well fitted by the Curie-Weiss equation
versus temperature (Figure 7) shows an exactly linear relation at high temperature, which is well fitted by the Curie-Weiss equation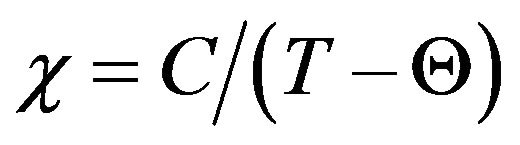 , where C and Q are the Curie-Weiss constant and magnetic coupling parameter, respectively.
, where C and Q are the Curie-Weiss constant and magnetic coupling parameter, respectively.
Fits with the Curie-Weiss equation using Origin program yield values of C and Q given in Table 2. All data yield highly negative Θ values, indicating dominant antiferromagnetic interactions. An effective moment by formula unit can be extracted using the formula
 (1)
(1)
where kB = Boltzmann constant, C = Curie constant, N = Avogadro’s number, µB = Bohr magneton. In the spinonly picture usually followed for localized spins of 3d ions, μeff is given by
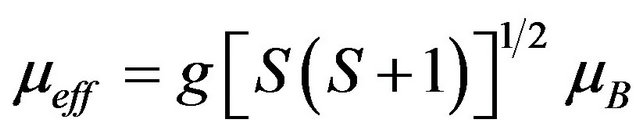 (2)
(2)
where g ≈ 2.0. The experimental values of µeff are all slightly lower than the theoretical spin-only value for Cr3+ , These results are consistent with the behaviour commonly observed for 3d cations, where the incomplete quenching of orbital moments yields lower values of μeff .The evolution of C with the scandium content points award a magnetic dilution effect.
, These results are consistent with the behaviour commonly observed for 3d cations, where the incomplete quenching of orbital moments yields lower values of μeff .The evolution of C with the scandium content points award a magnetic dilution effect.
4. Conclusion
After introducing Sc into the Cr lattice sites in alternating ab layers has a significant effect on the structure. The occupied Cr 3d states interact covalently with the neighboring O atoms and hence indirectly modify the Cu 3d states, an effect which the 3p6 Sc atoms are unable to produce. This decreases the density of states at the top of the valence band, which are precisely those states expected to determine the mobility of p-type charge carriers formed on doping. Temperature dependence of the magnetic susceptibility shows that a long range order takes place at low temperature for x ≤ 0.05. For higher dilution rates of magnetic ions (x ≥ 0.10) the temperature dependence of the magnetic susceptibility no longer ac-
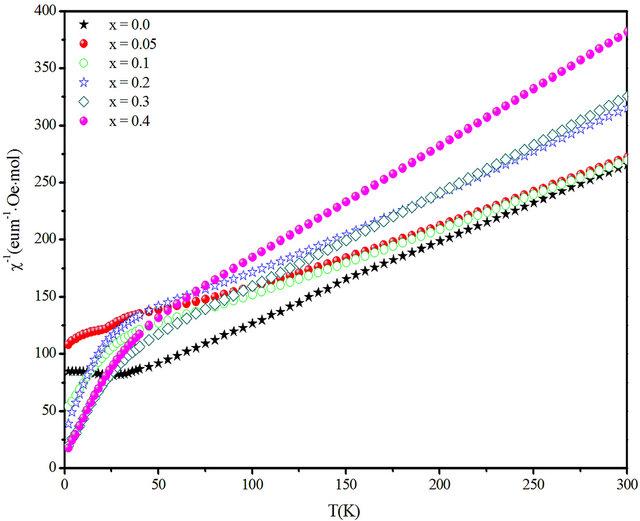
Figure 7. temperature dependence of the inverse susceptibility of CuCr1−xScxO2 as a function of the temperature.
Table 2. estimated Curie constant and Curie temperature from the high temperature paramagnetic region for CuCr1−xScxO2.

counts for long range ordering at least above 4 K.
5. Acknowledgements
The authors thank Université Joseph Fourier de Chimie, Grenoble for financial support.
REFERENCES
- C. Friedel, “A Combination of Natural Iron Oxides and Copper and Reproduction of Actamides,” Report of Sciences. Sciences Academy, Vol. 77, 1873, p. 211.
- D. B. Rogers, R. D. Shannon, C. T. Prewitt and J. L. Gillson, “Chemistry of Noble Metal Oxides. III. Electrical Transport Properties and Crystal Chemistry of ABO2 Compounds with the Delafossite Structure,” Inorganic Chemistry, Vol. 10, No. 4, 1971, pp. 723-727. doi:10.1021/ic50098a013
- H. Kawazoe, M. Yasukawa, H. Hyodo, M. Kurita, H. Yanagi and H. Hosono, “p-Type Electrical Conduction in Transparent Thin Films of CuAlO2,” Nature, Vol. 389, 1997, pp. 939-942. doi:10.1038/40087
- H. Yanagi, S. Inoue, K. Ueda, H. Kawazoe and H. Hosono, “Electronic Structure and Optoelectronic Properties of Transparent p-Type Conducting CuAlO2,” Journal of Applied Physics, Vol. 88, No. 7, 2000, pp. 4159-4164. doi:10.1063/1.1308103
- M. Marquardt, N. Ashmore and D. Cann, “Crystal Chemistry and Electrical Properties of the Delafossite Structure,” Thin Solid Films, Vol. 496, No. 1, 2006, pp. 146- 156. doi:10.1016/j.tsf.2005.08.316
- R. Kykyneshi, B. Nielsen, J. Tate, J. Li and A. Sleight, “Structural and Transport Properties of CuSc1−xMgxO2+y Delafossites,” Journal of Applied Physics, Vol. 96, No. 11, 2004, pp. 6188-6195. doi:10.1063/1.1806256
- J. Li, A. F. T. Yokochi and A. W. Sleight, “Oxygen Intercalation of Two Polymorphs of CuScO2,” Journal of Solid State Sciences, Vol. 6, No. 8, 2004, pp. 831-839. doi:10.1016/j.solidstatesciences.2004.04.015
- J. Doumerc, A. Ammar, A. Wichainchai, M. Pouchard and P. Hagenmuller, “Sur Quelques Nouveaux Composes de Structure de Type Delafossite,” Journal of Physical Chemistry of Solids, Vol. 48, No. 1, 1987, pp. 37-43.
- J. Li, A. Yokochi, T. Amos and A. Sleight, “Strong Negative Thermal Expansion along the O-Cu-O Linkage in CuScO2,” Chemistry of Materials, Vol. 14, No. 6, 2002, pp. 2602-2606.
- P. Fons, K. Iwata, S. Niki, A. Yamada, K. Matsubara and M. Watanabe, “Uniaxial Locked Growth of High-Quality Epitaxial ZnO Films on (1 1 2̄ 0)α-Al2O3,” Journal of Crystal Growth, Vol. 209, No. 2-3, 2000, pp. 532-536. doi:10.1016/S0022-0248(99)00614-4
- R. N. Attili, M. Uhrmacher, K. P. Lieb, L. Ziegeler, M. Mekata and E. Schwarz Mann, “Electric-Field Gradients at 111Cd in Delafossite Oxides ABO2 (A = Ag, Cu; B = Al, Cr, Fe, In, Nd, Y),” Physical Review B, Vol. 53, No. 2, 1996, pp. 600-608. doi:10.1103/PhysRevB.53.600
- S. Seki, Y. Onose and Y. Tokura, “Spin-Driven Ferroelectricity in Triangular Lattice Antiferromagnets ACrO2 (A = Cu, Ag, Li, or Na)”, Physical Review Letter, Vol. 101, No. 6, 2008, pp. 67204-67208. doi:10.1103/PhysRevLett.101.067204
- M. Amami, S. Smari, K. Tayeb, P. Strobel and A. Ben Salah, “Cationic Doping Effect on the Structural, Magnetic and Spectroscopic Properties of Delafossite Oxides CuCr1−x(Sc,Mg)xO2,” Journal of Material Chemistry and Physics, Vol. 128, 2011, p. 298.
- G. Williamson and W. H. Hall, “X-Ray Line Broadening from Filed Aluminium and Wolfram,” Acta Metallurgica, Vol. 1, No. 1, 1953, pp. 22-31. doi:10.1016/0001-6160(53)90006-6
- R. Nagarajan, N. Duan, M. K. Jayaraj, J. Li, K. A. Vanaja, A. Yokochi, A. Draeseke, J. Tate and A. W. Sleight, “pType Conductivity in the Delafossite Structure,” International Journal of Inorganic Materials, Vol. 3, No. 3, 2001, pp. 265-270.
- R. Shannon, D. Rogers and C. Prewitt, “Chemistry of Noble Metal Oxides. I. Syntheses and Properties of ABO2 Delafossite Compounds,” Inorganic Chemistry, Vol. 10, No. 4, 1971, pp. 713-718. doi:10.1021/ic50098a011
- L. Vegard, “Lattice Fluctuations in Solid Solution Formation by Precipitation of Solutions,” Journal for Physics A, Vol. 43, No. 5-6, 1927, pp. 299-308. doi:10.1007/BF01397444
- C. Prewitt, R. Shannon and D. Rogers, “Chemistry of Noble Metal Oxides. II. Crystal Structures of Platinum Cobalt Dioxide, Palladium Cobalt Dioxide, Coppper Iron Dioxide and Silver Iron Dioxide,” Inorganic Chemistry, Vol. 10, No. 4, 1971, pp. 719-723. doi:10.1021/ic50098a012
- J. Tate, M. Jayaraj, A. Draeseke, T. Ulbrich, A. Sleight, K. Vanaja, R. Nagarajan, J. Wagner and R. Hoffman, “p-Type Oxides for Use in Transparent Diodes,” Thin Solid Films, Vol. 411, No. 1, 2002, pp. 119-124. doi:10.1016/S0040-6090(02)00199-2
- M. Amami, C. V. Colin, P. Strobel and A. B. Salah, “AlDoping Effect on the Structural and Physical Properties of Delafossite-Type Oxide CuCrO2,” Physica B: Condensed Matter, Vol. 406, No. 11, 2011, pp. 2182-2185. doi:10.1016/j.physb.2011.03.027
- O. Garlea, C. Darie, C. Bougerol, O. Isnard and P. Bordet, “Structure of LaCuO2.66: An Oxidized Delafossite Compound Containing Hole-Doped Kagome Planes of Cu2+ Cations,” Journal of Solid State Sciences, Vol. 5, No. 8, 2003, pp. 1095-1104. doi:10.1016/S1293-2558(03)00145-6
- L. Da, F. Xiaodong, D. Weiwei, D. Zanhong, T. Ruhua, Z. Shu, J. Wang, T. Wang, Y. Zhao and X. Zhu, “Magnetic and Electrical Properties of p-Type Mn-Doped CuCrO2 Semiconductors,” Journal of Physics D: Applied Physics, Vol. 42, No. 5, 2009, p. 55009. doi:10.1088/0022-3727/42/5/055009
- J. Pellicer-Porres, A. Segura, Ch. Ferrer-Roca, D. Martinez-Garcia, J. A. Sans and E. Martinez, “Structural Evolution of the CuGaO2 Delafossite under High Pressure,” Physical Review B, Vol. 69, No. 2, 2004, p. 24109. doi:10.1103/PhysRevB.69.024109
- J. Pellicer-Porres, A. Segura and E. Martinez, “Vibrational Properties of Delafossite CuGaO2 at Ambient and High Pressures,” Physical Review B, Vol. 72, 2005, p. 064301. doi:10.1103/PhysRevB.72.064301
- J. Pellicer-Porres, D. Martinez-Garcia, A. Segura, P. Rodriguez-Hernandez, A. Munoz, J. C. Chervin, N. Garro and D. Kim, “Pressure and Temperature Dependence of the Lattice Dynamics of CuAlO2 Investigated by Raman Scattering Experiments and ab Initio Calculations,” Physical Review B, Vol. 74, No. 18, 2006, pp. 184301- 184309. doi:10.1103/PhysRevB.74.184301
- J. E. Maslar, W. S. Hurst, T. A. Vanderah and I. Levin, “The Raman Spectra of Cr3O8 and Cr2O5,” Journal of Raman Spectroscopy, Vol. 32, No. 3, 2001, pp. 201-206. doi:10.1002/jrs.687
- H. Kadoeaki, H. Kikuchi and Y. Ajiro, “Neutron Powder Diffraction Study of the Two-Dimensional Triangular Lattice Antiferromagnet CuCrO2,” Journal of Physics: Condensed Matter, Vol. 2, No. 19, 1990, p. 4485. doi:10.1088/0953-8984/2/19/014
- F. Jlaiel, M. Amami, N. Boudjada, P. Strobel and A. B. Salah, “Metal Transition Doping Effect on the Structural and Physical Properties of Delafossite-Type Oxide CuCrO2,” Journal of Alloys and Compounds, Vol. 509, No. 29, 2011, pp. 7784-7788. doi:10.1016/j.jallcom.2011.04.153
NOTES
*Corresponding author.

