Journal of Crystallization Process and Technology
Vol.05 No.02(2015), Article ID:55626,11 pages
10.4236/jcpt.2015.52005
Determination of the Metastable Zone Width, Nucleation Kinetics, Structural and Optical Properties of KCl Doped KAP Crystal
M. A. Rahman1*, M. M. Rahman2
1Department of Basic Sciences and Humanities (Physics), University of Asia Pacific, Dhaka, Bangladesh
2Department of physics, Dhaka University, Dhaka, Bangladesh
Email: *anis.phyuap@yahoo.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 February 2015; accepted 10 April 2015; published 14 April 2015
ABSTRACT
Slow evaporation method was used to grow pure and KCl (10 mol%) doped KAP single crystal. The solubility and metastable zone width of aqueous solutions of pure and KCl (10 mol%) doped KAP crystal were evaluated to analyze the crystallization process. Measuring the induction period τ, the critical nucleation parameters like interfacial energy (σ), energy of formation of the critical nucleus (∆G*) were determined using the classical theory of nucleation. The structural properties and optical constants of the grown crystals have been put to test and observed that the addition of KCl results in an enhancement of properties of the crystal. Grown crystals were characterized by powder X-ray diffraction. FTIR spectra confirmed the presence of KCl in pure KAP crystal. UV- Visible spectroscopic studies revealed that addition of KCl in pure KAP crystal increased transparency from 75% to 80%. The analysis of the optical absorption data revealed the presence of both indirect and direct transitions and both of these band gaps increased with the addition of KCl. The transmittance data was analyzed to calculate the refractive index, oscillator energy, dispersion energy, electric susceptibility, zero-frequency dielectric constant and both the real and imaginary parts of the dielectric permittivity as a function of photon energy. The moments of ε(E) were also determined. The dispersion i.e. spectral dependence of the refractive index was discussed according to the single-effective oscillator model proposed by Wemple and DiDomenico.
Keywords:
Single Crystal, Growth from Solution, Metastable Zone Width, FTIR, UV-Visible Spectroscopy, Optical Constants

1. Introduction
Growth of potassium acid phthalate (KAP) crystal of high purity has become an important field of research in a variety of areas. KAP exhibits orthorhombic lattice structure with four molecules per unit cell and the unit cell parameters are a = 6.320 Å, b = 12.343 Å, c = 5.784 Å. On the other hand, in production of optical windows, single crystal of KCl with wide band gap (~8 eV) is widely used [1] . Moreover, there is application for optical components in wide spectrum band from the ultraviolet to the infrared, because of its transparency over the entire range of wavelengths. Though potassium chloride has a low refractive index, its damage threshold is high. KCl lattice is fcc; the basis of the crystal consists of one K atom and one Cl atom separated by one half the body diagonal of a unit cube. The structure of KCl crystal is cubic with lattice parameters of a = b = c = 6.29170 Å. There are four units of KCl in each unit cube [2] .
An effort to investigate the nucleation kinetics and optical constants of KCl doped (10 mol%) KAP crystal is done. Since nucleation is affected by width of the metastable zone, it is essential to measure it for designing products by crystallization processes. It is possible to obtain optimum crystallization processes by tuning the metastable zone width and actual operation point of the crystallizer within this zone [3] . The findings are expected to provide valuable information for designing optoelectronics devices intended for NLO applications.
2. Experimental Details
2.1. Crystal Growth
Analytical reagent grade (AR) and doubled distilled water were used for growing the crystals. At first good quality seed crystals were selected. The seeds were obtained by spontaneous nucleation technique. Later bulk size crystals were harvested by slow evaporation method at room temperature in a span of 60 - 80 days. The as- grown crystals are shown in Figure 1.
2.2. Determination of the Solubility and Metastable Zone Width
In order to observe the dependence on temperature, the solubility of KCl (10 mol%) doped KAP solutions was determined for five different temperatures, namely, 30˚C, 35˚C, 40˚C, 45˚C, and 50˚C. The measurements were carried out in a constant temperature water bath (CTB) with cryostat facility. In our study, polythermal method was used to determine the metastable zone width of pure and KCl (10 mol%) doped KAP solutions [4] [5] . First of all the solutions were kept in a CTB with cryostat facility. Using a magnetic stirrer the solutions were stirred continuously for a period of 7 hours and it was slowly cooled at a rate of 3 K/h. At the appearance of the first crystal, the temperature was noted there and then. The metastable zone width of the solution was measured as the change in saturation and nucleation temperature [5] . The method was replicated for rest of the saturation temperatures; 35˚C, 40˚C, 45˚C, and 50˚C, and the respective metastable zone widths were obtained.
2.3. Density of the Crystal
The density of the crystal was measured experimentally by the floatation method at room temperature (30˚C) using the following expression
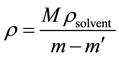 (1)
(1)
where m, m' and ρsolvent are the mass of crystal sample in the air, the mass when the crystal sample was immersed in CCl4 and the density of solvent (CCl4) at measured temperature, respectively. The density of the doped crystal was found to be 1.808 g/cm3.
2.4. Determination of Induction Period
The induction period τ gives the insight about the process that leads growth from critical nuclei to detectable crystals and is determined experimentally by isothermal method [5] [6] . In order to get the required degree of supersaturation, at first the required amount of KAP (with and without KCl) was dissolved in the solvent and

Figure 1. Photograph of the as-grown crystals: (a) Pure KAP crystal and (b) KCl (10 mol%) doped KAP crystal.
then the solution was cooled to the saturation temperature (30◦C). At this stage the solution became supersaturated to the particular level of supersaturation. Once the nucleation occurred, the nucleus grew quickly and formed a bright sparkling speck. The induction period was taken as the difference of the time of observation of the sparkling particle and the time at which the solution reached the saturation temperature [5] . Experiments were repeated to get the following degrees of supersaturation (C/C*); 1.03, 1.06, 1.09, 1.13 and 1.16, (C and C* are the concentration of solute in supersaturated solution and the saturated concentration, respectively).
2.5. XRD Analysis
The crystals were ground using an agate mortar and pestle. The powder X-ray diffraction analysis on pure and KCl doped KAP crystal was recorded using CuKα radiation and has been recorded up to 2θ = 85˚.
2.6. FT-IR Analysis
By using KBr pellet technique, the FT-IR spectrum of the crystal was recorded at room temperature to identify the functional groups. All the spectra were recorded in transmittance (%) mode in the region of 4000 to 400 cm−1. The characteristic vibrational frequencies were assigned and compared with the doped sample.
2.7. UV-VIS Spectral Analysis
The crystals were polished without any antireflection coating and the optical transmission spectrum of 2 mm thick crystal was recorded in the wavelength range of 250 - 750 nm at room temperature in order to derive the absorption coefficient, refractive index and other important optical constants such as oscillator energy, dispersion energy, oscillator strength and zero-frequency refractive index, etc.
3. Results and Discussions
3.1. Solubility and Metastable Zone Width
It is observed from Figure 2(a) that the metastable zone width has increased due to the addition of KCl (10 mol%). Trivalent metals like Cr3+, Fe3+ and Al3+ can significantly affect the growth of the crystals. Even after repeated recrystallization these impurities cannot be completely removed and doping can do what recrystallization cannot do, i.e. it can reduce the effect of these impurities. In order to enhance the metastable zone width as well as to achieve optimum growth rate of the crystals, KCl is incorporated in the solution. As it is believed that the harmful effect of the metal ion impurities can be moderated by adding KCl [7] .
3.2. Nucleation Kinetics
The interfacial energy σ takes on a prominent part in the nucleation of crystals [8] . This parameter has been cal-

Figure 2. (a) Solubility and metastable zone width and (b) ln t versus 1/(ln S)2 for pure and KCl added KAP solution.
culated from induction period. The equation of nucleation rate relating induction period can be written as [9]
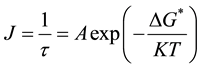
or 
or 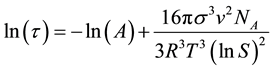 (2)
(2)
where τ is the induction period of the solution at temperature T, v is the molar crystal volume and A is constant. S is the supersaturation ratio (S = C/C*). At constant temperature, a straight ahead relationship is noticed between lnτ and 1/(lnS)2 (Figure 2(b)), due to independence of lnA on temperature. Many researchers considered two different straight lines: one standing for homogeneous nucleation and the other heterogeneous nucleation [10] . The interfacial energy σ (Figure 3(a)) has been determined using the following expression [11]
 (3)
(3)
where m is the slope evaluated from the straight line fit for lnτ against 1/(lnS)2, R is the gas constant, and NA is Avogadro’s number. The energy of formation of a critical nucleus (Figure 3(b)) has been evaluated using the following equation
 (4)
(4)
3.3. X-Ray Diffraction Analysis
The grown crystal was put through the powder XRD which was shown in Figure 4. The unit cell parameters are given in Table 1. The well-defined Bragg’s peaks at specific 2θ angles give the evidence of high crystallinity of the crystal. It is observed from the XRD data that there is a slight change in the peak position and unit cell parameters which indicates that KCl might have entered into KAP molecular structure.

Figure 3. (a) Interfacial energy and (b) Energy ΔG* versus super saturation ratio S of pure and KCl added KAP solution.
Figure 4. Powder X-ray diffraction of (a) pure KAP and (b) KCl (10 mol%) doped KAP crystal.
3.4. FTIR Spectra
Figure 5 shows the FTIR spectra of the pure and KCl (10 mol%) doped KAP crystal. The peak assignment is given in Table 2. The data indicate shifting of symmetrical C=O stretching of KAP to higher energy for KCl doping. This budge to higher energy indicates interaction of KAP with KCl [12] . The characteristic C-COO stretching and C=C-C at 1285.58 and 581.55 cm−1 are shifted to 1286.54 and 582.51 cm−1, indicating substitution. The asymmetric stretching vibration of the carboxylate ion is shifted to lower energy (1562.37 cm−1) compared with pure KAP (1572.01 cm−1).
3.5. Optical Studies
The UV-VIS transmittance spectra and reflectance curve (inset) of pure and KCl (10 mol%) doped KAP crystals are shown in Figure 6. A cut off wavelength is noticed near about 240 nm. There is no striking absorption in the entire region of the spectrum. The investigation of the optical absorption coefficient on the photon energy has
Table 1. Unit cell parameters of pure and KCl doped KAP crystals.
Table 2. Vibrational frequencies obtained for pure and doped KAP crystals through FTIR studies.
Figure 5. FTIR spectrum for (a) pure KAP and (b) KCl (10 mol%) doped KAP crystals.

Figure 6. UV-VIS spectra and reflectance curve (inset) of (a) Pure KAP and (b) KCl (10 mol%) doped KAP crystals.
become a fashionable way to interpret the band structure and nature of transition of electrons. The optical energy gap Eg can be expressed with respect to the incident pthoton energy hn by Equation (5) [13] ,

where a is the optical absorption coefficient, A is a constant, hν = photon energy, Eg = Energy gap, p is thought to as 2 or 1/2 for a indirect or direct allowed transitions, respectively. The plot of absorption coefficient a on photon energy hn is given in Figure 7. Direct and indirect band gap Egd and Egi are evaluated by the extrapolations of the linear part down to 

The rise of the band gap due to doping may be thought of as falling off irregularity and defects in the crystal which is in fact viewed as rise of an electric field by an electrically charged particles within the crystal [15] . The extinction coefficient (K) can be written as

where λ is the wavelength of the incident radiation.

Figure 7. (a) (αhν)1/2and (b) (αhν)2 as a function of photon energy for pure and KCl (10 mol%) doped KAP crystals.
Table 3. Optical parameters of pure and KCl (10 mol%) doped KAP crystals.
crystal structure. Atoms easily polarizable (i.e. electron are easily displaced) give rise to a high refractive index. The equations relating transmittance (T), reflectance (R) and refractive index (n) can be expressed with the following equations (considering T + R = 1) [16] .
Hence,


The complex dielectric constant εc can be expressed with real (εr) and imaginary (εi) parts of dielectric constant as




where c is the velocity of light and n is the refractive index. The electrical conductivity can be written as [16]

Non linear optical (NLO) property is expected for the crystal because Figure 8 reveals the lower value of complex dielectric constant along the transmission range which in turn indicates induced polarization. Lower electrical conductivity at higher photon energy (Figure 9(a)) specifies the dielectric nature of the material. On the other hand, the higher value of optical conductivity at higher photon energy (Figure 9(b)) brings to light superior conversion capability for second harmonics generation devices.
The electrical susceptibility (χc) can be assessed by the relation [15]


From Figure 10(a), it is clear that electrical susceptibility is larger than 1 and the material is polarizable if the light is made highly intense.

Figure 8. (a) Real part (er) and (b) Imaginary part (ei) of dielectric constant as a function of photon energy for pure and KCl (10 mol%) doped KAP crystals.

Figure 9. Relations of (a) Electrical conductivity (σe) and (b) Optical conductivity (σo) with photon energy for pure and KCl (10 mol%) doped KAP crystals.

Figure 10. (a) Electrical susceptibility and (b) Refractive index as a function of wavelength for pure and KCl (10 mol%) doped KAP crystals.
Wemple and Di Domenico made use of the single effective oscillator equation and investigated refractive index data lower to the interband absorption edge. The relation between the refractive index and photon energy can be expressed by the equation [17]

where Eso and Ed are the single oscillator and the dispersion energy, respectively. Figure 10(b) plots the change of the refractive index with wavelength. In Figure 11(a), the oscillator parameters are figured out from (n2 − 1)−1 versus (hν)2 plot by measuring the slope and intersection of the straight line with y-axis. The above-men- tioned model establishes a connection between the single oscillator parameters Eso and Ed and imaginary part εi of the complex dielectric constant. The M−1 and M−3 moments of the ε(E) optical spectrum can be formulated as the following expression


Figure 11. (a) 1/(n2 − 1) as a function of (hn)2and (b) 1/(n2-1) as a function of l−2 for pure and KCl (10 mol%) doped KAP crystals.

The zero-frequency refractive index n0 can be achieved by the expression

The zero-frequency dielectric constant is obtained by using the relation

where 

where

4. Conclusion
Pure and KCl doped KAP crystals were grown by adopting slow evaporation method. The solubility varied proportionately with temperature. Incorporation of KCl resulted in increase of the metastable zone width and interfacial energy with respect to undoped solution. The possible reason of this enhancement might be considered as opposition in chemical activity faced by the metal ions in the mother solution. XRD analysis indicated incorporation of foreign atoms into the KAP crystal matrix. The UV-VIS spectra analysis showed that the transmission capability got better as well as revealed the coexistence of indirect and direct transitions in KCl doped KAP crystals. Optical constants such as the dispersion energy, oscillator strength, oscillator energy and zero-frequ- ency refractive index were evaluated by making use of the Wemple-Di Domenico single-effective-oscillator model and observed to change considerably due to KCl doping.
Acknowledgements
Authors are grateful to Dr. Abdul Gafur and Dr. Dilip Kumar Saha for their kind permission to perform FTIR and XRD study.
References
- Samavat, F., Ali, E.H., Solgi, S. and Taravati Ahmad, P. (2012) KCl Single Crystals Growth with Mn, Ag and In Impurities by Czochralski Method and Study of Impurities Influence on Their Properties. Open Journal of Physical Chemistry, 2, 185-188. http://dx.doi.org/10.4236/ojpc.2012.23025
- Joseph, J., Mathew, V. and Abraham, K. E. (2008) Electro-Optical, Optical and Structural Properties of Mn Doped Potassium Chloride Crystals Prepared by a Mini Melt Growth Setup. Journal of Physics, 35, 198-212.
- Ulrich, J. and Strege, C. (2002) Some Aspects of the Importance of Metastable Zone Width and Nucleation in Industrial Crystallizers. Journal of Crystal Growth, 237-239, 2130-2135. http://dx.doi.org/10.1016/S0022-0248(01)02284-9
- Tilley, R. (2006) Crystals and Crystal Structure. John Wiley & Sons Ltd., England.
- Rahman, A. and Podder, J. (2010) Effect of EDTA on the Growth Kinetics and Structural and Optical Properties of KDP Crystal. International Journal of Optics, 2010, Article ID: 978763. http://dx.doi.org/10.1155/2010/978763
- Zaitseva, N.P., Rashkovich, L.N. and Bogatyreva, S.V. (1995) Stability of KH2PO4 and K(H,D)2PO4 Solutions at Fast Crystal Growth Rates. Journal of Crystal Growth, 148, 276-282. http://dx.doi.org/10.1016/0022-0248(94)00606-7
- Podder, J. (2002) The Study of Impurities Effect on the Growth and Nucleation Kinetics of Potassium Dihydrogen Phosphate. Journal of Crystal Growth, 237-239, 70-75. http://dx.doi.org/10.1016/S0022-0248(01)01854-1
- Rahman, A. and Podder, J. (2012) Effect of EDTA on the Metastable Zone Width and Growth Kinetics of ADP Crystal. Indian Journal of Physics, 86, 15-21. http://dx.doi.org/10.1007/s12648-012-0003-8
- Jothi Mani, R. and Selvarajan, P. (2014) Nucleation Kinetics, Growth, Nlo Studies, Hardness Parameters and Etching Analysis of Phosphoric Acid Added L-Alanine Single Crystals (Pla). International Journal of ChemTech Research, 6, 4702-4708. http://sphinxsai.com/2014/ch_vol6_no11/3/%284702-4708%29N14.pdf
- Kanagasekaran, T., Gunasekaran, M., Srinivasan, P., Jayaraman, D., Gopalakrishnan, R. and Ramasamy, P. (2005) Studies on Growth, Induction Period, Interfacial Energy and Metastable Zone Width of m-Nitroaniline. Crystal Research and Technology, 40, 1128-1133. http://dx.doi.org/10.1002/crat.200410504
- Uthayarani, K., Sankar, R. and Shashidharan Nair, C.K. (2008) Growth, Spectral and Thermal Properties of KAP Single Crystals in the Presence of DL-Alanine and L-Methionine Amino Acid Dopants. Crystal Research and Technology, 43, 733-739. http://dx.doi.org/10.1002/crat.200711091
- Thendral, V., Thayumanavan, A., Pasupathi, G. and Marudhu, G. (2013) Enhancement of Optical, Thermal and Mechanical Properties of Kap Crystals by Magnesium Doping. IOSR Journal of Applied Physics, 3, 62-68. http://dx.doi.org/10.9790/4861-0336268
- Fox, M. (2001) Condensed Matter Physics, Oxford Master Series, 64.
- Kusuma, H.H., Saidin, M.K. and Ibrahim, Z. (2009) Optical Properties of Ti:Al2O3 Single Crystal. Jabatan Fizk UTM, 4, 42-49. http://eprints.utm.my/7312/1/HamdanHadiKusuma2009_OpticalPropertiesof.pdf
- Vasudevan, P., Sankar, S. and Jayaraman, D. (2013) Synthesis, Optical and Electrical Studies of Nonlinear Optical Crystal: L-Arginine Semi-Oxalate. Bulletin of the Korean Chemical Society, 34, 128-132. http://journal.kcsnet.or.kr/main/j_search/j_download.htm?code=B130123 http://dx.doi.org/10.5012/bkcs.2013.34.1.128
- Victor Antony Raj, M., Anand, D.P. and Madhavan, J. (2013) Linear and Non Linear Optical Properties of L-Alani- nium Malate (LAM) Single Crystal an Efficient Organic NLO Material. Sciencia Acta Xaveriana, 4, 41-50.
- Wemple, S.H. (1973) Refractive-Index Behavior of Amorphous Semiconductors and Glasses. Physical Review B, 7, 3767. http://dx.doi.org/10.1103/PhysRevB.7.3767
- Tanaka, K. (1980) Optical Properties and Photoinduced Changes in Amorphous AsxS100-x. Films. Thin Solid Films, 66, 271-279. http://dx.doi.org/10.1016/0040-6090(80)90381-8
- Yakuphanoglu, F., Cukurovali, A. and Yilmaz, I. (2004) Determination and Analysis of the Dispersive Optical Constants of Some Organic Thin Films. Physica B: Condensed Matter, 351, 53-58. http://dx.doi.org/10.1016/j.physb.2004.05.010
NOTES
*Corresponding author.















