About Multichannel Speech Signal Extraction and Separation Techniques

Adel Hidri, Souad Meddeb, Hamid Amiri

Signal Image and Technology of Information Laboratory, National Engineering School of Tunis, Tunis, Tunisia.

DOI: 10.4236/jsip.2012.32032                

Abstract

The extraction of a desired speech signal from a noisy environment has become a challenging issue. In the recent years, the scientific community has particularly focused on multichannel techniques which are dealt with in this review. In fact, this study tries to classify these multichannel techniques into three main ones: Beamforming, Independent Component Analysis (ICA) and Time Frequency (T-F) masking. This paper also highlights their advantages and drawbacks. However these previously mentioned techniques could not afford satisfactory results. This fact leads to the idea that a combination of those techniques, which is depicted along this study, may probably provide more efficient results. Indeed, giving the fact that those approaches are still be considered as being not totally efficient, has led us to review these mentioned above in the hope that further researches will provide this domain with suitable innovations.

Keywords

Beamforming; ICA; T-F Masking; BSS; Multichannel; Speech Separation; Microphone Array

1. Introduction

Most audio signals result from the mixing of several sound sources. In many applications, there is a need to separate the multiple sources or extract a source of interest while reducing undesired interfering signals and noise. The estimated signals may then be either directly listened to or further processed, giving rise to a wide range of applications such as hearing aids, human computer interaction, surveillance, and hands-free telephony [1].

The extraction of a desired speech signal from a mixture of multiple signals is classically referred to as the “cocktail party problem” [2,3], where different conversations occur simultaneously and independently of each other.

The human auditory system shows a remarkable ability to segregate only one conversation in a highly noisy environment, such as in a cocktail party environment. However, it remains extremely challenging for machines to replicate even part of such functionalities. Despite being studied for decades, the cocktail party problem remains a scientific challenge that demands further research efforts [4].

As highlighted in some recent works [5], using a single channel is not possible to improve both intelligibility and quality of the recovered signal at the same time. Quality can be improved at the expense of sacrificing intelligibility. A way to overcome this limitation is to add some spatial information to the time/frequency information available in the single channel case. Actually, this additional information could be obtained by using two or more channel of noisy speech named multichannel.

Three techniques of Multi Channel Speech Signal Separation and Extraction (MCSSE) can be defined. The first two techniques are designed to determined and overdetermined mixtures (when the number of sources is smaller than or equal to the number of mixtures) and the third is designed to underdetermined mixtures (when the number of sources is larger than the number of mixtures). The former is based on two famous approaches, the Blind Source Separation (BSS) techniques [5-7] and the Beamforming techniques [8-10].

BSS aims at separating all the involved sources, by exploiting their independent statistical properties, regardless their attribution to the desired or interfering sources.

On the other hand, the Beamforming techniques, concentrate on enhancing the sum of the desired sources while treating all other signals as interfering sources. While the latter uses the knowledge of speech signal properties for separation.

One popular approach to sparsity based separation is T-F masking [11-13]. This approach is a special case of non-linear time-varying filtering that estimates the desired source from a mixture signal by applying a T-F mask that attenuates T-F points associated with interfering signals while preserving T-F points where the signal of interest is dominant.

In the last years, the researches in this area based their approaches on combination techniques as ICA and binary T-F masking [14], Beamforming and a time frequency binary mask [15].

This paper is concerned with a survey of the main ideas in the area of speech separation and extraction from a multiple microphones.

The following sections of this paper are organized as follows: in Section 2, the problem of speech separation and extraction is formulated. In Section 3, we describe some of the most techniques which have been used in MCSSE systems, such as Beamforming, ICA and T-F masking techniques. Section 4 brings to the surface the most recent methods for MCSSE systems, where combined techniques, seen previously, are used. In Section 5, the presented methods will be discussed by giving some of their advantages and limits. Finally, Section 6 gives a synopsis of the whole paper and conveys some futures works.

2. Problem Formulation

There are many scenarios where audio mixtures can be obtained. This results in different characteristics of the sources and the mixing process that can be exploited by the separation methods. The observed spatial properties of audio signals depend on the spatial distribution of a sound source, the sound scene acoustics, the distance between the source and the microphones, and the directivity of the microphones.

In general, the problem of MCSSE is stated to be the process of estimating the signals from N unobserved sources, given from M microphones, which arises when the signals from the N unobserved sources are linearly mixed together as presented in Figure 1.

The signal recorded at the j^th microphone can be modeled as:

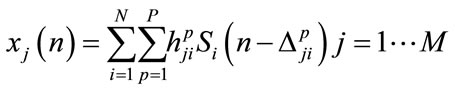(1)

where and are the source and mixture signals respectively, h_ji is a P-point Room Impulse Response (RIR) from source i to microphone j, P is the number of paths between each source-microphone pair and is the delay of the p^th path from source j to microphone i [9-14]. This model is the most natural mixing model, encountered in live recordings called echoic mixtures.

In free-reverberation environments (p = 1), the samples of each source signal can arrive at the microphones only from the line of sight path, and the attenuation and delay of source i would be determined by the physical position of the source relative to the microphones. This model, called anechoic mixing, is described by the following equation obtained from the previous equation:

Figure 1. Multichannel problem formulation.

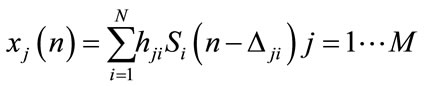(2)

The instantaneous mixing model is a specific case of the anechoic mixing model where the samples of each source arrive at the microphones at the same time with differing attenuations, each element of the mixing matrix is a scalar that represents the amplitude scaling between source i and microphone j. From the Equation (2), instantaneous mixing model can be expressed as:

(3)

3. MCSSE Techniques

3.1. Beamforming Technique

Beamforming is a class of algorithms for multichannel signal processing. The term Beamforming refers to the design of a spatio-temporal filter which operates on the outputs of the microphone array [8]. This spatial filter can be expressed in terms of dependence upon angle and frequency. Beamforming is accomplished by filtering the microphone signals and combining the outputs to extract (by constructive combining) the desired signal and reject (by destructive combining) interfering signals according to their spatial location [9].

Beamforming for broadband signals like speech can, in general, be performed in the time domain or frequency domain. In time domain Beamforming, a Finite Impulse Response (FIR) filter is applied to each microphone signal, and the filter outputs combined to form the Beamformer output. Beamforming can be performed by computing multichannel filters whose output is an estimate of the desired source signal as shown in Figure 2.

The output can be expressed as:

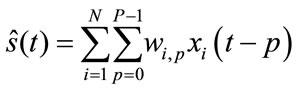(4)

where P – 1 is the number of delays in each of the N filters.

Figure 2. MCSSE with Beamforming technique.

In frequency domain Beamforming, the microphone signal is separated into narrowband frequency bins using a Short-Time Fourier Transform (STFT), and the data in each frequency bin is processed separately.

Beamforming techniques can be broadly classified as being either data-independent or data-dependent. Data independent or deterministic Beamformers are so named because their filters do not depend on the microphone signals and are chosen to approximate a desired response. Conversely, data-dependent or statistically optimum Beamforming techniques are been so called because their filters are based on the statistics of the arriving data to optimize some function that makes the Beamformer optimum in some sense.

3.1.1. Deterministic Beamformer

The filters in a deterministic Beamformer do not depend on the microphone signals and are chosen to approximate a desired response. For example, we may wish to receive any signal arriving from a certain direction, in which case the desired response is unity over at that direction. As another example, we may know that there is interference operating at a certain frequency and arriving from a certain direction, in which case the desired response at that frequency and direction is zero. The simplest deterministic Beamforming technique is delay-and-sum Beamforming, where the signals at the microphones are delayed and then summed in order to combine the signal arriving from the direction of the desired source coherently, expecting that the interference components arriving from off the desired direction cancel to a certain extent by destructive combining. The delay-and-sum Beamformer as shown in Figure 3 is simple in its implementation and provides easy steering of the beam towards the desired source. Assuming that the broadband signal can be decomposed into narrowband frequency bins, the delays can be approximated by phase shifts in each frequency band.

The performance of the delay-and-sum Beamformer in reverberant environments is often insufficient. A more general processing model is the filter-and-sum Beamformer as shown in Figure 4 where, before summation, each microphone signal is filtered with FIR filters of order M. This structure, designed for multipath environments namely reverberant enclosures, replaces the simpler delay compensator with a matched filter. It is one of the simplest Beamforming techniquesbut still gives a very good performance.

Figure 3. Delay-and-sum Beamforming.

Figure 4. Filter and sum Beamforming.

As it has been shown that the deterministic Beamformer is far from being fully manipulated independently from the microphone signals, the statistically optimal Beamformer is tightly linked and tied to the statistical properties of the received signals.

3.1.2. Statistically Optimum Beamformer

Statistically optimal Beamformers are designed basing on the statistical properties of the desired and interference signals. In this category, the filters designs are based on the statistics of the arriving data to optimize some function that makes the Beamformer optimum in some sense. Several criteria can be applied in the design of the Beamformer, e.g., maximum signal-to-noise ratio (MSNR), minimum mean-squared error (MMSE), minimum variance distortionless response (MVDR) and linear constraint minimum variance (LCMV). A summary of several design criteria can be found in [10]. In general, they aim at enhancing the desired signals, while rejecting the interfering signals.

Figure 5 depicts the block diagram of Frost Beamformer or an adaptive filter-and-sum Beamformer as proposed in [16], where the filter coefficients are adapted using a constrained version of the Least Mean-Square (LMS) algorithm. The LMS is used to minimize the noise power at the output while maintaining a constraint

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	M. Brandstein and D. Ward, “Microphone Arrays: Signal Processing Techniques and Applications,” Digital Signal Processing, 2001, Springer.
[2]	C. Cherry: “Some Experiments on the Recognition of Speech, with One and with Two Ears,” Journal of the Acoustical Society of America, Vol. 25, No. 5, 1953, pp. 975–979. doi:10.1121/1.1907229
[3]	S. Haykin and Z. Chen, “The Cocktail Party Problem,” Journals of Neural Computation, Vol. 17, No. 9, 2005, pp. 1875-1902. doi:10.1162/0899766054322964
[4]	D. L. Wang and G. J. Brown, “Computational Auditory Scene Analysis: Principles Algorithms and Applications,” Wiley, New York, 2006. 10.1109/TNN.2007.913988
[5]	J. Benesty, S. Makino and J. Chen, “Speech Enhancement,” Signal and Communication Technology, Springer, Berlin, 2005.
[6]	S. Douglas and M. Gupta, “Convolutive Blind Source Separation for Audio Signals,” Blind Speech Separation, Springer, Berlin, 2007. doi:10.1007/978-1-4020-6479-1_1
[7]	H. Sawada, S. Araki and S. Makino “Frequency-Domain Blind Source Separation,” Blind Speech Separation, Springer, Berlin, 2007. doi:10.1007/3-540-27489-8_13
[8]	S. Markovich, S. Gannot and I. Cohen, “Multichannel Eigen Space Beamforming in a Reverberant Noisy Environment with Multiple Interfering Speech Signals,” IEEE Transactions on Audio, Speech, and Language Processing, Vol. 17, No. 6, 2009, pp. 1071-1086. doi:10.1109/TASL.2009.2016395
[9]	M. A. Dmour and M. Davies “A New Framework for Underdetermined Speech Extraction Using Mixture of Beamformers,” IEEE Transactions on Audio, Speech, and Language Processing, Vol. 19, No. 3, 2011, pp. 445-457. doi:10.1109/TASL.2010.2049514
[10]	J. Benesty, J. Chen and Y. Huang, “Conventional Beamforming Techniques,” Microphone Array Signal Processing, Springer, Berlin, 2008. doi:10.1121/1.3124775
[11]	V. G. Reju, S. N. Koh and I. Y. Soon, “Underdetermined Convolutive Blind Source Separation via Time-Frequency Masking,” IEEE Transactions on Audio, Speech, and Language Processing, Vol. 18, No. 1, 2010, pp. 101-116. doi:10.1109/TASL.2009.2024380
[12]	O. Yilmaz and S. Rickard, “Blind Separation of Speech Mixtures via Time-Frequency Masking,” IEEE Transactions on Signal Processing, Vol. 52, 2004, pp. 1830-1847. doi:10.1109/TSP.2004.828896
[13]	J. Freudenberger and S. Stenzel, “Time-Frequency Masking for Convolutive and Noisy Mixtures,” Workshop on Hands-Free Speech Communication and Microphone Arrays, 2011, pp. 104-108. doi:10.1109/HSCMA.2011.5942374
[14]	T. Jan, W. Wang and D. L. Wang, “A Multistage Approach to Blind Separation of Convolutive Speech Mixtures,” Speech Communication, Vol. 53, 2011, pp. 524-539. doi:10.1016/j.specom.2011.01.002
[15]	J. Cermak, S. Araki, H. Sawada and S. Makino, “Blind Speech Separation by Combining Beamformers and a Time Frequency Binary Mask,” IEEE International Conference on Acoustics, Speech and Signal Processing, Honolulu, 2007, pp. I-145-I-148.
[16]	O. Frost, “An Algorithm for Linearly Constrained Adaptive Array Processing,” Proceedings of the IEEE, Vol. 60, No. 8, 1972, pp. 926-935.
[17]	E. A. P. Habets, J. Benesty, I. Cohen, S. Gannot and J. Dmochowski, “New Insights into the MVDR Beamformer in Room Acoustics,” IEEE Transactions on Audio, Speech, and Language Processing, 2010, pp. 158-170. doi:10.1109/TASL.2009.2024731
[18]	L. Griffiths and C. Jim, “An Alternative Approach to Linearly Constrained Adaptive Beamforming,” IEEE Transactions on Antennas and Propagation, Vol. 30, No. 1, 1982, pp. 27-34. doi:10.1109/TAP.1982.1142739
[19]	S. Gannot and I. Cohen “Adaptive Beamforming and Post filtering,” Speech Processing, Springer, Berlin, 2007, pp. 199-228.
[20]	A. Spriet, M. Moonen and J. Wouters, “Spatially Pre-Processed Speech Distortion Weighted Multi-Channel Wiener Filtering for Noise Reduction,” Signal Processing, Vol. 84, No. 12, 2004, pp. 2367-2387. doi:10.1016/j.sigpro.2004.07.028
[21]	P. Comon, “Independent Component Analysis, a New Concept,” Signal Processing, Vol. 36, No, 3, 1994, pp. 287-314. doi:10.1016/0165-1684(94)90029-9
[22]	Z. Koldovsky and P. Tichavsky, “Time-Domain Blind Audio Source Separation Using Advanced ICA Methods,” Interspeech, Antwerp Belgium, 2007, pp. 846-849.
[23]	S. Makino, H. Sawada, R. Mukai and S. Araki, “Blind Source Separation of Convolutive Mixtures of Speech in Frequency Domain,” IEICE Transactions on Fundamentals of Electronics Communications and Computer Sciences, No. 7, 2005, pp. 1640-1655. doi:10.1093/ietfec/e88-a.7.1640
[24]	A. Sarmiento, I. Durán-Díaz, S. Cruces and P. Aguilera, “Generalized Method for Solving the Permutation Problem in Frequency-Domain Blind Source Separation of Convolved Speech Signals,” Interspeech, 2011, pp. 565-568.
[25]	R. Mazur and A. Mertins, “A Sparsity Based Criterion for Solving the Permutation Ambiguity in Convolutive Blind Source Separation,” IEEE International Conference on Acoustics, Speech and Signal Processing, Prague Czech Republic, 2011, pp. 1996-1999. doi:10.1109/ICASSP.2011.5946902
[26]	H. Sawada, R. Mukai, S. Araki and S. Makino, “A Robust and Precise Method for Solving the Permutation Problem of Frequency-Domain Blind Source Separation,” IEEE Transactions on Speech and Audio Processing, Vol. 12, No. 5, 2004, pp. 530-538. doi:10.1109/TSA.2004.832994
[27]	M. S. Pedersen, J. Larsen, U. Kjems and L. C. Parra, “A Survey of Convolutive Blind Source Separation Methods,” Handbook on Speech Processing and Speech Communication, Springer, Berlin, 2007.
[28]	S. Rickard, “The DUET Blind Source Separation Algorithm,” Blind Speech Separation, Springer, Berlin, 2007. doi:10.1007/978-1-4020-6479-1_8
[29]	A. Jourjine, S. Rickard and O. Yilmaz, “Blind Separation of Disjoint Orthogonal Signals: Demixing n Sources from 2 Mixtures,” IEEE International Conference on Acoustics, Speech, and Signal Processing, Vol. 5, 2000, pp. 2985-2988. doi:10.1109/ICASSP.2000.861162
[30]	S. Araki, H. Sawada and S. Makino, “K-Means Based Underdetermined Blind Speech Separation,” Blind Speech Separation, Springer, Berlin, 2007. doi:10.1007/978-1-4020-6479-1_9
[31]	R. O. Duda, P. E. Hart and D. G. Stork, “Pattern Classification,” Wiley & Sons Ltd., New York, 2000.
[32]	M. S. Pedersen, D. L. Wang, J. Larsen and U. Kjems “Two-Microphone Separation of Speech Mixtures,” IEEE Transactions on Neural Networks, Vol. 19, No. 3, 2008, pp. 475-492. doi:10.1109/TNN.2007.911740
[33]	D. L. Wang, “On Ideal Binary Mask as the Computational Goal of Auditory Scene Analysis,” Speech Separation by Humans and Machines, Springer, Berlin, 2005, pp. 181-197. doi:10.1007/0-387-22794-6_12
[34]	I. Jafari, R. Togneri and S. Nordholm, “Review of Multi-Channel Source Separation in Realistic Environments,” 13th Australasian International Conference on Speech Science and Technology, Melbourne, 14-16 December 2010, pp. 201-204.
[35]	S. Araki and T. Nakatani, “Hybrid Approach for Multichannel Source Separation Combining Time Frequency Mask with Multi-Channel Wiener Filter,” IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, 22-27 May 2011, pp. 225-228. doi:10.1109/ICASSP.2011.5946381
[36]	L.Wang, H. Ding and F. Yin, “Target Speech Extraction in Cocktail Party by Combining Beamforming and Blind Source Separation,” Journal Acoustics Australia, Vol. 39, No. 2, 2011, pp. 64-68.