Xia Liu, Ruifang Wang, Fabao Gao
School of Mathematical Science, Yangzhou University, Yangzhou, China.
DOI: 10.4236/jamp.2020.83038   PDF    HTML   XML   482 Downloads   1,111 Views   Citations

Abstract

Combined with real engineering, we mainly study the stability of the equilibrium state at the coordinate center of an orthotropic stringer shell system, and the approximate analytic periodic motion is presented around the studied equilibrium state. In addition the rationality of the obtained results is verified by numerical simulation. Furthermore we found that there are actually only four kinds of phase portrait of this type of shell.

Keywords

Stability, Periodic Solution, Stringer Shell, Successor Function

Share and Cite:

1. Introduction

It is generally known that stringer shell plays an indispensable role in the structural design of aircraft, spacecraft, and ships. The studies on nonlinear dynamics of stringer shell have attracted the attention of a large number of researchers (see [1] - [15] and the references therein).

For the case of a cutout in the shell, Palazotto [1] performed a bifurcation and collapse analysis of the stiffened cylindrical shell. In recent years, when the stringer buckles, Gavrilenko and Matsner [2] used the linear and nonlinear theory of the ribbed shell to examine how the stringer shells lose their stability characteristics. Schilling and Mittelstedt [3] derived a clear analytical formula for critical buckling loads by using the Ritz-like principle of minimum potential energy. To illustrate the potential of lightweight optimal designs in terms of structural stability, Khodaygan and Bohlooly [4] conducted a detailed study of cylindrical shell: maximizing buckling loads while minimizing its weight. In the thermal environment, Golchi et al. [5] studied the thermal buckling and free vibration of functionally graded truncated conical shell stiffened by rings and stringers. Recently, despite not considering stringer, Allahkarami et al. [6] studied the dynamic buckling of a sophisticated bi-directional FG porous cylindrical shell under different boundary conditions and proposed the dynamic instability region of the structure. For the deep doubly curved shell, Naghsh et al. [7] carried out a free vibration analysis of a typical shell of revolution. When the material of the shell is steel, Do et al. [8] performed the impact response of large-diameter thin-walled steel truss stiffened cylinders under the low-speed mass impact. Besides, they also considered the damage to the stringer-stiffened cylinders under external hydrostatic pressure [9]. For the general stringer shell, Bayat et al. provided an approximate analytical expression of the nonlinear free vibration of the truss shell through the extended version of the Hamiltonian method [10] and the homotopy perturbation method [11], respectively. According to different parameters, Lai et al. [12] constructed a low-order analytical approximate solution that is in good agreement with the exact solution based on the harmonic balance method.

Note that few researchers have studied the stability of the stringer shell’s vibration near its equilibrium state and its mathematical expressions, especially when the nonlinear governing equation is linearized and its eigenvalues have a zero real part, which makes the stability of the equilibrium state may be inconsistent between the nonlinear governing system and its linearized system. In this paper, for a structurally orthotropic stringer shell, we mainly analyze the stability of the equilibrium state at the coordinate center of the system and its approximate analytical periodic solution, which is verified by numerical simulation.

The organization of this paper is as follows:

In Section 2, we give the governing dynamic equations of the stringer shell. In Section 3, we analyze the equilibrium states of the system and present an approximate periodic solution around one of the specific types of equilibrium states. In Section 4, we verify the findings in Section 3 through numerical simulations and summarize the obtained results in Section 5.

2. Mathematical Equations of Stringer Shell

We take into account a closed circular cylindrical shell supported by one-dimensional elastic support ribs in two main directions, assuming that the height of the support ribs is petite compared with the radius of curvature and that these non-interacting support ribs are evenly placed at a constant distance (see Figure 1). In this way, the displacement and vibration frequency can be defined accurately.

By using the semi-inextensional theory, the governing equations of an orthotropic stringer shell in terms of large displacement (up to its thickness order) can be written as (see [10] [13] [14] [15])

$\begin{array}{l}{L}_1\left(w\right)={\nabla }_1^{4}w-R\frac{{\partial }^2\varphi }{\partial x^2}+\rho R^2\frac{{\partial }^{2}w}{\partial t^2}-L\left(w,\varphi \right)=0,\\ \frac{1}{B_1}\frac{{\partial }^4\varphi }{\partial y^4}+\frac{1}{R}\frac{{\partial }^{4}w}{\partial x^2}=\frac{1}{2R^2}L\left(w,\varphi \right),\end{array}$ (1)

where

$\begin{array}{l}{\nabla }_1^4=\frac{1}{R^2}\left(D_1\frac{{\partial }^4}{\partial x^4}+2D_3\frac{{\partial }^4}{\partial x^2\partial y^2}+D_2\frac{{\partial }^4}{\partial y^4}\right),\\ L\left(w,\varphi \right)=\frac{{\partial }^{2}w}{\partial x^2}\frac{{\partial }^2\varphi }{\partial y^2}-2\frac{{\partial }^{2}w}{\partial x\partial y}\frac{{\partial }^2\varphi }{\partial x\partial y}+\frac{{\partial }^2\varphi }{\partial x^2}\frac{{\partial }^{2}w}{\partial y^2},\\ \rho ={\rho }_{0}h+\frac{N{\rho }_{1}F}{2\pi R},\\ B_1=\frac{N{E}_{1}F}{2\pi R}+\frac{Eh}{1-{\nu }^2},\end{array}$ (2)

the parameter w represents the normal displacement, R denotes the radius of shell, $\varphi$ is Airy function, ${\rho }_0$ and ${\rho }_1$ are the densities of shell and rib respectively, h is the thickness of shell, N is the number of stringers, F is the transverse section area, $E_1$ and E are young modulus’s of rib and shell respectively, $\nu$ is Poisson ratio, $D_i\left(i=1,2,3\right)$ are the expressions related to the material of stringer shell, mainly including the elasticity modulus, Poisson ratio, size and number of stringer, inertia moment (rotation, torsion) and static moment of stringer’s cross-section, etc., for more details see Chapter 3 of [16].

For simply supported shell that depends on amplitude-frequency, we have

$w=\frac{{\partial }^{2}w}{\partial x^2}=0,x=0,L,$ (3)

the normal displacement w can be approximated as follows

$w\left(x,y,t\right)=f_1\left(t\right)\sin \left(mx\right)\cos \left(ny\right)+f_2\left(t\right){\sin }^2\left(mx\right),$ (4)

where $m=\pi m_1/L$, $m_1$ and n are the wave numbers in the axial and circumferential directions, respectively (see [17]). The relationship between the time-dependent functions $f_1$ and $f_2$ can be obtained by the displacement in the circumferential direction, i.e. $f_2=n^2{f}_1^2/\left(4R\right)$, and then the Air function

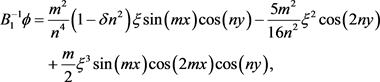(5)

where $\delta =EF/\left(B_{1}LR\right)$ and $\xi =f_1/R$.

By using Galerkin procedure, we obtain the dynamical equation of stringer shell as follows

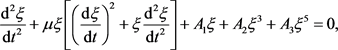(6)

where $\mu =3\rho R^2{n}^4/\left(32B_1\right)$, $A_1={\epsilon }_1+2{\epsilon }_1{\epsilon }_3{n}^2/m^2+{\epsilon }_1{\epsilon }_2{n}^4/m^4+{\left(1-{\delta }^2{n}^2\right)}^2/n^4$, $A_2=1/16+n^4{\epsilon }_1/2-3\left(1-{\delta }^2{n}^2\right)/4$, $A_3=n^4/4$, ${\epsilon }_1=D_1/\left(B_2{R}^2\right)$, ${\epsilon }_2=D_1/D_2$, ${\epsilon }_3=D_3/D_1$, for more details see [16]. Moreover, in terms of the periodic solutions will be investigated in this paper, so the initial conditions $\xi \left(0\right)=c$, $\stackrel{\dot{}}{\xi }\left(0\right)=0$ can be applied.

Note that system (6) can be simply integrated into $T+V=E_e$, where, $V=A_1{\xi }^2/2+A_1{\xi }^4/4+A_3{\xi }^6/6$, and $E_e$ are the kinetic energy, potential energy, as well as the total energy of the system, respectively. The kinetic energy contains more than just the square of velocity, so this system is a non-natural system with fifth-order nonlinear terms [12]. The equilibrium states of the system under various parameters have been discussed preliminary in [12] from a mathematical perspective, but considering the physical properties of the material of the stringer shell in real engineering, parameters $\mu$, $A_1$, $A_3$ can only be greater than zero, and the sign of $A_2$ is arbitrary in this paper. For the convenience of constructing periodic solutions in the next section, we shall take $A_1=1$ in system (6). 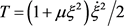In fact, the coefficient $A_1$ of the linear term $\xi$ can also be converted into one by multiplying both sides of the equation by $1/A_1$, and the resulting constant term before the acceleration term can be normalized by time scale transformation.

3. Stability and Approximate Analytical Periodic Solution

Considering system (6) is equivalent to the following form

$\ddot{\xi }+\mu \xi {\stackrel{\dot{}}{\xi }}^2+\mu {\xi }^2\ddot{\xi }+A_1\xi +A_2{\xi }^3+A_3{\xi }^5=0.$ (7)

Let $\stackrel{\dot{}}{\xi }=\eta$, then we obtain

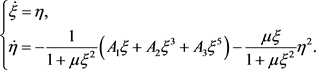(8)

When $\eta =0$, we have $\xi \left(A_1+A_2{\xi }^2+A_3{\xi }^4\right)=0$, i.e. ${\xi }^2=\left(-A_2\pm \sqrt{A_2^2-4A_1{A}_3}\right)/\left(2A_3\right)$ or $\xi =0$. Therefore, system (8) has a unique equilibrium state $\left(0,0\right)$ when $A_2\ge 0$, and for the case of $A_2<0$, system (8) has at most five equilibrium states as follows

$\left(0,0\right)$,

$\left(\sqrt{\frac{-A_2+\sqrt{A_2^2-4A_1{A}_3}}{2A_3}},0\right),\left(-\sqrt{\frac{-A_2+\sqrt{A_2^2-4A_1{A}_3}}{2A_3}},0\right)$,

$\left(\sqrt{\frac{-A_2-\sqrt{A_2^2-4A_1{A}_3}}{2A_3}},0\right),\left(-\sqrt{\frac{-A_2-\sqrt{A_2^2-4A_1{A}_3}}{2A_3}},0\right)$.

More precisely, there are five when $A_2^2-4A_1{A}_3>0$, three when $A_2^2-4A_1{A}_3=0$, and only one when $A_2^2-4A_1{A}_3<0$. Here we temporarily retain the coefficient $A_1$ of the linear term $\xi$ instead of replacing it with the Arabic numeral 1. In this way, without losing generality, we can find in which equilibrium state $A_1$ will play a role.

Note that system (8) is equivalent to

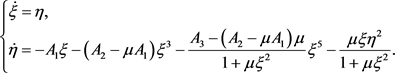(9)

Although it is easy to determine the equilibrium state $\left(0,0\right)$ as a center of the hyperbolic equilibrium states of the linearized equations of system (9) according to the qualitative theory of ordinary differential equation, so the equilibrium state $\left(0,0\right)$ may be the center, focus or center-focus of system (9). For this reason, we will study the type and stability of the equilibrium state $\left(0,0\right)$. If it is also the center of the stringer shell system (9), we will give the approximate analytical expression of the periodic vibration of stringer shell around equilibrium state $\left(0,0\right)$ by using the methods of successor function (see [18] [19] for more details). For some other remaining common equilibrium states, we can move them to the origin of the system by coordinate translation and then study them in the same way.

To this end, let polar coordinate transformation $\xi =a\cos \theta$, $\eta =a\sin \theta$, then system (9) becomes

$\{\begin{array}{c}\begin{array}{c}\frac{\text{d}a}{\text{d}t}=\frac{1}{a}\left(\xi \stackrel{\dot{}}{\xi }+\eta \stackrel{\dot{}}{\eta }\right)\\ =\frac{1}{a}\left[\begin{array}{c}\xi \eta -\frac{\xi \eta }{1+\mu {\xi }^2}\left(A_1+A_2{\xi }^2+A_3{\xi }^4\right)-\frac{\mu \xi {\eta }^3}{1+\mu {\xi }^2}\end{array}\right]\\ =a\cos \theta \sin \theta -\frac{a\cos \theta \sin \theta }{1+\mu a^2{\cos }^2\theta }\left(A_1+a^2{A}_2{\cos }^2\theta +a^4{A}_3{\cos }^4\theta \right)\\ -\frac{\mu a^3\cos \theta {\sin }^3\theta }{1+\mu a^2{\cos }^2\theta }\\ \frac{\text{d}\theta }{\text{d}t}=\frac{1}{{\xi }^2+{\eta }^2}\left(\xi \stackrel{\dot{}}{\eta }-\eta \stackrel{\dot{}}{\xi }\right)\\ =\frac{1}{a^2}\left[\begin{array}{c}-\frac{{\xi }^2}{1+\mu {\xi }^2}\left((A_1+A_2{\xi }^2+A_3{\xi }^4\right)-\frac{\mu {\xi }^2{\eta }^2}{1+\mu {\xi }^2}-{\eta }^2\end{array}\right]\\ =-\frac{{\cos }^2\theta }{1+\mu a^2{\cos }^2\theta }\left(A_1+a^2{A}_2{\cos }^2\theta +a^4{A}_3{\cos }^4\theta \right)\\ -\frac{\mu a^2{\cos }^2\theta {\sin }^2\theta }{1+\mu a^2{\cos }^2\theta }-{\sin }^2\theta \end{array}\end{array}$ (10)

Divide the first equation in system (10) by the second one, yields

$\begin{array}{c}\frac{\text{d}a}{\text{d}\theta }=[a\cos \theta \sin \theta \left(A_1+a^2{A}_2{\cos }^2\theta +a^4{A}_3{\cos }^4\theta \right)+\mu a^3\cos \theta {\sin }^3\theta \\ -a\cos \theta \sin \theta \left(1+\mu a^2{\cos }^2\theta \right)]/[{\cos }^2\theta \left(A_1+a^2{A}_2{\cos }^2\theta +a^4{A}_3{\cos }^4\theta \right)\\ +\mu a^2{\cos }^2\theta {\sin }^2\theta +{\sin }^2\theta \left(1+\mu a^2{\cos }^2\theta \right)]\\ =\frac{\cos \theta \sin \theta \left(A_1-1\right)}{{\cos }^2\theta \left(A_1-1\right)+1}\cdot a\\ +[\sin \theta \cos \theta \left({\cos }^2\theta \left(A_1-1\right)+1\right)\left({\cos }^2\theta \left(A_2-\mu \right)+\mu {\sin }^2\theta \right)\end{array}$

$\begin{array}{l}-{\cos }^3\theta \sin \theta \left(A_1-1\right)\left(A_2{\cos }^2\theta +2\mu {\sin }^2\theta \right)]\cdot a^3\\ +\frac{{\cos }^3\theta \sin \theta }{{\left[{\cos }^2\theta \left(A_1-1\right)+1\right]}^3}[A_3{\cos }^2\theta \left({\cos }^2\theta \left(A_1-1\right)+1\right)\\ +\left({\cos }^2\theta \left(A_1\mu -A_2+\mu \right)-\mu \right)\left({\cos }^2\theta \left(A_2-2\mu \right)+2\mu \right)]\cdot a^5+\mathcal{O}\left(a^7\right)\\ ={\Delta }_{1}a+{\Delta }_2{a}^3+{\Delta }_3{a}^5+\mathcal{O}\left(a^7\right),\end{array}$ (11)

where

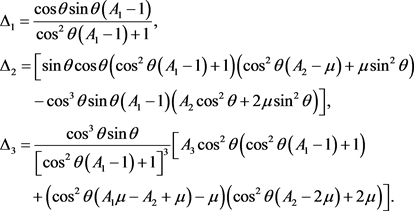
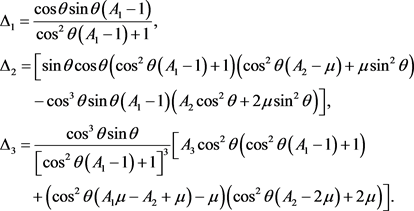
Note that $A_1=1$, i.e.

$\begin{array}{c}\frac{\text{d}a}{\text{d}\theta }=\sin \theta \cos \theta \left({\cos }^2\theta \left(A_2-\mu \right)+\mu {\sin }^2\theta \right)\cdot a^3\\ +{\cos }^3\theta \sin \theta [A_3{\cos }^2\theta +\left({\cos }^2\theta \left(2\mu -A_2\right)-\mu \right)\\ \cdot \left({\cos }^2\theta \left(A_2-2\mu \right)+2\mu \right)]\cdot a^5+\mathcal{O}\left(a^7\right)\\ ={\Delta }_2{a}^3+{\Delta }_3{a}^5+\mathcal{O}\left(a^7\right),\end{array}$ (12)

where

$\begin{array}{l}{\Delta }_2=\sin \theta \cos \theta \left({\cos }^2\theta \left(A_2-\mu \right)+\mu {\sin }^2\theta \right),\\ {\Delta }_3={\cos }^3\theta \sin \theta [A_3{\cos }^2\theta +\left({\cos }^2\theta \left(2\mu -A_2\right)-\mu \right)\\ \cdot \left({\cos }^2\theta \left(A_2-2\mu \right)+2\mu \right)].\end{array}$

In view of the continuous dependence of the solution on the initial value, for the initial condition c, the solution $a\left(\theta ,c\right)$ of system (12) satisfying the initial condition is assumed to admit the following form of convergent power series (see [18])

$a\left(\theta ,c\right)={\displaystyle \underset{k=1}{\overset{+\infty }{\sum }}{a}_k}\left(\theta \right)\cdot c^k.$ (13)

Therefore, we have

$\frac{\text{d}a}{\text{d}\theta }=\frac{\text{d}{a}_1}{\text{d}\theta }\cdot c+\frac{\text{d}{a}_2}{\text{d}\theta }\cdot c^2+\frac{\text{d}{a}_3}{\text{d}\theta }\cdot c^3+\frac{\text{d}{a}_4}{\text{d}\theta }\cdot c^4+\frac{\text{d}{a}_5}{\text{d}\theta }\cdot c^5+\cdots .$ (14)

Substituting systems (13) and (14) into system (12), we obtain that

$\begin{array}{l}\frac{\text{d}{a}_1}{\text{d}\theta }\cdot c+\frac{\text{d}{a}_2}{\text{d}\theta }\cdot c^2+\frac{\text{d}{a}_3}{\text{d}\theta }\cdot c^3+\frac{\text{d}{a}_4}{\text{d}\theta }\cdot c^4+\frac{\text{d}{a}_5}{\text{d}\theta }\cdot c^5+\frac{\text{d}{a}_6}{\text{d}\theta }\cdot c^6+\cdots \\ ={\Delta }_2\cdot c^3+3{\Delta }_2{a}_2\cdot c^4+\left[3{\Delta }_2\left(a_2^2+a_3\right)+{\Delta }_3\right]\cdot c^5\\ +\left[{\Delta }_2\left(a_2^3+6a_2{a}_3+3a_4\right)+5{\Delta }_3{a}_2\right]\cdot c^6\\ +\left[{\Delta }_2\left(3a_2^2{a}_3+6a_2{a}_4+3a_3^2+3a_5\right)+5{\Delta }_3\left(2a_2^2+a_3\right)\right]\cdot c^7+\cdots .\end{array}$ (15)

Based on the initial condition $a\left(0,c\right)=c$, we have $a_1\left(0\right)=1$, $a_l\left(0\right)=0$, $l=2,3,\cdots$. Comparing the coefficients c on both sides of system (15), we have

$\frac{\text{d}{a}_1}{\text{d}\theta }=0,i.e\text{.}{a}_1\left(\theta \right)=1,$ (16)

$\frac{\text{d}{a}_2}{\text{d}\theta }=0,$ (17)

$\frac{\text{d}{a}_3}{\text{d}\theta }={\Delta }_2,$ (18)

$\frac{\text{d}{a}_4}{\text{d}\theta }=3{\Delta }_2{a}_2,$ (19)

$\frac{\text{d}{a}_5}{\text{d}\theta }=3{\Delta }_2\left(a_2^2+a_3\right)+{\Delta }_3.$ (20)

From Equation (17) and $a_2\left(0\right)=0$, we have $a_2\left(\theta \right)=0$, then it can be followed from Equation (18) and $a_3\left(0\right)=0$ that

$\begin{array}{c}{a}_3\left(\theta \right)=a_3\left(0\right)+{\displaystyle {\int }_0^{\theta }\sin }\theta \cos \theta \left[\left(A_2-2\mu \right){\cos }^2\theta +\mu \right]\text{d}\theta \\ =-{\displaystyle {\int }_0^{\theta }\left[\left(A_2-2\mu \right){\cos }^3\theta +\mu \cos \theta \right]\text{d}\cos \theta }\\ =\frac{A_2-2\mu }{4}{\cos }^4\theta +\frac{\mu }{2}{\cos }^2\theta +\frac{A_2}{4}.\end{array}$ (21)

It is easy to find that $a_3\left(\theta \right)$ is a periodic function.

Similarly, we also have $a_4\left(\theta \right)=0$ in terms of Equation (19), $a_2\left(\theta \right)=0$ and $a_4\left(0\right)=0$. Then according to Equation (20) and $a_5\left(0\right)=0$, we obtain

$\begin{array}{c}{a}_5\left(\theta \right)=a_5\left(0\right)+{\displaystyle {\int }_0^{\theta }\left(3{\Delta }_2{a}_3+{\Delta }_3\right)\text{d}\theta }\\ =\frac{5}{32}{A}_2^2+\frac{1}{6}{A}_3+\frac{{\left(A_2-2\mu \right)}^2}{32}{\cos }^8\theta +\frac{3A_2\mu -6{\mu }^2-4A_3}{24}{\cos }^6\theta \\ +\frac{2{\mu }^2+6A_2\mu -3A_2^2}{16}{\cos }^4\theta -\frac{3A_2\mu }{8}{\cos }^2\theta .\end{array}$ (22)

Clearly, $a_5\left(\theta \right)$ is also a periodic function. Continuing with this method, we find that for any $k=1,2,3,\cdots$, $a_{2k}=0$, and $a_{2k+1}$ is a periodic function. That is to say, the trajectories of system (8) near $\left(0,0\right)$ are all periodic orbits, thus $\left(0,0\right)$ is also the center of system (8) and it is a stable equilibrium state. Therefore, the approximate periodic solutions of system (6) around the origin can be determined by $\xi =a\left(\theta \right)\cos \theta$ and its initial values.

4. Numerical Verification

In the previous section, we have proposed an approximate expression of periodic solution of system (8) near the center $\left(0,0\right)$, and some other equilibrium states can be investigated by using the same method. In this section, we use numerical simulation to verify whether there is a periodic solution near the equilibrium state $\left(0,0\right)$ under different parameters (see Figures 2-5).

It can be followed from Figure 2 that system (8) always has a periodic orbit around $\left(0,0\right)$ when $A_2$ is non-negative. In addition, as shown in Figures 3-5, we find that when $A_2^2-4A_1{A}_3>0$, $A_2^2-4A_1{A}_3=0$, and $A_2^2-4A_1{A}_3<0$, the system (8) does have five, three, and unique equilibrium states, respectively, and there are periodic orbits near $\left(0,0\right)$ in all these cases.

5. Conclusion

In this paper, we consider the equilibrium states of a class of structurally orthotropic stringer shell, and refer to the parameter range in its real engineering, its dynamic behavior near the origin is discussed in detail, which is periodic

motion. For several other equilibrium states, we can move them to the origin of the system by coordinate translation respectively, and then study them in the same way. In addition, the conclusion that $\left(0,0\right)$ is the center of the nonlinear system can also be obtained according to the principle of symmetry [20]. However, according to the successor function method, we not only give the approximate expression of this periodic motion but also verify the rationality of the results by numerically simulating its four kinds of phase portraits. It is hoped that the obtained results will be helpful to study the dynamic behavior of other shell structures.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (NSFC) through grant No.11672259 and the China Scholarship Council through grant No.201908320086.

Conflicts of Interest

The authors declare that there is no competing interest.

References

[1]	Palazotto, A.N. (1977) Bifurcation and Collapse Analysis of Stringer and Ring-Stringer Stiffened Cylindrical Shells with Cutouts. Computers &Structures, 7, 47-58. https://doi.org/10.1016/0045-7949(77)90059-1
[2]	Gavrilenko, G.D. and Matsner, V.I. (2006) Some Features of the Buckling of Stringer Shells. International Applied Mechanics, 42, 176-180. https://xs.scihub.ltd/ https://doi.org/10.1007/s10778-006-0073-4
[3]	Schilling, J.C. and Mittelstedt C. (2020) Local Buckling Analysis of Omega-Stringer-Stiffened Composite Panels Using a New Closed-Form Analytical Approximate Solution. Thin-Walled Structures, 147, Article ID: 106534. https://doi.org/10.1016/j.tws.2019.106534
[4]	Khodaygan, S. and Bohlooly, M. (2020) Multi-Objective Optimal Design of Stiffened Laminated Composite Cylindrical Shell with Piezoelectric Actuators. International Journal on Interactive Design and Manufacturing. https://xs.scihub.ltd/ https://doi.org/10.1007/s12008-020-00644-1
[5]	Golchi, M., Talebitooti, M. and Talebitooti, R. (2019) Thermal Buckling and Free Vibration of FG Truncated Conical Shells with Stringer and Ring Stiffeners Using Differential Quadrature Method. Mechanics Based Design of Structures and Machines, 47, 255-282. https://doi.org/10.1080/15397734.2018.1545588
[6]	Allahkarami, F., Tohidi, H., Dimitri, R. and Tornabene, F. (2020) Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Applied Sciences, 10, 1345. https://doi.org/10.3390/app10041345
[7]	Naghsh, A., Saadatpour, M.M. and Azhari, M. (2015) Free Vibration Analysis of Stringer Stiffened General Shells of Revolution Using a Meridional Finite Strip Method. Thin-Walled Structures, 94, 651-662. https://doi.org/10.1016/j.tws.2015.05.015
[8]	Do, Q.T., Muttaqie, M., Shin, H.K. and Cho, S.R. (2018) Dynamic Lateral Mass Impact on Steel Stringer-Stiffened Cylinders. International Journal of Impact Engineering, 116, 105-126. https://doi.org/10.1016/j.ijimpeng.2018.02.007
[9]	Do, Q.T., Muttaqie, M., Park, S.H., Shin, H.K. and Cho, S.R. (2018) Ultimate Strength of Intact and Dented Steel Stringer-Stiffened Cylinders under Hydrostatic Pressure. Thin-Walled Structures, 132, 442-460. https://doi.org/10.1016/j.tws.2018.09.010
[10]	Bayat, M., Pakar, I. and Cveticanin, L. (2014) Nonlinear Vibration of Stringer Shell by Means of Extended Hamiltonian Approach. Archive of Applied Mechanics, 84, 43-50. https://xs.scihub.ltd/ https://doi.org/10.1007/s00419-013-0781-2
[11]	Pakar, I. and Bayat, M. (2015) Nonlinear Vibration of Stringer Shell: An Analytical Approach. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 229, 44-51. https://doi.org/10.1177/0954408913509090
[12]	Lai, S.K., Yang X. and Gao F.B. (2019) Analytical Analysis of Large-Amplitude Oscillation in Triple-Well Non-Natural Systems. Journal of Computational and Nonlinear Dynamics, 14, Article ID: 091002. https://doi.org/10.1115/1.4043833
[13]	Bayat, M., Pakar, I. and Bayat, M. (2013) Analytical Solution for Nonlinear Vibration of an Eccentrically Reinforced Cylindrical Shell. Steel and Composite Structures, 14, 511-521. https://doi.org/10.12989/scs.2013.14.5.511
[14]	Evakin, A. and Kalamkarov, A. (2001) Analysis of Large Deflection Equilibrium State of Composite Shells of Revolution: Part 1. General Model and Singular Perturbation Analysis. International Journal of Solids and Structures, 38, 8961-8974. https://doi.org/10.1016/S0020-7683(01)00184-6
[15]	Andrianov, I.V., Awrejcewicz, J. and Manevitch, L.I. (2004) Asymptotical Mechanics of Thin-Walled Structures. Springer-Verlag, Berlin, Heidelberg. https://doi.org/10.1007/978-3-540-45246-1
[16]	Awrejcewicz, J., Andrianov, I.V. and Manevitch, L.I. (1998) Asymptotic Approaches in Nonlinear Dynamics: New Trends and Applications. Springer-Verlag, Berlin, Heidelberg. https://doi.org/10.1007/978-3-642-72079-6
[17]	Dowell, E.H. and Ventres, C.S. (1968) Modal Equations for the Nonlinear Flexural Vibrations of a Cylindrical Shell. International Journal of Solids and Structures, 4, 975-991. https://doi.org/10.1016/0020-7683(68)90017-6
[18]	Liu, Y.R., Li, J.B. and Huang, W.T. (2014) Planar Dynamical Systems: Selected Classical Problems. Walter de Gruyter GmbH & Co KG, Germany. https://doi.org/10.1515/9783110298369
[19]	Zhang, Z.F., Ding, T.R., Huang, W.Z. and Dong, Z.X. (2006) Qualitative Theory of Differential Equations. American Mathematical Society, Washington DC.
[20]	Lu, Q.S. (1989) Qualitative Method and Bifurcation of Ordinary Differential Equations. Beihang University Press, Beijing. (In Chinese)