The Interaction and Degeneracy of Mixed Solutions for Derivative Nonlinear Schrödinger Equation ()
1. Introduction
The Derivative Nonlinear Schrödinger(DNLS) equation
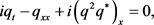(1)
plays an important role in plasma physics and nonlinear optics. Firstly, the DNLS equation is used to describe the evolution of small but finite amplitude Alfvén waves that propagate quasi-parallel to the magnetic field [1] [2] and large-amplitude magnetohydrodynamic waves in plasmas [3] [4]. Secondly, the DNLS equation governs the propagation of sub-picosecond or femtosecond pulses in single-mode optical fibers [5] [6] [7]. Here “*” denotes the complex conjugation, and subscript of x (or t) denotes the partial derivative with respect to x (or t).
For the DNLS equation with vanishing boundary condition, Kaup and Newell [8] firstly obtained the one-soliton solutions of the DNLS equation by the inverse scattering transform, and showed that this solution becomes the algebraic soliton in a certain limiting condition. Determinant expression of the N-soliton solution [9] for the DNLS equation can be expressed by Darboux transformation. Under non-vanishing boundary conditions, Kawata and Inoue [10] developed an inverse scattering transform of the DNLS equation and introduced the so-called “paired soliton”, which is now regarded as the breather solution. With the help of introducing an affine parameter, Chen and Lam [11] revised the inverse scattering transform and then got the single breather solution, which can become the dark soliton and the bright soliton. The rogue waves [12] [13] [14] [15] can be derived from the degeneration of breather solutions by the Darboux transformation [16] [17], which is a very powerful method in integrable nonlinear systems [18] [19] [20] [21].
Rogue waves have recently been studied in a plethora of physical settings, such as deep ocean waves [26], optical fibers [22] [23], and water tanks [24] [25]. The physical mechanisms of rogue wave’s generation in many physical systems have been the subject of many research studies [27] [28] [29] [30] [31]. Rogue wave, “appear from nowhere and disappear without a trace” [33], is credited with the Peregrine soliton [32] of the nonlinear Schrödinger (NLS) equation. The Peregrine soliton, which possesses a high amplitude and two hollows, is usually expressed in terms of a simple rational algebraic formula. By the limitation of the infinitely large period of the Kuznetsov-Ma breather [34] [35] and the Akhmediev breather [36] of the NLS equation, the rogue waves can be generated.
The large amplitude waves can be generated from the instability of small amplitude perturbations that are usually chaotic and may contain many frequencies in their spectra. This fact strongly suggests that rogue waves are generally described by adjusting the relative phases of the multiphase solutions and breather solutions of the corresponding nonlinear evolution equations [37] [38] [39].
The aim of this paper is to study the mixed solutions of the DNLS equation and their degeneration mechanism, which implies the obtaining of rogue waves by the synchronization of the mixed solutions: phase solutions and breather solutions. Further, a superposition of mixed solutions may create a hybrid solution, such as a breather solution with periodic conditions, by means of different choices of the phases in the corresponding analytical formulas.
The structure of this paper is as follows. In Section 2, we provide analytically the determinant representation of the mixed solutions. In Section 3, the mixed solutions and their key properties such as the interaction and the degeneration mechanism are discussed. In the limitation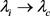
, rogue waves, and breather solution with periodic conditions, are generated from the degeneration technique of the mixed solutions: the phase solutions and breather solutions. Finally, we summarize our main results in Section 4.
2. Mixed Solutions
The DNLS equation [8] can be given by the integrability condition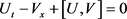 
of the following Kaup-Newell spectral system (Lax pair) with the reduction condition
. The Lax pairs can be constructed as follows:
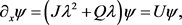(2)
(3)
with
(4)
(5)
here
, an arbitrary complex number, is called the eigenvalue (or the spectral parameter), and 
is called the eigenfunction associated with the eigenvalue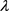 
of the Kaup-Newell system.
The general forms of the the mixed solutions [15] are given by using the Darboux transformation and determinant representation of the DNLS equation,
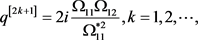(6)
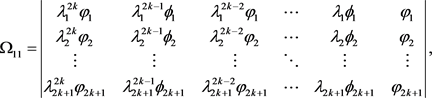
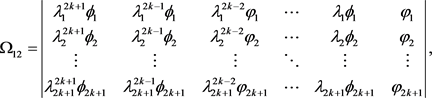
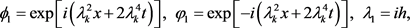
Notice that the denominators 
are moduli of two non-zero complex functions from Darboux transformation, so the new solution ![]()
is non-singular.
3. The Interaction and Degeneracy of Mixed Solutions
The interaction and degeneration of mixed solutions of the DNLS equation can be illustrate by the Equation (6). We mainly consider the function of the parameters ![]()
and h on the generation of the large amplitude waves and rogue waves. For convenience without losing generality, we only consider![]()
. The
density plot of the 2-phase solution ![]()
with the fixed parameters ![]()
and ![]()
and the variable parameter ![]()
(![]()
, ![]()
, and![]()
) is
shown in Figure 1. Since the variable parameter ![]()
is a purely imaginary, the phase solutions are given by Equation (6). It can give that the rogue waves can constructed by adjusting the the variable parameter![]()
, i.e.![]()
. Given that the variable parameter ![]()
is a real number, the density plot of the 1-breather
solution ![]()
with the fixed parameters ![]()
and ![]()
and the variable parameter ![]()
(![]()
, ![]()
, and![]()
) is shown in Figure 2. Note that the
degeneration procedure of the 2-phase solutions and 1-breather solution is constructed by performing the limitation ![]()
and![]()
, i.e. ![]()
. In this limitation, we obtain the same rational solution
![]()
![]()
(7)
By letting![]()
, so![]()
, the maximum amplitude of ![]()
occurs at (![]()
) and is equal to![]()
, and the minimum amplitude of ![]()
occurs at (![]()
) and is equal to 0. Obviously, this rational solution is a rogue wave; see the panel (c) in Figure 1 and Figure 2.
In order to have a better understanding of the degeneration procedure of the mixed solutions, a hybrid solution,
![]()
![]()
![]()
(8)
is considered as a phase-breather solution shown in Figure 3.
The solution is constructed by letting![]()
, i.e.![]()
, where![]()
, ![]()
, ![]()
and![]()
. Thus by adjusting the relative phases of the
mixed solutions in the interacting area, namely, taking the limitation![]()
, i.e.![]()
, it can obtain the same rogue wave solution (see in Equation (7)).
4. Summary
In this paper, we have shown that rogue waves and some hybrid solutions can be obtained by the synchronization of the mixed solutions: phase solutions and breather solutions. The rogue wave is generated by adjusting the parameters ![]()
and h, the limitation![]()
, where![]()
, ![]()
being an arbitrary real number. The results provide new insights into the generation of the large amplitude waves and rogue waves, and thus are useful in the application or prevention of the large amplitude waves and rogue waves in the propagation of sub-picosecond or femtosecond pulses. Next we will consider the application of these results to physical theory and experiments and its relation with the initial boundary value problem is also considered.
Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grant No. 11601187 and Major SRT Project of Jiaxing University.