Yijian Ge
School of Science, University of Shanghai for Science and Technology, Shanghai, China.
DOI: 10.4236/apm.2019.910043   PDF    HTML   XML   755 Downloads   1,442 Views   Citations

Abstract

In this paper, we study the existence of solution for some p(x)-polyharmonic Kirchhoff equations. The latter is allowed to vanish at the origin (degenerate case). Firstly, we study the existence of solutions of approximate equations. Secondly, we prove the existence of the solutions of the original equation. The main tool is the Schauder’s Theorem.

Keywords

p(x)-polyharmonic Kirchhoff Equations, Existence of Solutions, Schauder’s Fixed Point Theorem

Share and Cite:

1. Introduction

In this paper, we prove the existence of solution of Dirchlet problems involving the p-polyharmonic operators ${\Delta }_p^s$. We consider

$\{\begin{array}{l}M\left({\Vert u\Vert }^p\right){\Delta }_p^{s}u+a\left(x\right)g\left(u\right)=f\left(x\right)\text{in}\Omega \mathrm{,}\\ {D^{\alpha }u\left(x\right)|}_{\partial \Omega }=0\forall \alpha \mathrm{,}\text{with}\left|\alpha \right|\le s-\mathrm{1,}\end{array}$ (1)

where $\Omega \subset {ℝ}^N$ is a bounded domain, $p\ge 2$, $s=1,2,\cdots$, $\Vert \cdot \Vert$ is denoted in section 2, and $f\left(x\right)\in L^1\left(\Omega \right)$, $0\le a\left(x\right)\in L^1\left(\Omega \right)$. Here, the p-polyharmonic operator is defined by

${\Delta }_p^{s}u=\{\begin{array}{l}-div{\Delta }^{j-1}\left({\left|D{\Delta }^{j-1}u\right|}^{p-2}\right)D{\Delta }^{j-1}u,s=2j-\mathrm{1,}\\ {\Delta }^j\left({\left|{\Delta }^{j}u\right|}^{p-2}{\Delta }^{j}u\right),s=2j\mathrm{,}\end{array}j=\mathrm{1,2,}\cdots$, (2)

which becomes the usual p-Laplacian for $s=1$. Kratochvl and Necâs introduced the p-biharmonic operator in [1] [2] [3] to study the physical equations, the p-biharmonic operator for $s=2$ and the polyharmonic operator for $p=2$, which reduces to the more appoximate case

$\{\begin{array}{l}M\left({\Vert u\Vert }^2\right){\left(-\Delta u\right)}^s=f\left(x\mathrm{,}u\right)\text{in}\Omega \mathrm{,}\\ {D^{\alpha }u\left(x\right)|}_{\partial \Omega }=0\forall \alpha \mathrm{,}\text{with}\left|\alpha \right|\le s-1\end{array}$. (3)

We introduce for $s=1,2,\cdots$, the main s-order differential operator

${\mathcal{D}}_{s}u=\{\begin{array}{l}D{\Delta }^{j-1}u\text{if}s=2j-\mathrm{1,}\\ {\Delta }^{j}u\text{if}s=2j\end{array}j=\mathrm{1,2,}\cdots$. (4)

Note that ${\mathcal{D}}_s$ is an n-vectorial operator when s is odd and $n>1$, while it is a scalar operator when s is even.

In our hypothesis, the Kirchhoff function $M\mathrm{<mo>\; :\; </mo>}{R}_0^{+}\to R_0^{+}$ is assumed to be continuous and to verify the structural assumptions (M):

(M₁) M is non-decreasing;

(M₂) there exists a number $\gamma \in \left[\mathrm{1,}{p}_s\right)$ such that for all $t\in R_0^{+}$ ;

$tM\left(t\right)\le \gamma \hat{M}\left(t\right)\mathrm{,}\text{where}\hat{M}\left(t\right)={\displaystyle {\int }_0^t}M\left(\theta \right)\text{d}\theta \mathrm{<mo>\; ;\; </mo>}$

(M₃) for all $t\ge \sigma$, there exists $m_0=m_0\left(\sigma \right)>0$ such that $M\left(t\right)\ge m_0$ for all $\sigma \ge 0$.

We introduce the Sobolev critical exponent $p_s^{\mathrm{<mo>\; *\; </mo>}}$ and the number $p_s$ defined by following

$p_s^{*}=\{\begin{array}{l}\frac{np}{n-sp}\text{if}n>sp,\hfill \\ \infty \text{if}n\le sp.\hfill \end{array}$ $p_s=\frac{p_s^{*}}{p}=\{\begin{array}{l}\frac{n}{n-sp}\text{if}n>sp,\hfill \\ \infty \text{if}n\le sp.\hfill \end{array}$ (5)

A very special Kirchhoff function verifying (M) is denoted by

$M\left(t\right)=a+b\gamma t^{\gamma -1},a,b\ge 0,a+b>0,\gamma \{\begin{array}{l}\in \left(1,p_s\right)\text{if}b>0,\\ =1\text{if}b=0.\end{array}$ (6)

when M is of the type (6) and $a>0,b\ge 0$, problem (1) is said to be non-degenerate, while it is called degenerate if $a=0$. Besides, problem (2) reduces to the usual well-known quasilinear elliptic equation while $a>0,b=0$. The existence of positive solutions of non-degenerate Kirchhoff-type problems has been proved in [4] [5] for $L=1$. The novelty of this paper is to treat the degenerate case with allowing Kirchhoff function to take the zero value. Several authors have considered fourth order problems with nonlinear boundary conditions involving third order derivatives, see [6]. The classical counterpart of our problem models containning several interesting phenomena were deeply studied in physicals even in the one-dimensional case. It dates back to 1883 when Kirchhoff proposed his celebrated equation:

$\rho \frac{{\partial }^{2}u}{\partial t^2}-\left(\frac{P_0}{h}+\frac{E}{2L}{\displaystyle {\int }_0^L}{\left|\frac{\partial u}{\partial x}\right|}^2\text{d}x\right)\frac{{\partial }^{2}u}{\partial x^2}=0$,

as a nonlinear extension of D’Alambert’s wave equation for free vibrations for elastic strings.

Here we study a stationary version of Kirchhoff-type problems, where $u=u\left(x\right)$ is the lateral displacement at the space coordinate $\chi$ and M is typically a line with positive slope. Our result allows M to have this property. The classical Kirchhoff theory described further details and physical models, which can be found in [7] [8]. In the standard case $L=2$, problem of type (2) arise in the theory of bending extensible elastic beams. There $u=u\left(x\right)$ denotes a thin extensible elastic beam. The function f models a small changes with effect in the length of beam but acts as a force exerted on the beam. We read to [6] and the references therein for a discussion about modelling of Kirchhoff-type strings and beams. We cite the wide literature on the subject, the works [9] [10] [11] [12], where Kirchhoff-type problems new studied by exploiting different methods.

We recall that study of semilinear case with datum $f\left(x\right)\in L^1\left(\Omega \right)$ in [13] [14] [15] [16], with respect to (1), we assume that the coefficient $a\left(x\right)$ of the zero order term and to the datum $f\left(x\right)$, in addition to imposing that

$f\left(x\right)\mathrm{,}a\left(x\right)\in L^1\left(\Omega \right)$, (7)

and there exists $Q>0$ such that, for $x\in \Omega$ a.e.,

$\left|f\left(x\right)\right|\le Qa\left(x\right)\mathrm{.}$ (8)

There is assumption that $g\left(s\right)$ is continuous function satisfies

$\underset{s\to -\infty }{\lim }g\left(s\right)=-\infty \text{and}\underset{s\to +\infty }{\lim }g\left(s\right)=\infty \mathrm{.}$ (9)

There has been an increasing interest in studying equations involving p(x)-Laplace operators over the last few decades. Motivated by theoretical research in the regularizing effect of the interaction between the coefficient of the zero order term and the datum $f\left(x\right)\in L^1\left(\Omega \right)$ in some nonlinear Dirchlet problems, we pay attention to the existence of solutions for p(x)-polyharmonic Kirchhoff equations. Now we consider the problems

$\{\begin{array}{l}M\left(\phi \left(u\right)\right){\Delta }_{p\left(x\right)}^{s}u+a\left(x\right)g\left(u\right)=f\left(x\right)\text{in}\Omega \mathrm{,}\\ {D^{\alpha }u\left(x\right)|}_{\partial \Omega }=0\forall \alpha \mathrm{,}\text{with}\left|\alpha \right|\le s-\mathrm{1,}\end{array}$ (10)

where $\Omega \subset ℝ$ is a bounded domain Lipschitz boundary, M is a degenerate Kirchhoff function and $p\in C\left(\bar{\Omega }\right)$. More details and conditions are given in section 4. The p(x)-polyharmonic operator is given by

${\Delta }_{p\left(x\right)}^{s}u=\{\begin{array}{l}-div{\Delta }^{j-1}\left({\left|D{\Delta }^{j-1}u\right|}^{p\left(x\right)-2}\right)D{\Delta }^{j-1}u,s=2j-\mathrm{1,}\\ {\Delta }^j\left({\left|{\Delta }^{j}u\right|}^{p\left(x\right)-2}{\Delta }^{j}u\right),s=2j\mathrm{,}\end{array}j=\mathrm{1,2,}\cdots$. (11)

The author exploits the symmetric mountain pass theorem to proves the multiplicity of solutions for p(x)-polyharmonic elliptic Kirchhoff equations in [17]. In contrast, in this paper, the keystone of the proofs them is the deduction, by condition (7), (8), of the $L^{\infty }$ -estimate of the approximated solutions, we prove the problem existing a solution $u\in W_0^{s\mathrm{.}p(\cdot )}\left(\Omega \right)\cap L^{\infty }\left(\Omega \right)$.

This paper is organized as follows. In Section 2, we introduce some basic notation and properties in variable exponent Sobolev spaces. In Section 3, we prove the problem (1) ( $p\equiv \text{Const}$ ) existing a solution $u\in W_0^{s\mathrm{.}p}\left(\Omega \right)\cap L^{\infty }\left(\Omega \right)$. In Section 4, we treat the more delicate case $p=p\left(x\right)$.

2. Notations and Preliminaries

In this section, we briefly introduce some basic results and notations. Let $\Omega$ be a bounded domain in ${ℝ}^N$, we denote a multi-index $\alpha =\left({\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}\cdots \mathrm{,}{\alpha }_n\right)\in {\mathbb{N}}_0^n$, with length $\left|\alpha \right|={\displaystyle {\sum }_{i=1}^n}{\alpha }_i\le s$, such that the corresponding partial differentation:

$D^{\alpha }=\frac{{\partial }^{\left|\alpha \right|}}{\partial x_1^{{\alpha }_1}\partial x_2^{{\alpha }_2}\cdots \partial x_n^{{\alpha }_n}}$.

Write:

${\Vert u\Vert }_{W^{s\mathrm{,}p}\left(\Omega \right)}={\left({\displaystyle \underset{\left|\alpha \right|\le s}{\sum }}{\Vert D^{\alpha }u\Vert }^p\right)}^{\frac{1}{p}}\mathrm{,}$ (12)

where ${\Vert \cdot \Vert }_p$ denotes the standard $L^p$ -norm. See [18], we denote the space $W_0^{s\mathrm{,}p}\left(\Omega \right)$ is the completion of $C_0^{\infty }\left(\Omega \right)$ with respect to the standard norm of $W^{s\mathrm{,}p}\left(\Omega \right)$. Moreover, denote ${\mathcal{D}}^{s\mathrm{,}p}\left(\Omega \right)$ be the completion of $C_0^{\infty }\left(\Omega \right)$, with respect to the norm:

${\Vert u\Vert }_{{\mathcal{D}}^{s\mathrm{,}p}\left(\Omega \right)}={\left({\displaystyle \underset{\left|\alpha \right|=s}{\sum }}{\Vert D^{\alpha }u\Vert }^p\right)}^{\frac{1}{p}}$. (13)

By the poncaré inequality, there exists a positive constant $\mathcal{K}=\mathcal{K}\left(n\mathrm{,}p\mathrm{,}\Omega \right)$, with $m=s,p\ge 1$, such that

${\Vert u\Vert }_{W^{s\mathrm{,}p}\left(\Omega \right)}\le \mathcal{K}{\Vert u\Vert }_{D^{s\mathrm{,}p}\left(\Omega \right)}\mathrm{,}\forall u\in W_0^{s\mathrm{,}p}\left(\Omega \right)\mathrm{.}$ (14)

Hence, we obtain that the norms ${\Vert \cdot \Vert }_{W^{s\mathrm{,}p}\left(\Omega \right)}$ are equivalent, so that the two completions of $C_0^{\infty }\left(\Omega \right)$, with corresponding these norms, namely

$W_0^{s\mathrm{,}p}\left(\Omega \right)={\mathcal{D}}^{s\mathrm{,}p}\left(\Omega \right).$

We endow the vectorial space ${\left[L^p\left(\Omega \right)\right]}^n$, with respect to the norm

${\Vert v\Vert }_p={\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}}{\Vert {\beta }_i\Vert }_p^p\right)}^{\frac{1}{p}},$ (15)

where $v=\left({\beta }_1,{\beta }_2,\cdots ,{\beta }_n\right)$ and $n>1$, we still use the same symbol ${\Vert \cdot \Vert }_p$ to denote both the standard $L^p$ -norm in the scalar space $L^p\left(\Omega \right)$ and the norm define in (15), in the vectorial space ${\left[L^p\left(\Omega \right)\right]}^n$.

For $s=2,1<p<\infty$, by the Caldéron-Zygmund inequality, see details in [19] [20], there exists a constant $k_2=k_2\left(n,p\right)>0$ such that:

${\Vert u\Vert }_{{\mathcal{D}}^{\mathrm{2,}p}\left(\Omega \right)}\le k_2{\Vert {\mathcal{D}}_{2}u\Vert }_p,\forall u\in W_0^{\mathrm{2,}p}\left(\Omega \right)\mathrm{.}$ (16)

Proposition 2.1. If $p\in \left(\mathrm{1,}\infty \right)$ and $s=1,2,\cdots$, then there exists a positive constant $k_s=k_s\left(n,p\right)$ such that:

${\Vert u\Vert }_{{\mathcal{D}}^{s\mathrm{,}p}\left(\Omega \right)}\le k_s{\Vert {\mathcal{D}}_{s}u\Vert }_p,\forall u\in W_0^{s\mathrm{,}p}\left(\Omega \right)\mathrm{.}$ (17)

where ${\mathcal{D}}_s$ is denoted in (4), see also in [17].

Hence, from now on we endow $W_0^{s\mathrm{,}p}\left(\Omega \right)$ with the norm $\Vert \cdot \Vert ={\Vert {\mathcal{D}}_s\cdot \Vert }_p$, which is equivalent to the standard Sobolev norm.

Remark 2.1. For all $s=1,2,\cdots$, $1<p<\infty$. $W_0^{s,p}\left(\Omega \right)$ is a separable, uniformly convex, reflexive, real Banach space.

Note that, when $p=2$, this norm is introduced by the inner product

$\langle u\mathrm{,}v\rangle ={\displaystyle {\int }_{\Omega }}{\mathcal{D}}_{s}u{\mathcal{D}}_{s}v\text{d}x\mathrm{,}\forall u\mathrm{,}v\in H_0^s\left(\Omega \right),$ (18)

when s is even the operation between ${\mathcal{D}}_{s}u$ and ${\mathcal{D}}_{s}v$ is scalar multiplication, while s is odd, it is the n-Euclidean scalar product.

Lemma 2.1. See [21] (Schuader’s theorem) Let F be a completely continuous map and let K be a convex, bounded, closed and invariant subset of X. Then F has a fixed point in K.

F is completely continuous map:

1) F is continuous.

2) For every B is bounded subset of X, then $\overline{F\left(B\right)}$ is compact.

Proposition 2.2. See [18], for $1\le h<p_s^{*}$, the embedding $W_0^{s\mathrm{,}p}\left(\Omega \right)\mathrm{,}{L}^h\left(\Omega \right)$ is compact and continuous, there exists ${\delta }_h={\delta }_h\left(n,p,s,\Omega \right)>0$, such that:

${\Vert u\Vert }_h\le {\delta }_h\Vert u\Vert \mathrm{,}\forall u\in W_0^{s\mathrm{,}p}\left(\Omega \right)\mathrm{.}$ (19)

We study problem (1) for a solution, we understand:

$\{\begin{array}{l}u\in W_0^{s\mathrm{,}p}\left(\Omega \right)\cap L^{\infty }\left(\Omega \right)\mathrm{,}\\ M\left({\Vert u\Vert }^p\right){\displaystyle {\int }_{\Omega }}{\left|{\mathcal{D}}_{s}u\right|}^{p-2}{\mathcal{D}}_{s}u{\mathcal{D}}_{s}v\text{d}x+{\displaystyle {\int }_{\Omega }}a\left(x\right)g\left(u\right)\phi ={\displaystyle {\int }_{\Omega }}f\left(x\right)\phi \mathrm{,}\\ \phi \in W_0^{s\mathrm{,}p}\left(\Omega \right)\cap L^{\infty }\left(\Omega \right)\mathrm{.}\end{array}$ (20)

where ${\mathcal{D}}_s$ is the operator in (4) and ${\displaystyle {\int }_{\Omega }}{\left|{\mathcal{D}}_{s}u\right|}^{p-2}{\mathcal{D}}_{s}u{\mathcal{D}}_{s}v\phi \text{d}x$ is the p-polyharmonic operator ${\Delta }_p^s$ in weak sense.

3. Existence and Uniqueness of Solution for (1)

In order to study the solution of problem (1), we consider problems:

$\{\begin{array}{l}M\left({\Vert u_n\Vert }^p\right){\Delta }_p^s{u}_n+a_n\left(x\right)g\left(u_n\right)=f_n\text{in}\Omega \mathrm{,}\\ {D^{\alpha }{u}_n\left(x\right)|}_{\partial \Omega }=0\forall \alpha \mathrm{,}\text{with}\left|\alpha \right|\le s-1.\end{array}$ (21)

where $\Omega$ is a bounded domain in ${ℝ}^N$, $p\in \left[\mathrm{2,}\infty \right)$, and $s=1,2,\cdots$. Indeed, suppose $f\left(x\right)\in L^1\left(\Omega \right)$, $0\le a\left(x\right)\le L^1\left(\Omega \right)$, and exist $h\left(x\right)\in L^{q\text{'}}\left(\Omega \right)$, then $\left|g\left(s\right)\right|\le h\left(x\right)$.

Let us define:

$a_n\left(x\right)=\frac{a\left(x\right)}{1+\frac{Q}{n}\left|a\left(x\right)\right|},f_n\left(x\right)=\frac{f\left(x\right)}{1+\frac{1}{n}\left|f\left(x\right)\right|}.$ (22)

and that we choose $k_0>0$, such that

$g\left(t\right)t\ge \mathrm{0,}\left|g\left(t\right)\right|\ge Q\mathrm{.}$ (23)

for every $t\ge k_0$.

Theorem 3.1. There is a solution $u_n\in W_0^{s\mathrm{,}p}\left(\Omega \right)$ to the problem (21).

Proof. Since $\phi =s{\left(1+\frac{s}{n}\right)}^{-1}$ is increasing, we deduced by (8) that,

$\left|f_n\left(x\right)\right|=\frac{\left|f\left(x\right)\right|}{1+\frac{1}{n}\left|f\left(x\right)\right|}\le \frac{Qa\left(x\right)}{1+\frac{Q}{n}a\left(x\right)}=Q{a}_n\left(x\right).$ (24)

We define:

$J\left(\omega \right)=\frac{1}{p}\hat{M}\left({\Vert \omega \Vert }^p\right)+{\displaystyle {\int }_{\Omega }}{a}_n\left(x\right)g\left(v\right)\omega -{\displaystyle {\int }_{\Omega }}{f}_n\left(x\right)\omega \mathrm{,}$

where $v\in W_0^{s\mathrm{,}p}\left(\Omega \right)$, by M₂ and (24), we can get

$J\left(\omega \right)\ge \frac{b}{p}{\Vert \omega \Vert }^{p\gamma }-{\displaystyle {\int }_{\Omega }}{a}_n\left(x\right)\left|g\left(v\right)-Q\right|\omega \mathrm{,}$

by the Hölder’s inequality and the Poincaré equality, then

$J\left(\omega \right)\ge \frac{b}{p}{\Vert \omega \Vert }^{p\gamma }-C{a}_n\left(x\right){\Vert g\left(v\right)-Q\Vert }_{L^{q^{\prime }}}\Vert \omega \Vert \mathrm{,}$

since $p\ge 2$ and $\gamma \in \left(\mathrm{1,}{p}_s\right)$, then $J\left(\omega \right)$ is bounded, coercive and weakly lower semicontinuous, such that $J\left(\omega \right)$ has a minimizer and the Euler equation is:

$M\left({\Vert \omega \Vert }^p\right){\Delta }_p^s\omega +a_n\left(x\right)g\left(v\right)=f_n\mathrm{.}$

Moreover, such a minimizer is unique, by the strict convexity of J.

Fixed $n\in N$, let $v\in W_0^{s\mathrm{,}p}\left(\Omega \right)$, define $\omega =S\left(v\right)$ to be the unique solution of the problem:

$\{\begin{array}{l}M\left({\Vert \omega \Vert }^p\right){\Delta }_p^s\omega +a_n\left(x\right)g\left(v\right)=f_n\text{in}\Omega \mathrm{,}\\ {D^{\alpha }u\left(x\right)|}_{\partial \Omega }=0.\forall \alpha \mathrm{,}\text{with}\left|\alpha \right|\le s-1.\end{array}$ (25)

We will use the as a test in (25), we get

by (M₁, M₃), (22), (24) and Hölder’s inequality, we obtain

where, and is the conjugate exponent of q, by (23) and the Poincaré equality, it follows that

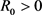We take, so that the ball of radius is invariant

under s in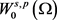. In order to apply the Schauder’s Fixed Point Theorem, apart from the invariant, we need to check the continuity and compactness of s as an operator from 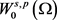to. So, the proof will be divided into two steps.

Step 1: We prove the continuity. In order to do this, we define and then:

(26)

Since the convergence of 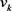in, by (26) we obtain:

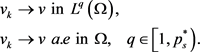(27)

In fact, let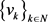, be a sequence in converging to.

To this end, by choosing as a test function, we have

by the inequality, for, and, by Hölder’s inequality, we obtain

(28)

as,

where is bounded, then by (27), and, there is, hence S is continuous from to.

Step 2. We prove S is compact, first we take a sequence that, therefore by Rellich-Kondrachov Theorem, we obtain

(29)

Since S is continuous,.

with S is a positive constant, independent of k, such that,

(30)

Because of the continuity of S, necessarily, so that proceeding as in (28), we can get:

as, the second term of left hand is vanished by (29) and (30). we can conclude

and therefore S is compact.

Hence, by lemma 2.1, there exists a solution of problem (21), next we will prove the problem (1).

We will use the following function defined for, by

(31)

We use as a test function in approximate problem (21), then

by (M₁, M₃), and (24) we obtain:

(32)

by (9) and (23), this means:

(33)

which by (33) implies that and the sequence is bounded in.

Next, we use as a test function to deduce, such that,

by and (23) we can get

(34)

then,

(35)

and we obtain that is bounded in and a sequence, still denoted, which converges weakly in and a.e. to u with.

Moreover, using that, we obtain by the dominated convergence theorem, the convergence of the sequence to, which together with the convergence of to, we pass to the limit in the problem (21), we prove that u satisfies (1), with.

4. A p(x)-polyharmonic Kirchhoff Equation

In this section, we begin by recalling some basic results on the variable exponent Lebesgue and Sobolev spaces, see details in [22] [23].

As before, we define:

(36)

where is a bounded domain, and,. Let h be the function in, an important role in manipulating the generalized Lebesgue-Sobolev spaces is played by spaces, which is the convex function: defined by:

(37)

Let p be a fixed function in. We endow the Luxemburg norm:

(38)

by variable exponent Lebesgue space, it is a separable, reflexive Banach space. For, in, then the embedding is continuous and the norm of the embedding operator does not exceed. see [23].

be the function obtained by conjugating the exponent p pointwise, so that for all, the belongs to.

Note that, by Hölder-type inequality is valid:

(39)

with as proved in [23].

For, we introduced the variable exponent Sobolev space defined by:

(40)

and endow the standard norm:

We point out that the nonstandard growth condition of type.

Lemma 4.1. (Therorems 1.3 of [24] ) If, with , then the following relations hold:

and in measure in and . In particular, is continuous in.

From now on we also assume that, where is the space of all the functions of, which are logarithmic Hölder continuous, there exists, such that:

With, the space denotes the completion of with respect to the norm.

Lemma 4.2. is a separable, uniformly convex, Banach space, see details in [22].

By the Poincaré inequality, see [25] [26], the equivalent norm for the space is given by:

(41)

under this assumption, when, as a consequence for the main Coldéron-Zygmund results, there exists a constant such that:

(42)

We recall that the operator is defined in (4) is vectorial, when s is odd, we endow space with the norm

(43)

where with abuse of the notation we use the same symbol to denote both the standard Luxemburg norm in the scalar space and the norm defined in (43) for the vectorial space.

Proposition 4.1. See [17] for all there exists, such that

(44)

We endow the space with the norm, such that

Let denote the critical variable exponent related to p defined for all, by the pointwise relation:

(45)

If for all, the Sobolev embedding is continuous and compact. If and, the embedding is continuous whenever for all, there exists such that:

Moreover, for for all (or equivalent), then is compactly embedded in, see details in [17] [22] [24] [27].

Consider problem (10) with and, such that either or. The Kirchhoff function is assumed to be continuous and to verify condition (M) given in introduction, where.

We denote the Dirchlet function:

(46)

where is given by (4).

We study problem (10) for a solution we understand:

(47)

where is the operator in (4), and is the -polyharmonic operator, in weak sense.

In order to study the solvability of problem (10), we will analyze the associated approximate problem.

(48)

We recall some basic conditions and hypothesis by (22)-(24), and exist, then.

Theorem 4.1. There is a solution to the problem (48).

Proof. We define

Observe that, by (46), and lemma 4.1 we get:

(49)

we take, so that by (M₁, M₃), there exists,

(50)

by M₂ and (49), we can get:

by the Hölder’s inequality and the Poincaré equality, then

since and, then is bounded, coercive and weakly lower semicontuous, such that has a minimizer and the Euler equation is

Moreover, such a minimizer is unique, by the strict convexity of J.

Fix, let, define to be the unique solution of the problem:

(51)

We will use the as a test in (51) we get:

by (22), (24), (50) and Hölder’s inequality, thus,

1) If, such that

2) If, such that

We take, so that the

ball of radius is invariant under s in. In order to apply the Schauder’s Fixed Point Theorem, apart from the invariant, we need to check the continuity and compactness of s as an operator from to. So, the proof will be divided into two steps.

Step 1: We prove the continuity. In order to do this, we define and then:

(52)

Since the convergence of in, by (52) we obtain:

(53)

In fact, let, be a sequence in converging to.

To this end, by choosing as a test function, we have

by the inequality for, , (22), (38) and Hölder’s inequality, we obtain:

(54)

as,

where is bounded, since (53) and g is continuous, such that

hence s is continuous from to.

Step 2. We prove S is compact, first we take a sequence that, therefore by Rellich-Kondrachov Theorem, we obtain

(55)

Since S is continuous,.

with C is a positive constant, independent of k, such that,

(56)

Because of the continuity of S, necessarily, so that proceeding as in (54), we can get

as, the first term of the left hand is vanished, then by (55) and (56)

therefore, S is compact.

Given these conditions on S, Schauder’s Fixed Point Theorem provides the existence of, such that, i.e., solves:

(57)

By Section 3, we also use as a test function, then we can obtain the sequence is bounded in, next we will use as a test function, we can get a sequence, which converges weakly in and a.e. to u with. Finally, by the dominated convergence theorem and convergence, we prove that u satisfies (10) with.

Thus, we can learn some Kirchhoff equations by the above method.

Acknowledgements

We closely thank the following instructions. It will definitely save a lot of time and expedite the process of your paper’s publication.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Kratochvil, A. and Necas, J. (1971) The Discreteness of the Spectrum of a Nonlinear Strum-Liouville Equation of Fourth Order. Commentationes Mathematicae Universitatis Carolinae, 12, 639-653.
[2]	Drabek, P. and Otani, M. (2001) Global Bifurcation Result for the p-Biharmonic Operator. Electronic Journal of Differential Equations, 2001, 1-19.
[3]	El Khalil, A., Kellati, S. and Touzani, A. (2002) On the Spectrum of the p-Biharmonic Operator. Electronic Journal of Differential Equations, 9, 161-170.
[4]	Correa, F.I.S.A. and Fijueiredo, G.M. (2006) On an Elliptic Equation of p-Kirchhoff Type via Variational Methods. Bulletin of the Australian Mathematical Society 74, 236-277. https://doi.org/10.1017/S000497270003570X
[5]	Ma, T.F. (2005) Remarks on an Elliptic Equation of Kirchhoff Type. Nonlinear Analysis, 63, 1967-1977. https://doi.org/10.1016/j.na.2005.03.021
[6]	Ma, T.F. (2005) Positive Solutions for a Nonlinear Kirchhoff Type Beam Equation. Applied Mathematics Letters, 18, 479-482. https://doi.org/10.1016/j.aml.2004.03.013
[7]	Autuori, G., Pucci, P. and Salvatori, M.C. (2009) Asymptotic Stability for Nonlinear Kirchhoff Systems. Nonlinear Analysis, 10, 889-809. https://doi.org/10.1016/j.nonrwa.2007.11.011
[8]	Villaggio, P. 1997 Mathmatical Models for Elastic Structures. Cambridge University Press, Cambridge. https://doi.org/10.1017/CBO9780511529665
[9]	Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Soriano, J.A. (2001) Global Existence and Uniform Decay Rates for the Kiechhoff-Carrier Equation with Nonlinear Dissipation. Advances in Differential Equations, 6, 701-730.
[10]	D’Ancona, P. and Spagnolo, S. (1992) Global Solvability for the Degenerate Kirchhoff Equation with Real Analytic Data. Inventiones Mathematicae, 108, 247-262. https://doi.org/10.1007/BF02100605
[11]	Dai, G. and Hao, R. (2009) Existence of Solutions for a p(x)-Kirchhoff-Type Equation. Journal of Mathematical Analysis and Applications, 359, 275-284. https://doi.org/10.1016/j.jmaa.2009.05.031
[12]	Dai, G. and Wei, J. (2010) Infinitely Many Non-Negative Solutions for a p(x)-Kirchhoff-Type Problem with Dirchlet Boundary Condition. Nonlinear Analysis: Theory, Methods & Applications, 73, 3420-3430. https://doi.org/10.1016/j.na.2010.07.029
[13]	Benilan, P., Brezis, H. and Crandall, M.G. (1975) A Semilinear Equation in L1(RN). Annali della Scuola Normale Superiore di Pisa, 2, 523-555.
[14]	Boccardo, L., Murat, F. and Puel, J.P. (1992) L∞-Estimate for Nonlinear Elliptic Partial Differential Equations and Application to an Existence Result. SIAM Journal on Mathematical Analysis, 23, 326-333. https://doi.org/10.1137/0523016
[15]	Arcoya, D. and Boccardo, L. (2015) Regularizing Effect of the Interplay between Coefficients in Some Epllitic Equations. Journal of Functional Analysis, 268, 1153-1166. https://doi.org/10.1016/j.jfa.2014.11.011
[16]	Arcoya, D. and Boccardo, L. (2017) Regularizing Effect of Lq Interplay between Coefficients in Some Epllitic Equations. Journal de Mathématiques Pures et Appliquées, 111, 106-125. https://doi.org/10.1016/j.matpur.2017.08.001
[17]	Colasuonno, F. and Pucci, P. (2011) Multiplicity of Solutions for p(x)-Polyharmonic Elliptic Kirchhoff Equations. Nonlinear Analysis, 74, 5962-5974. https://doi.org/10.1016/j.na.2011.05.073
[18]	Adams, R.A. and Fournier, J.J.F. (2003) Sobolev Spaces. In: Pure and Applied Mathematics, 2nd Edition, Springer, Amsterdam.
[19]	Gilbarg, D. and Trudinger, N. (2001) Elliptic Partial Differential Equations of Second Order. In: Classics in Mathematics, Springer, Berlin.
[20]	Gazzola, F., Grunau, H.C. and Sweers, G. (2010) Polyharmonic Boundary Problems. Positivity Preserving and Nonlinear Higher Order Elliptic Equations in Bounded Domains. In: Lecture Notes in Mathematics, Springer, Berlin. https://doi.org/10.1007/978-3-642-12245-3
[21]	Boccardo, L. and Croce, G. (2013) Elliptic Partial Differential Equations (Existence and Regularity of Distributional Solutions). De Gruyter, Berlin. https://doi.org/10.1515/9783110315424
[22]	Dinening, L., Harjulehto, P., Hasto, P. and Ruzicka, M. (2011) Lebesgue and Sobolev Speaces with Variable Exponents. In: Lecture Notes, Springer, Berlin. https://doi.org/10.1007/978-3-642-18363-8
[23]	Kovacik, O. and Rakosnik, J. (1991) On Spaces Lp(x) and W 1,p(x). Czechoslovak Mathematical Journal, 41, 592-618.
[24]	Fan, X.L. and Zhao, D. (2001) On the Spaces Lp(x) and Wm,p(x). Journal of Mathematical Analysis and Applications, 263, 424-446. https://doi.org/10.1006/jmaa.2000.7617
[25]	Harjulehto, P., Hasto, P., Koskenoja, M. and Varonen, S. (2006) The Dirchlet Energy Integral and Variable Exponents Sobolev Speaces with Zero Boundary Values, Potential Analysis, 25, 205-222. https://doi.org/10.1007/s11118-006-9023-3
[26]	Diening, L. and Ruzicka, M. (2003) Calderon-Zygmund Operators on Generalized Lebesgue Spaces Lp(·) and Problems Related to Fluid Dynamics. Journal für die reine und angewandte Mathematik, 563, 197-220. https://doi.org/10.1515/crll.2003.081
[27]	Dinening, L. (2004) Riesz Potential and Sobolev Embeddings on Generalized Lebesdue and Sobolev Speaces Lp(·) and Wk,p(·). Mathematische Nachrichten, 268, 31-43. https://doi.org/10.1002/mana.200310157