Regression Analysis of a Kind of Trapezoidal Fuzzy Numbers Based on a Shape Preserving Operator ()
1. Introduction
Fuzzy regression, one of the most popular methods of modeling and prediction, is an important statistical tool in evaluating the functional relationship between a set of explanatory variables and explained variable (Montgomery and Peck, 2006 [1] ). It shows particular advantages in analyzing complex systems where the vagueness of human subjective judgment doesn’t work, such as economic systems, social systems and environmental systems. In most fuzzy regression models, deviations between the observed and estimated values are supposed to be due to random errors, like classical linear regression model. But in the real world, imprecise information, incomplete knowledge, unacquirable data and indeterminable underlying model can lead to larger error.
Therefore, fuzzy set theory, introduced by Zadeh (1965) [2] , provides us appropriate tools for regression analysis, when relationship between variables is vaguely defined or observations are recorded imprecisely. After introducing fuzzy set theory, fuzzy regression techniques can be classified into two distinct areas. The first approach, possibilistic regression, proposed by Tanaka et al., (1982) [3] , aims at minimizing the total spread of the output. In this case, the problem of fitting a fuzzy model can be viewed as a linear programming problem. Still in this area, Tanaka and Ishibushi (1991) [4] extended their approach for dealing with interactive fuzzy parameters. In the fuzzy literature, several extensions of this approach have been proposed [5] [6] [7] [8] . Five years later, Celmins (1987) [9] and Diamond (1988) [10] put forward another approach, the fuzzy least squares regression, which aims to minimize the overall square errors between the observed and the estimated values. Hong et al. (2001) [11] studied the fuzzy least squares linear regression by using shape preserving operations. Moreover, several variants of this approach [12] [13] [14] [15] [16] have been used in fuzzy linear regression.
Both of the above approaches to fuzzy regression are widely used in usual fuzzy linear regression. But they are all sensitive to outliers. In such cases, least absolutes deviation (LAD) based on least squares deviation (LSD), is preferred to be used as a robust method. Especially, when outliers are in the response variable, the LAD estimator is more robust than the LSD estimator (Stahel and Weisberg, 1991 [17] ). Based on this method, many researchers made more extension about fuzzy linear regression models. However, each has his strong point. When there exist no outliers, LSD is similar to LAD, even better for evaluating more steady and unique solution [18] [19] [20] . Besides, Yager (1980) [21] proposed centroid method to translate fuzzy numbers into crisp numbers. Based on this, Zhang (2012) [22] proposed statistical analysis of fuzzy regression model based on centroid method.
In the development of fuzzy linear regression models, a new problem arose imperceptibly that the usual multiplication changed the shape of fuzzy numbers in some cases. On the one hand, Hojati et al. (2005) [23] proposed to evaluate the estimators of fuzzy outputs and parameters, by setting
-set in fuzzy multiplication, but the estimators of fuzzy outputs depend on the value of
, which is unknown. On the other, a shape preserving operator,
was proved, by Hong (2001) [24] , to be the only T-norm which induces a shape preserving multiplication of LL-fuzzy numbers. Mesiar (1997) [25] and Hong et al. (1997) [26] all made further study based on
, which can efficiently control the shape of estimators and decrease the risk of bias caused by taking minimum (Hong et al., 2001) [27] .
However, traditional fuzzy regression is still based on triangle fuzzy numbers or partial fuzzy numbers between inputs, coefficients, output. In consideration of that trapezoidal fuzzy numbers, which can represent other types of fuzzy numbers, take an important role in fuzzy numbers [28] [29] [30] . Some researchers made further study on fuzzy linear regression based on trapezoidal numbers [31] [32] [33] . And the distance between trapezoidal fuzzy numbers is also an important research topic in the fuzzy set theory, which is a basis for many related applications. So many researchers have investigated and obtained some meaningful conclusions [34] [35] [36] [37] . Taking advantages of LSD and trapezoidal fuzzy number and basing on the paper, written by Wang and Lu (2016) [33] , we first introduce the basic set theories, the basic arithmetic propositions of
and a new distance between trapezoidal fuzzy numbers. Then we want to propose a new model, whose coefficients are trapezoidal fuzzy numbers, basing on the shape preserving operator,
, to expand fuzzy regression, while no outliers in sample set and investigate the model algorithms and fulfil model complexity analysis.
The structure of this paper is as follows. In Section 2, we introduce some basic notions, and prove the good arithmetic property of
and our proposed distance. In Section 3, we propose fuzzy regression model based on least squares deviation with FIFCFO (fuzzy input-fuzzy coefficient-fuzzy output), investigate its steps detailedly, evaluate the performance of our model and introduce the measures of errors, such as error index, similarity measure and distance criterion. In Section 4, we use three examples to illustrate our proposed model and make comparisons with existing fuzzy regression models. In the last section, we do comprehensive analysis about our proposed model and give the results and conclusion.
2. Preliminary
For the sake of rigor and clarity, the basic fuzzy set theories and the basic arithmetic propositions of the shape preserving operator, used in this paper, will be introduced in this section. Throughout this paper, we use R to denote all the real numbers, FN stands for the set of the all fuzzy numbers in R.
Definition 1. (Zadeh, 1965 [2] ). Suppose that
is a fuzzy set in R and satisfies the following properties:
1) Regularity:
.
2) Bounded closed interval:
is a bounded closed interval.
Then we call
a fuzzy number in R.
Definition 2. (Hu, 2010 [38] ). Set
is a fuzzy number in R, if the
, then we call
a positive fuzzy number, and denote the set of all the positive fuzzy numbers in R by PFN. If the
, then we call
a negative fuzzy number, and denote the set of all the negative fuzzy numbers in R by NFN.
Definition 3. (Hu, 2010 [38] ). Suppose that the membership function of LR-type fuzzy number
is defined as follows:
(1)
where
satisfy
1)
2)
3)
4)
and
are non-increasing functions on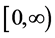 .
.
Here,
is the center point,
is the width of the left side and
is the width of the right side of the fuzzy number
, respectively.
and
. Besides, we call
a LL-fuzzy number, when
.
Suppose
a trapezoidal fuzzy number in
. If the membership function of
can be represent as that in Definition 3, then we call
a LL-trapezoidal fuzzy number and denote the set of the all LL-trapezoidal fuzzy numbers as
. Therefore, we let
, where
and
stand for the positive
and the negative
in R, respectively.
Definition 4. (Hu, 2010 [38] ). For any
, mapping 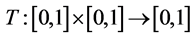 satisfies the following conditions:
satisfies the following conditions:
1) commutative law:
2) associative law:
3) monotonicity:
4) boundary condition:
.
Then we use T to denote T-norm on
.
Proposition 1. (Hu, 2010 [38] ) T is T-norm on
, it is generally acknow- ledged that
, here
(2)
 (3)
(3)
where
is called drastic product and
is called minimax operator.
Definition 5. (Hu, 2010 [38] ). Let
,
stands for the arithmetic operations on R, such as
, and
stands for its arithmetical operations on FN, such as
:
 (4)
(4)
Hence, we use  and
to stand for extended addition, extended subtraction and extended multiplication of
, respectively.
and
to stand for extended addition, extended subtraction and extended multiplication of
, respectively.
Proposition 2. Let , so we can get
, so we can get
1)
2)
(5)
3)
Proposition 3. Let
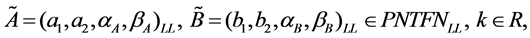
so we can get
(6)
Proof. Let
,
, and their membership function of satisfy Definition 3. We consider the case of
, which means
. Then,
1) For
,
2) For
,
3) For
,
It follows that
,
. For the other cases, we can similarly get the same formulas as the cases in (6) and omit the proof.
Remark. The propositions 1.3 in Wang (2016) [33] are the special cases of our proposition 2 and proposition 3.
Proposition 4.
is the only T-norm which can induce a shape preserving multiplication of
.
Proof. From proposition 3, we can get that
induces a shape preserving multiplication of
. The following work is to prove
is the unique one induces a shape preserving multiplication on
.
Now, give
be a non-increasing continuous function form
to
with
, which induces the case of
and assume
. Let
. Then
. For this, suppose
, for some
, then there exist
such that
,
. Then
Let
. Then by Nguyen’s theorm (1978) [39]
for
. Now suppose
for some
, and hence
. But, since
,
for any
. Then
, a contradiction. Hence
is not a fuzzy number of LL-type. Therefore, we have proved this proposition.
Proposition 5. Let
,
,
,
, so we can get
(7)
Proposition 6. Let
,
,
,
, then
 (8)
(8)
Definition 6. (Xu and Li, 2001) Set
, then the distance between
is defined as follows:
(9)
where
,
,
,
is an increasing function on
,
, and
.
Theorem 1. Set
, their membership function can be represented as the form of that in Definition 3, then the distance can be defined as follows:
(10)
where
,
,
,
.
Proof. For
, we can get the
-set of
:
so,
further, we can get
Hence, we complete the proof of Theorem 1.
In the following discussion, we set
,
, then we can get
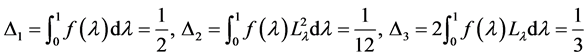
3. Fuzzy Least Squares Linear Regression Model
In this section, we consider a group of n sample data, denoted by
,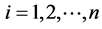 . Let
be the dependent variable, and
be the
regression coefficient,
be the random error. Here
,
. Then the general trapezoidal fuzzy linear regression model can be represented as follows:
. Let
be the dependent variable, and
be the
regression coefficient,
be the random error. Here
,
. Then the general trapezoidal fuzzy linear regression model can be represented as follows:
(11)
Now, we define set
and set
,
,
. If
, otherwise,
. Then this linear regression model has the following form (specify
). According to
, we can calculate the model:
(12)
(13)
We determine each estimated value
of the regression coefficient
based on the least squares deviation criterion by minimizing the overall square error according to the proposed square distance and obtain the following objective function:
(14)
Finally, we draw the conclusion:
(15)
Considering the efficiency of evaluation, we design the specific steps in the following. The whole process is solved by using MATLAB.
Step 1: Calculate
, the centers of
and
, with centroid method, then the estimates ,
.
,
.
Step 2: Determine set
and set
.
Step 3: Compare the sign of
and the estimates of
, if they are same, we can determine
, or we need to modify set
and set
and repeat Step 2, until the sign of
is consistent with preset.
3.1. Independent Variable, Dependent Variables and Regression Coefficients Are in
Based on the above, we can conclude least-squares regression of
model:
(16)
where,
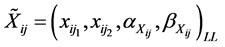 ,
,
,
,
,
,
,
,
.
Let
,
 (17)
(17)
The other cases can be calculated as the above similarly.
3.2. Error Management Criterion
For the fuzzy linear regression model (14), let
and
be the observed and estimated fuzzy response for the ith observation, respectively.
represents the difference of membership values between two membership functions,
represents the similarity of membership values between two membership functions,
represents the relative difference of membership values in shape between two membership functions,
and
are the membership functions of
and
, respectively,
and
denote the support of
and
.
1) Error Index (Kim and Bishu, 1998 [40] )
(18)
2) Similarity Measure (Rezaei et al., 2006 [41] )
(19)
3) Distance Criterion
(20)
Inspired by Chen and Hsueh (2007) [42] , we proposed
to measure the fitting effect on the shape.
For each index having its own pros and cons. In general, smaller
and
, larger
, better effect of the fitting model has. So, in this paper, we compare the fitting effect from different points.
4. Numerical Analysis
Example 1. The source sample data was produced by MATLAB randomly. First, we consider the model:
. Then, we set the true value of
,
,
,
where
,
,
,
, and
. Let
. The sample size is 50. Then, we can get the data set presented in Table 1. Now, we can use (14) to construct fuzzy regression model, obtain the estimated output and use Error Index, Similarity Measure, Distance Criterion to evaluate deviation.
From Table 2, we can find that the sum of
and
of our proposed model are smaller than that of the reference models, and the sum of
of our proposed model is larger than that of the reference models, that means our proposed model has lower deviations than the reference models.
Example 2. The source sample data comes from Table 1 in Zhang (2012) [16] , where the inputs are crisp real numbers, and the outputs are trapezoidal fuzzy numbers. In consideration of the applicability, we enlarge the sample size from 8 to 16, and expand the crisp inputs to fuzzy inputs. First, add
and corresponding
into the sample data, then expand the crisp input to fuzzy input by setting. Now, we get the final sample in data Table 3. We still use (14) to construct fuzzy regression model, obtain the estimated output and use Error Index, Similarity Measure, Distance Criterion to evaluate deviation. Besides, the results in Table 4, we also illustrate the results through Figures 1(a)-(d) (we use
to denote the observed output,
to denote Li’s estimated output,
to denote Zhang’s estimated output, and
to denote our estimated output), which represent the fitting effect of components of trapezoidal fuzzy number between observed outputs,
,
and
, respectively. In Figures 1(a)-(d), the horizontal axis represents the central value
![]()
Table 2. Comparison of the fitting effect in Example 1.
![]()
Table 4. Comparison of the fitting effect in Example 2.
of the independent variable, the vertical axis represents the value of the components of trapezoidal fuzzy number.
From Table 4, we can find that the sum of
and
of our proposed model are smaller than that of the reference models, and the sum of
of our proposed model is larger than that of the reference models, that means our proposed model has lower deviations than the reference models. From Figure 1(a) and Figure 1(c), we can see our proposed model is on par with the reference models. From Figure 1(b) and Figure 1(d), we can obviously find that the 2nd and 4th component has perfect fitting effect, they can more aptly describe the trend of the shape of output fuzzy numbers. From Figure 2, we can find the estimated outputs of our proposed model have better coverage than the reference models, especially the 1st, 3rd, 4th. In conclusion, our proposed model has better fitting effect in this case.
Example 3.The source sample data comes from Table 2 in Zhang (2012) [16] , where the inputs are crisp real numbers, and the outputs are trapezoidal fuzzy numbers. In consideration of the applicability, we modify the sample data, and expand the crisp inputs to fuzzy inputs. The specific steps are similar to Example 2. After obtaining the proper sample data in Table 5, we still use (14) to construct fuzzy regression model, obtain the estimated output and use Error Index, Similarity Measure, Distance Criterion to evaluate deviation shown in Table 6.
![]()
Figure 2. The shape of the four estimated outputs.
![]()
Table 6. Comparison of the fitting effect in Example 3.
From Table 6, we can find that the sum of
of our proposed model is smaller than that of the reference models, and the sum of
and
of our proposed model is larger than that of the reference models, that means our proposed model has lower deviations than the reference models, but bad shape estimation.
5. Conclusions
In this study, we took advantages of drastic product and classic LSD and used
to design the a kind of trapezoidal fuzzy number (
) regression model, which handles regression problem with fuzzy inputs, fuzzy coefficients and fuzzy outputs represented as
. The first two examples show great support for our model, and the last example is inferior in
. In general, our proposed model has better performance than the reference models when on outliers in sample sets, that means our proposed model is short of robust property.
Although the experimental results show that our proposed model has better performance, but the complexity of computation is still a potential problem even though it is solved to a certain extent by optimized program. The sample size or the number of variables is larger; the computation is more complex. In the future research, we will further study how to perform better when sample size is large, or there are outliers in sample sets and apply it to non-linear fuzzy regression analysis.
Acknowledgements
The authors appreciate the helpful comments of the referees on this manuscript.