Sontosh Kumar Sahani, M. Haider Ali Biswas
Mathematics Discipline, Khulna University, Khulna, Bangladesh.
DOI: 10.4236/ojmsi.2017.52010   PDF    HTML   XML   2,875 Downloads   5,919 Views   Citations

Abstract

The study of viral dynamics of HIV/AIDS has resulted in a deep understanding of host-pathogenesis of HIV infection from which numerous mathematical modeling have been derived. Most of these models are based on nonlinear ordinary differential equations. In Bangladesh, the rate of increase of HIV infection comparing with the other countries of the world is not so high. Bangladesh is still considered to be a low prevalent country in the region with prevalence < 1% among MARP (Most at risk populations). In this paper, we have presented the current situation of HIV infection in Bangladesh and also have discussed the mathematical representation of a three-compartmental HIV model with their stability analysis. We have determined the basic reproduction number and shown the local and global stability at disease free and chronic infected equilibrium points. Also we have shown that if the basic reproduction number , then HIV infection is cleared from T cell population and it converges to disease free equilibrium point. Whereas if , then HIV infection persists.

Keywords

CD⁴⁺ T Cells, Dynamical Systems, Basic Reproduction Number, Equilibrium Points, Stability Analysis

Share and Cite:

1. Introduction

HIV stands for human immunodeficiency virus. The virus attacks the immune system, and weakens our ability to fight infections and disease. HIV/AIDS pro- gresses in body slowly and its symptoms are shown after 6 - 8 years sometimes even later. At present, the most burning issue at the same time, the most dangerous phenomena is Human Immunodeficiency Virus (HIV) [1] . Since the beginning of the epidemic, more than 70 million people have been infected with the HIV virus and about 35 million people have died of HIV. Globally, 36.7 million [34.0 - 39.8 million] people were living with HIV at the end of 2015 [2] . An estimated 0.8% [0.7% - 0.9%] of adults aged 15 - 49 years worldwide are living with HIV, although the burden of the epidemic continues to vary considerably between countries and regions. Sub-Saharan Africa remains the most severely affected, with nearly 1 in every 25 adults (4.4%) living with HIV and accounting for nearly 70% of the people living with HIV worldwide [2] . Acquired Immunodeficiency Syndrome (AIDS) was first discovered in 1981, since then it has been considered as the most leading cause of mortality [3] . A detailed background and survey on HIV/AIDS is described in [4] [5] [6] [7] . HIV mainly targets CD⁴⁺ T cells. The continuous attack HIV causes the depletion of CD⁴⁺ T cells and this leads people to gradually become a victim of Acquired Immunodeficiency Syndrome (AIDS). For this reason, the count of CD⁴⁺ T cells is considered as the primary indicator of progression of HIV. In recent times, mathematical modeling has become the most powerful tool to incorporate the dynamic behaviors of infectious diseases. Mathematical modeling is basically referred to as a method of simulating real-life situations with mathematical equations to forecast their future behavior [8] . Numerous mathematical models have been developed to identify the characteristics of human immunodeficiency virus [9] [10] [11] . HIV dynamic model, a set of ordinary differential equations (ODE) that describe the interaction between HIV virus and human body cells, has been proven useful for understanding the pathogenesis of HIV infection and developing treatment strategies [12] . In this paper, we have shown the present scenario of HIV/AIDS in Bangladesh. Also we have studied a three-compartmental HIV model and investigated their stability at disease free and endemic equilibrium points.

2. Current Status of HIV Infection in Bangladesh

HIV is a worldwide curse. There is no such country where this pandemic disease does not exist. Although Bangladesh is still considered to be a low responded HIV infected country in world, the present situation indicate that the influence of this pandemic disease is gradually increasing. The main reason for this low prevalence could be the early and sustained HIV prevention programs targeting high risk groups backed by a state-of-the-art surveillance system. Another contributing protective factor could be the high rates of male circumcision. There is, however, a concentrated HIV epidemic among injecting drug users (IDU), primarily due to sharing of unclean syringes and needles. As a result, the rate of new infections is still on the rise and Bangladesh is the only country in the South Asia Region where new infections are rising [13] .

In Bangladesh, the first case of HIV was detected in 1989 [3] . Since then, it has been enhanced considerably. In 2015 (December 2014 to November 2015), the number of newly HIV infected people is 469 and the number of HIV/AIDS related death is 95. Till December 2015, there were 4143 reported cases of HIV and among them 658 died [6] . Here we show a graphical representation of HIV surveillance of Bangladesh (see Figure 1) from 1989 to 2015 (except 2008) [14] .

3. Three-Compartmental HIV Model

To generate a realistic model of T cell infection by HIV, we first need to consider the population dynamics of T cells in the absence of HIV. Our interest is to present a mathematical model of HIV infection and analyze the model. In this paper, we present a three compartmental model of HIV which has been taken from [15] . We have modified this model and added a drug efficacy parameter whose value is in the range between 0 and 1 [16] . The total population size 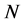is divided into three stages of HIV/AIDS progression; the susceptible population, HIV infected individuals and HIV virus 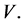The total population is given by 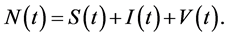The population CD⁴⁺ T cells starts with a source or production rate 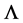and dead cells with rate are reduced from the

susceptible class. It has a logistic growth with where 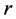is the

proliferation rate. Parameters 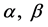and 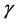are natural turnover rate of uninfected CD⁴⁺ T cells, infected CD⁴⁺ T cells and virus. Whereas 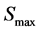is the maximum level of CD⁴⁺ T cell concentration in the body [17] . Infected CD⁴⁺ T cells it has an infection rate which is concentrated as. The transfer diagram of the model is shown in Figure 2.

Our modified model is governed by the following ordinary differential equations:

(1)

The model is positively invariant and bounded in the region

We have determined the basic reproduction number which was first introduced by Ross (1909), which is defined in epidemiological modeling as the average number of infected individuals produced by one infected immigrant in a population which is completely susceptible [18] . Finding the basic reproduction number, we can determine the endemic result of disease in populations. If, the disease vanishes and if, the disease spreads and goes to the endemic level.

Parameter Specification

If one wishes to use a mathematical model to make predictions about a particular individual or population, estimation of model parameters from data is crucial. All the parameters and their values used for model (1) are taken from [15] [16] and presented in Table 1.

4. Mathematical Analysis of Model

Here we investigate the positivity of the model, find out different equilibrium points, formulate the basic reproduction number and check the stability at disease free and endemic equilibrium points.

4.1. Positivity of the Solution

Here we check the positivity of each compartments such as susceptible cells, infected and HIV virus. We must have the positive values of these biological compartments. To test the positivity of these biological compartments, we need the following Lemma 1.

Lemma 1. Let then the solutions of the model system of equations (1) are positives.

Proof: To prove the Lemma 1, we have used the system of equations of the model (1).

in order to find the positivity we have,

(2)

Multiplying both sides of (2) by we have,

(3)

Now Integrating (3)

(4)

where is a constant. Applying the initial condition at Hence from (4),

Putting the value of into (4), we get

Hence at and. Similarly we can find the positivity of and under the initial conditions.

Therefore, it is true that,.

4.2. Disease Free Equilibrium Points

The disease free equilibrium of the above HIV model (1) can be obtained by setting

thus we have,

Since we have considered the disease free equilibrium, hence. Thus the above system reduces to,

Thus, the disease free equilibrium is

Again for the endemic equilibrium point, we find, where

.

Now we calculate the basic reproduction number at.

4.3. Basic Reproduction Number

Basic reproduction number represents the average number of secondary infection caused by a single infected T cell in an entirely susceptible T cell population, throughout its period. In order to find the basic reproduction number of the model (1), we need to identify the classes which are relevant to each other. Form the model (1), we observe that the classes and are relevant. We find the gain and losses of and respectively.

Gains to is, gains to is losses to is and losses to is Now, Matrix for the gain terms:

Since basic reproduction number is to be calculated at disease free equilibrium point, hence

Matrix for the loss terms;

Inverse of is

Now we have to evaluate a matrix such that

Hence the largest eigen value of the matrix is. Thus, the basic the reproduction number of the model (1) is. Now we check the local stability of the model (1) at disease free equilibrium point and chronic infection equilibrium point.

4.4. Local Stability of Disease Free Equilibrium Point

Firstly, we investigate the local stability at disease free equilibrium point but before that we need the following theorem.

Theorem 1: If, the disease free equilibrium point of system (1) is locally asymptotically stable. If, is locally stable and if, then is unstable.

Proof: To prove the above theorem, the following variation matrix is computed corresponding to equilibrium point. From the model (1), let

then the system (1) reduces to,

The Jacobian Matrix of the system (1) is

(5)

at, Equation (5) becomes

Now we have to find out the characteristic equation. To do that, first we have to calculate where, is a scalar and is identity matrix. Let, then

To find out the characteristic equation we need to perform, hence

Thus, the characteristic equation is

where

We observe that, first root of the characteristic equation is

If, then. Also,. Again, hence by Routh-Hurwitz criteria [19] , locally asymptotically stable. If, then and becomes locally stable. If, then and becomes unstable. Now we investigate the local stability of endemic equilibrium point.

4.5. Local Stability of Chronic Infection Equilibrium Point

Now we investigate the local stability of chronic infection equilibrium point. We need the following Lemma 2.

Lemma 2: Let be a real matrix. If and are all negative, then all of the eigen values of have negative real part [20] .

Before we apply the Lemma 2, we need the following definition of second additive compound matrix.

Definition 1: Let be an real matrix. The second additive compound matrix of is the matrix defined as follows [21] [22] :

Theorem 2: The chronic infection equilibrium point of the system (1) is locally asymptotically stable if.

Proof: From Equation (5), we have

at chronic infection equilibrium point,

where.

Now the second additive compound matrix is

(6)

Now we compute respectively. Hence

,

Hence by Lemma 2, is locally asymptotically stable.

5. Numerical Simulations

We have discussed the locally asymptotically stability of both infection free equilibrium and chronic infection equilibrium above. When, the endemic equilibrium may only be stable for small or large. Our numerical solutions consistently show the existence of periodic solutions when is unstable. For the numerical result we use the parametric values used in Table 1 taken from [15] and [16] but with the variation of. Considering, we have shown local stability of both the healthy CD⁴⁺ T cells and HIV virus at and (see in Figure 3 and Figure 4). Whereas at, is unstable and a periodic solution exists (see in Figure 5).

We observe is unstable within the range of between 0.093453 and 1.9118. From Figure 4, we observe viral load 600 mm⁻³ persists when while it is below 100 mm⁻³ at. Again when the initial oscillation disappears after 145+ days whereas at the damped oscillation are clearly visible after 2000 days. We also note that, the values of in these three cases are 0.5081, 0.8227 and 0.48431 respectively.

6. Conclusion

Bangladesh government and several NGO’s have played a magnificent role in keeping the HIV prevalence low by enhancing awareness to people. But this low prevalence rate is increasing day by day and becoming a great threat to us. In this paper, we have shown a brief report of HIV/AIDS of Bangladesh from 1989 to 2014 (except 2008). Again we have discussed the mathematical presentation of HIV infection in a three-compartmental model. In the model, we added a probability term with the infected T cells. Then we have calculated the basic re-

production number, where is considered as equilibrium of

CD⁴⁺ T cells in the absence of HIV infection. At disease free equilibrium point, the model is assumed to be stable and later we conclude the stable and unstable condition for the chronic infected equilibrium points. With the proliferation term and reproduction number, we find the solution of it. We find the numerical solution at different equilibrium points and have observed the curve in periodic and damped oscillation.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Biswas, M.H.A. (2012) Optimal Chemotherapeutic Strategy for HIV Infections-State Constrained Case. Proceedings of the 1st PhD Students Conference in Electrical and Computer Engineering, University of Porto, Porto, 28-29 June 2012.
[2]	WHO Report on HIV/AIDS, Asia-Pacific Region, World Health Organization, Geneva, Switzerland, 2016.
[3]	Biswas, M.H.A. (2014) On the Evolution of AIDS/HIV Treatment: An Optimal Control Approach. Current HIV Research, 12, 1-12. https://doi.org/10.2174/1570162X1201140716094638
[4]	Biswas, M.H.A. (2013) Necessary Conditions for Optimal Control Problems with State Constraints: Theory and Applications. PhD Thesis, University of Porto, Porto.
[5]	Biswas, M.H.A. (2012) AIDS Epidemic Worldwide and the Millennium Development Strategies: A Light for Lives. HIV and AIDS Review, 11, 87-94. https://doi.org/10.1016/j.hivar.2012.08.004
[6]	Biswas, M.H.A. (2013) On the Immunotherapy of HIV Infections via Optimal Control with Constraint. Proceedings of the 18th International Mathematics Conference, Dhaka, 20-22 March 2014, 51-54.
[7]	Biswas, M.H.A. (2012) Model and Control Strategy of the Deadly Nipah Virus (NiV) Infections in Bangladesh. Research & Reviews in Biosciences, 6, 370-377.
[8]	Biswas, M.H.A., Paiva, L.T. and de Pinho, M.D.R. (2014) A SEIR Model for Control of Infectious Diseases with Constraints. Mathematical Biosciences and Engineering, 11, 761-784. https://doi.org/10.3934/mbe.2014.11.761
[9]	Banks, H.T. and Bortz, D.M. (2002) A Parameter Sensitivity Methodology in the Context of HIV Delay Equation Models. Center for Research in Scientific Computation Box 8205, North Carolina State University, Raleigh, NC.
[10]	Coppel, W.A. (1995) Stability and Asymptotic Behavior of Differential Equations, Health, Boston.
[11]	Mukandavire, Z., Das, P., Chiyaka, C. and Nyabadza, F. (2010) Global Analysis of an HIV/AIDS Epidemic Model. World Journal of Modeling and Simulation, 6, 231-240.
[12]	Duffinin, R.P. and Tullis, R.H. (2002) Mathematical Models of the Complete Course of HIV Infection and AIDS. Journal of Theoretical Medicine, 4, 215-221. https://doi.org/10.1080/1027366021000051772
[13]	The World Bank, HIV/AIDS in Bangladesh.
[14]	National AIDS/STD Program, Bangladesh.
[15]	Wang, L. and Li, M.Y. (2006) Mathematical Analysis of the Global Dynamics of a Model for HIV Infection of CD4+ T Cells. Mathematical Biosciences, 200, 44-57. https://doi.org/10.1016/j.mbs.2005.12.026
[16]	Adams, B.M., Banks, H.T., Davidiana, M., Kwon, H.D., Tran, H.T., Wynne, S.N. and Rosenberg, E.S. (2004) HIV Dynamics Modeling, Data Analysis and Optimal Treatment Protocols. Journal of Computational and Applied Mathematics, 184, 10-49. https://doi.org/10.1016/j.cam.2005.02.004
[17]	Perelson, A.S. and Nelson, P.W. (1999) Mathematical Analysis of HIV-1 Dynamics in Vivo. SIAM Review, 41, 3-44. https://doi.org/10.1137/S0036144598335107
[18]	Callaway, D.S. and Perelson, A.S. (2001) HIV-1 Infection and Low Steady State Viral Loads. Bulletin of Mathematical Biology, 64, 29-64. https://doi.org/10.1006/bulm.2001.0266
[19]	Gantmacher, F.R. (1959) Applications of the Theory of Matrices. Interscience, 641, 1-8.
[20]	Cai, L., Li, X., Ghosh, M. and Guo, B. (2009) Stability Analysis of an HIV/AIDS Epidemic Model with Treatment. Journal of Computational and Applied Mathematics, 229, 313-323. https://doi.org/10.1016/j.cam.2008.10.067
[21]	Gupta, K.P. (2007) Topology. 16th Edition, Pragati Prakashan, Meerut.
[22]	Ross, S.L. (2004) Differential Equations. 3rd Edition, John Wiley & Sons Inc., Hobo-ken. https://doi.org/10.1007/978-1-4757-3949-7