Experimental Design Approach with Response Surface Methodology for Removal of Indigo Dye by Electrocoagulation ()
1. Introduction
Textile dyes are usually used in excess, especially when they belong to the disperse dye class: this class groups, indeed, organic non-ionic compounds nearly insoluble, applied in aqueous solution using a simple immersion technique, which induces large water consumption [1] . Consequently, up to 40% of the amount of dyes is not fixed to textile fibres [2] . Residual dyestuffs in textile wastewaters present the disadvantage to exhibit simultaneously a high toxicity level and a poor biodegradability with an aesthetic pollution which has a strong psychological effect [3] . As dyestuffs are visible at low concentrations, aesthetic standards are often more difficult to meet than legal standards.
In recent years, investigations have been focused on the treatment of wastewaters using electrocoagulation (EC). The electrocoagulation has successfully been used for the treatment of wastewaters such as electroplating wastewater [4] , laundry wastewater [5] , latex particles [6] , restaurant wastewater [7] and slaughterhouse wastewater [8] . Meanwhile, electrocoagulation process has been widely used in the removal of arsenic [9] , phosphate [10] , sulfide, sulfate and sulfite [11] and boron [12] . Treatments of waste- waters containing textile dyes have been studied by electrocoagulation method. The results of these studies show that Chemical Oxygen Demand (COD), color, turbidity and dissolved solids at varying operating conditions are considerably removed [13] [14] .
In this study, the aim is to demonstrate that such reactors can be used as electrocoagulation cell for studying effects of different parameters like applied current density, initial concentration of dye, conductivity in the aim to investigate dye removal and in order to determine desired operating conditions. Operating cost for the removal of dye was calculated. In the calculation of the operating cost, only material and energy costs were considered.
2. Materials and Methods
2.1. Conventional Reduction of Indigo
As a vat dye indigo needs to be reduced to its water-soluble form before it can be used in dyeing. The reduction of indigo to leuco-indigo, represents an important type of industrial process which is operated worldwide on a considerable scale [15] .
The indigo (BEZEMA AG, Switzerland) reduction is industrially done, in the SITEX (Textile Industrial Company-Ksar Hellal, Tunisia), with Sodium dithionite (Fluka, Germany) as a conventional reducing agent. It is also known as sodium hydrosulphite, or Hydro (Na2S2O4) and has been a major reducing agent [16] in the industrial reduction of vat dyes including indigo due to its chemical as well as economic advantages. It is used with all vat dyes at temperatures ranging up from 30˚C [17] .
Indigo is reduced by Sodium Hydroxide, and then the obtained form Leuco is filtered through a sieve of 23 µm to remove fibers. Afterwards, we transfer the filtrate to the electrochemical processing cell.
2.2. Cell Electrochemical Reactor
The electrochemical reactor was a 16.957 L acrylic column with a height of 60 cm and a diameter of 9.54 cm. It contained a set of one pair of electrodes made of aluminum. Dimensions of each electrode were 335 mm × 130 mm × 2 mm so, its total area (S) was 0.088960 m2 and the distance between two electrodes in electrochemical cell was 7 mm in all experiments (Figure 1). The electrodes were connected to a DC power supply (Laboratory DC. Power supply Model M10-SP600 SL) with galvanostatic operational options for controlling the current density.
All the runs were performed at room temperature. In each run, 30 ml of the dye solution was filtered by Whatman® glass microfiber filters (7 µm). The filtrate obtained was collected for the analysis of water properties and the electrodes were well polished by sandpaper before each test. All experiments were repeated twice, and the experimental error was 3%.
During the runs, the solution in the reactor unit was stirred at 2 rpm by a magnetic stirrer. The experiments were carried out in a batch mode with a liquid sample of 13.71 L. Different current intensities were applied (0.5 to 1.5A).
The conductivity measurement was performed with a conductimeter (HANNA Instruments). The pH of the solutions was measured by a pH meter (370 pH Meter JENWAY) and adjusted by adding NaOH or H2SO4 (Merck, Germany) solutions. The batch experimental cell is shown in Figure 1. The conductivity of solutions was raised up and adjusted in different values by the addition of NaCl (1 g/L to 6 g/L).
The commercial dyes indigo used in this project were furnished by SITEX. Dye solutions were prepared by dissolving dyes in distilled water and reduced by sodium hydrosulfite under the conditions described above. In the present experimental study, aluminum has been used as elecrodes and the treatment time fixed at 25 min.
2.3. Determining the Characteristic Decolorization of Indigo Dye
2.3.1. Absorbance Characteristics
The dye concentrations were determined from their absorbance characteristics in the UV-VIS range (200 - 800 nm) with the calibration method. HACH Lange DR 3900 spectrophotometer was used. For these measurements, the maximum absorption (λmax = 612 nm) wavelength of dyes was determined by measuring their absorbance. The cal- culation of color removal efficiency after electrocoagulation treatment was performed using this formula (Equation (1)) [18] :
![]()
Figure 1. Apparatus of the electrocoagulation bench scale reactor: 1-Electrochemical cell; 2- Anode (Aluminum); 3-Cathode (Aluminum); 4-DC Power supply; 5-Magnetic stirring; 6-Mag- netic stirrer. (a) Schematic mounting of the electrochemical cell; (b) Experimental pilot plant of the electrochemical cell.
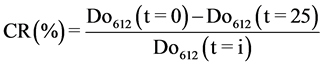 (1)
(1)
where:
Do612 (t = 0): measuring the absorbance at 612 nm at initial instant;
Do612 (t = i): measuring the absorbance at 612 nm after a 25 min, time.
2.3.2. Current Density
The current density (CD) is the important parameter for controlling the electrochemical reaction rate. CD can be formulated as:
The current density (CD) was calculated through the equation as follows (Equation (2)):
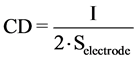 (2)
(2)
where CD is the current density (A∙m−2), I is the current (A) and S is surface area of the electrode (m2) [19] .
2.3.3. Energy Consumption
Electrical energy consumption and current efficiency are very important economical parameters in electrocoagulation process and calculated using the commonly used Equation (3) [20] :
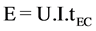 (3)
(3)
where E is the electrical energy in kWh, U the cell voltage in volt (V), I the current in ampere (A) and tEC is the time of electrocoagulation process in hours.
The electrical energy consumption (EEC, kWh/m3) has been calculated with Equation (4) [20] :
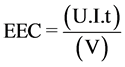 (4)
(4)
The electrodes consumption (EMC) has been calculated with Equation (5) [20] :
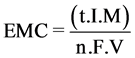 (5)
(5)
Wher’s V is the volume of the treated water (m3), “n” number of electrons in oxidation/reduction reaction (n = 3), Faraday constant (F = 96.487 C/mol), Molecular weight of the Aluminum (g/mol).
2.3.4. Operation Cost
It is well-known that the performance of an electrically driven process like electrocoagulation is dependent on electrical energy consumption which directly affects the operating cost of the process. For electrocoagulation process the operating cost includes material, mainly electrodes and electrical energy costs, as well as labor, maintenance, sludge dewatering and disposal. In this preliminary economic investigation, energy and electrode material costs have been taken into account as major cost items in the calculation of the operating cost (US$/m3 of dye solution) (Equation (6)).
 (6)
(6)
where, OC = Operating cost of water treatment (US$/m3 of waste water), EEC = electrical energy consumption (KWh/m3 of waste water), EMC = Electrode consumption (kg/m3 of waste water), a = industrial electrical energy price in Tunisia (US$/kWh) and b = wholesale electrode material price in Tunisia (US$/kg Al) for 2015 [20] .
2.4. Response Surface Methodology (RSM)
The Box-Behnken design (BBD), an experimental design for Response Surface Methodology (RSM) is a useful statistical tool for the optimization of different processes and widely used for experimental design. In this method, the leading objective is to optimize the response surface that is influenced by different parameters. RSM also identified the relationship between the controllable input parameters and the response variable [21] . It is usually applied following a screening study to explore the region of interest of the factors identified by the preceding study [22] .
3. Results & Discussion
The factors considered in this study are: NaCl concentration (g/l), Current Intensity (A) (or CD: Current Density) and initial concentration of dye (mg/l) whereas the experimental result or the response to treat is the removed dye (CR(%)).
The Response Surface Methodology (RSM) as used experimental design the Box- Behnken, to determine the optimal experimental conditions for maximum color removal, minimum energy and electrode consumption, whose objective in view the minimization of the operation cost (OC) minimum.
3.1. Response Regression Equation
The general behaviour of some phenomena in electrocoagulation can be simulated by a mathematical equation: this equation represents the regression model. Response surface methods are used to examine the relationship between one or more response variables and a set of quantitative experimental variables or factors [23] . The factors considered in this study are: initial concentration of dye (12.310, 21.155 and 31.540 mg/l), NaCl concentration (1, 3.5 and 6 g/l) and current intensity (0.5, 1, 1.5 Ampere) (Table 1), where, the experimental result or the response to treat is the Color Removal (%).
There are many types of equations that can give a good correlation between parameters, but the choice of which one should be used is dependent of the R2 value of each model. The most appropriate regression model obtained for the response (CR(%)) is the following:
Equation I: a quadratic equation with interactions for CR(%) in Equation (7):
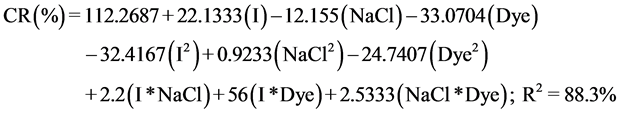 (7)
(7)
![]()
Table 1. Experimental range and levels of independent process variables.
The results were analysed using the software Minitab 14 [24] [25] . Minitab, offers a collection of software, support materials and services that enables to manage and improve the quality of processes [26] [27] . Response Surface Methods are used to examine the relationship between one or more response variables and a set of quantitative experimental variables or factors.
The regression equation of the removed dye (CR(%)), it was found that the squared multiple correlation coefficient “R2” is equal, to 88.3%; so, we can probably assume that the models may be predictable, that can give a good correlation between parameters and responses.
We can concluded from the coefficients of the equations that current intensity and color concentration coefficients are the most important terms affecting the response value (RC(%)). To validate our experimental data, we used the statistical models: ANOVA.
A.R. Amani-Ghadim et al. (2013) studied the performance of aluminum anodes for removal of the C.I. Reactive Red 43 dye from aqueous solution. They modeled the decolorization by response surface methodology. The effects of four important operational parameters including current density, electrolysis time, pH and chloride concentration were evaluated by the response surface methodology. This study showed a high correlation coefficient (R2 = 93.4) between experimental and predicted removal efficiencies. Furthermore the regression equation proved that the initial pH and the current density were the most important factors.
3.2. Variance Analysis (ANOVA)
The analysis ANOVA of the regression equations stated above is performed in order to determine the good correlation between parameters and responses. The evaluation was based on the p-value obtained. Analysis of variance is similar to the regression in that it is used to investigate and model the relationship between a response variable and one or more independent variables [27] .
The P-value related to the F-value could be used to show whether the F-value is large enough or not. In other words, P-values lower than 0.01 (at the significance level of 95%) confirm that the regression model is statistically significant [28] . The model developed of regression for CR(%) given the P-values were much lower than 0.01. In this case, the related P-value is lower than 0.01, the regression will adequately be significant as the ANOVA results indicated. On the other hand, the sum of squares (SS) related to Residual Error is very less as compared to the total sum of squares. This confirms our hypothesis (Table 2).
Takes account of all considerations, we can assume, that a second order polynomial model with interaction allows properly explain the phenomenon studied for CR(%).
3.3. Contour Plot
Based on the results Response Surface Regression and Analysis of Variance (ANOVA), as concluded, that current density and initial concentration of dye were the most important factors in electrocoagulation process for response (CR(%)).
Figure 2 shows that, when the decrease of current intensity with increase of color concentration was not suitable for the color removal. On the other hand, the effect of
![]()
Table 2. Analysis of variance for the removal color (CR(%)).
![]()
Figure 2. Contour plots of CR(%), for two most significant factors (color concentrations expressed by the absorbance value at 612 nm (a.u)) and current intensity (I).
the increase of current intensity until to 1.25 A with decrease of color concentration was suitable for color removal. But the response of CR(%) decease wen the current intensity as higher than 1.25 A and the dye concentration was less than 13.85 mg/l.
3.4. Interactions Plot
An interaction between factors occurs when the change in response from the low level to the high level of one factor is different from the change in response at the same two levels of a second factor. In other words, binary interactions between factors presented statistically significant effect, which signifies that the effect of one independent factor on the response depends upon the other factor. Interactions plots could be used to compare the relative strength of the effects across factors.
The analysis of the interactions between the experimental factors studied is shown in Figure 3. The interaction between different factors is obvious for the color removed (CR(%)).
3.5. Response Optimization
A comparison for optimum conditions between predicted and experimental responses using Box-Behnken Design is given below:
The performance of all design and response variables are shown in Figure 4, where the best optimization is approached by an overall desirability of 0.75892 at optimum operating conditions of reaction time at 25 min, current density at 0.50 A, initial color concentration at 13 mg/l and NaCl concentration at 2.67 g/l. In these conditions, the Minitab Software gives respectively, a decolorization value for Indigo dye of 86.9783% and for Operating Cost OC = 0.0007378 US$/m3. When these conditions were applied experimentally, we obtained respectively CR(%) = 85.33% and OC = 0.000558 US$/m3.
Thus, when the experimental conditions proposed by Minitab were applied to our experimentation, the values of the responses obtained are almost equal to the values obtained by calculating. Hence our models are globally validated.
![]()
Figure 3. Analysis of interaction Plots of the Color Removed (CR(%), (where: “Dye: a.u; NaCl: g/l; I: A”).
![]()
Figure 4. Response optimization of color removal (CR%), Electrical Energy Consumption (EEC) and Electrodes Consumption (EMC).
A.R. Amani-Ghadima et al. (2013) obtained, when using electrocoagulation process with aluminum anodes, a maximum removal efficiency equal to 98.90 of the C.I. Reactive Red 43 dye from aqueous solution. They achieved using the experimental optimum values of each studied factor, which was in a good conformity with the predicted values (99.99%).
4. Conclusions
Electrocoagulation was used to remove Indigo dye (leuco form), reduced in the industrial conditions of the SITEX. The effects of various operational parameters on dye removal efficiency were investigated. In this study, experimental conditions were optimized by observing the effects of interactions among the variables on color removal efficiencies CR(%), using a response surface methodology (RSM). The RSM results demonstrated significant effects of two operating variables. Initial concentration of dye and current intensity were the most important factors in electrocoagulation, as well as their interactive effects. Box-Behnken design (BBD) was used to determine the optimal removal efficiency and operation cost.
High R2 value of 88.3% for color removal, through ANOVA, verified that the accuracy of the proposed second-order regression model is acceptable. The maximum predicted and experimental color removal were 86.98% and 85.33% respectively, using optimized conditions of the current intensity (0.50 A), initial concentration of dye (12.31 mg/l) and NaCl concentration (2.67 g/l).
The optimized data for the economical removal of color at pH 8, inter electrodes distance of 7 mm, electrolysis time of 25 min and NaCl concentration of 2.67 g/l, were respectively 0.0007378 US$/m3 and 0.000558 US$/m3 for predicted and experimental values.
The optimal experimental values for the studied factors were in close agreement with those given by the model predictions (High R2 values and low P values). Our results imply that the Response Surface Methodology (RSM) with a Box-Behnken design (BBD) could be used to identify the most significant operating factors for decolorization of Indigo dye in the textile industrial wastewater during an electrocoagulation reaction.
NOTES

*N.B: This project is in the framework of a doctoral thesis MOBIDOC-PASRI the program financed by the EU and managed by the ANPR (National Agency for Promotion of Scientific Research as at Support Unit Support Program for Research and Innovation System (PASRI)).