S. Fujita¹, A. Suzuki², Y. Takato^3
1Department of Physics, University at Buffalo, State University of New York, Buffalo, NY, USA.
²Department of Physics, Faculty of Science, Tokyo University of Science, Tokyo, Japan.
³Okinawa Institute of Science and Technology Graduate University, Okinawa, Japan.
DOI: 10.4236/jmp.2016.712141   PDF    HTML   XML   1,811 Downloads   2,921 Views   Citations

Abstract

A quantum statistical theory of the superconductivity in MgB₂ is developed regarding it as a member of the graphite intercalation compound. The superconducting temperature T_c for MgB₂, C₈K ≡ KC₈, CaC₆, are 39 K, 0.6 K, 11.5 K, respectively. The differences arise from the lattice structures. In the plane perpendicular to the c-axis, B’s form a honeycomb lattice with the nearest neighbour distance while Mg’s form a base-hexagonal lattice with the nearest neighbour distance above and below the B-plane distanced by . The more compact B-plane becomes superconducting due to the electron-phonon attraction. Starting with the generalized Bardeen- Cooper-Schrieffer (BCS) Hamiltonian and solving the generalized Cooper equation, we obtain a linear dispersion relation for moving Cooper pairs. The superconducting temperature T_c identified as the Bose-Einstein condensation temperature of the Cooper pairs in two dimensions is given by , where is the Cooper pair density, the Boltzmann constant. The lattices of KC₈ and CaC₆ are clearly specified.

Keywords

Crystal Structure, BCS Hamiltonian, Electron-Phonon Interaction, Cooper Pairs, Bose-Einstein Condensation, Superconductivity

Share and Cite:

Received 30 June 2016; accepted 28 August 2016; published 31 August 2016

1. Introduction

Nagamatsu et al. [1] reported in 2001 superconductivity at 39 K in magnesium diboride MgB₂. MgB₂ forms a lattice closely related to that of a graphite intercalation compound (GIC). It is similar to NaC₂ composition- wise, but the lattice structures are distinct as shown below. The superconducting temperatures 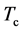of MgB₂ and NaC₂ are 39 K and 5 K, respectively. This difference arises from the lattice structures. Canfield and Crabtree [2] wrote a comprehensive review in Physics Today (2003). From the isotope effect study [2] [3] they concluded that the B-plane contains a honeycomb lattice which becomes superconducting at 0 K, while the Mg-plane is base-hexagonal and is metallic. Their conjectured lattice structure of MgB₂ is shown in Ref. 2, Figure 3. The superconducting state occurs at 0 K, where the entropy of an electron-phonon system vanishes. The third law of the thermodynamics applies. The crystal must be specified with the location of all atoms. Ref. 2, Figure 3 contains only the B-lattice and Mg-lattice with unspecifyed lattice constants. We must specify lattice systems with basic lattice units with the lattice constants. A currently presumed lattice for MgB₂ [4] is a fully intercalated graphite compound similar to that in NaC₂. We propose a different lattice. The two lattices have the same first neighbour configurations but different second nearest neighbours. Our proposed lattice has a lower Coulomb energy and should be realized in practice.

We shall develop a quantum statistical theory of the superconductivity in MgB₂, starting with a generalized Bardeen-Cooper-Schrieffer (BCS) Hamiltonian [5] and calculateing everything using the standard quantum statistical methods. Canfield-Crabtree’s and our lattices have nearly the same energies if the first neighbour configurations are examined. The second neighbour confi- gurations are different. Each B⁺ in our lattice is surrounded by six Mg⁺’s while each B⁺ in Canfield-Crabtree’s lattice is surrounded by three Mg⁺. Hence our lattice is more stable. In the course of the development, we clearly specify the lattices of C₈K º KC₈ and CaC₆.

2. Electron Dynamics

Following Ashcroft and Mermin (AM) [6] , we assume that “electrons” and “holes” in solids run as wave packets (not point-particles). We adopt the semiclassical model of electron dynamics in solids [6] . It is necessary to introduce a k-vector:

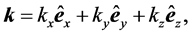(1)

where, , 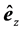are the orthonormal vectors, since the k-vectors are involved in the semiclassical equation of motion:

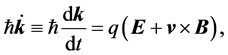(2)

where 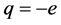is the electron charge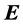, and and are the electric and magnetic fields, respectively. The vector

(3)

is the electron velocity, where is the energy.

If the electron is in a continuous energy range (energy band), then it will be accelerated by the electric force, and the material is a conductor. If the electron’s energy is in a forbidden band (energy gap), it does not move under a small electric force, and the material is insulator. If the acceleration occurs only for a mean free time (inverse of scattering frequency), the conductivity for a simple metal is given by Drude’s formula [6] :

(4)

where n is the electron density and the effective mass.

We consider a graphene which forms a 2D honeycomb lattice. The Wigner-Seitz (WS) unit cell, a rhombus, contains two C’s. We showed in our earlier work [7] [8] that graphene has “electrons” and “holes” based on the rectangular unit cell. We briefly review our calculations below. We assume that the “electron” (“hole”) wave packet has the charge () and a size of the rectangular unit cell, generated above (below) the Fermi energy. We showed [7] earlier that a) the “electron” and “hole” have different charge distributions and different effective masses; b) that the “electrons” and “holes” move in different easy channels; c) that the “electrons” and “holes” are thermally excited with different activation energies, and d) that the “electron” activation energy is smaller than the “hole” activation energy:

(5)

Hence, “electrons” are the majority carriers in graphene. The thermally activated electron densities are given by

(6)

where and 2 represent the “electron” and “hole”, respectively.

3. Lattice Structures in C₈K = KC₈, CaC₆ and MgB₂

Graphite is composed of graphene layers stacked in the manner ABAB∙∙∙ along the c-axis. We may choose an orthogonal unit cell shown in Figure 1.

The carbons (circles) in the A (B) planes are shown in dark (light) gray circles.

The unit cell contains 16 C’s. The two rectangles (white solid lines) are stacked vertically with the interlayer separation, Å, much greater than the nearest neighbour distance between two C’s, Å:

(7)

The unit cell has three side-lengths:

(8)

Clearly, the system is periodic along the orthogonal directions with the three periods given in Equation (8). Hence, the system can be considered as orthorhombic with the sides, , ,.

The negatively charged “electron” (with the charge) in graphite are welcomed by the positively charged C⁺ when moving vertically up or down in the plane. Then, the easy direction for the “electrons” is vertical. The easy direction for the “holes” is horizontal. There are no hindering hills for “holes” moving horizontally. Hence, the “electron” in graphite has the lower activation energy than the “hole”:. Then, “electrons” are the majority carriers in graphite. The thermoelectric power (Seebeck coefficient) measurements by Kang et al. [9] show that the majority carriers in graphite are “electrons” in agreement with our theory.

We now consider GIC. Let us first take C₈K. The K⁺ ions should enter as interstitials and occupy the sites away from the positive ions C⁺. We see in Figure 1 that the center of the unit cell is empty. Each K⁺ should occupy the midpoint between two graphene layers. The 3D unit cell contains 16 C’s and 2 K’s. Alkali metal GIC, including C₈Li, C₈Rb, should form similar lattices. Next we condier C₆Ca. Carbons (C) in graphite form a honeycomb lattice in the A plane as shown in Figure 1. There are eight (8) C’s and four (4) hexagon centers, (two full circles, two half-circles and four quarter-circles). If we fill the hexagon centers with C’s, then we obtain twelve (12) C’s in the 2D unit cell. Similarly the configuration of the B-plane and that one below is prescribed. There are 2 × 12 C’s in the planes A and B, and 2 × 2 Ca’s between the planes for C₆Ca. The composition ratio 6:1 is correct. After the C-filling, the C-plane becomes primitive (base)-hexagonal and has a 60˚ rotation symmetry. The primitive unit cell contains six (6) C’s. Two Ca’s are likely to occupy below the centers of the primitive cells located at the two-light gray circles in Figure 1. A real 3D C₆Ca is obtained by stacking the C₆Ca sheets in the manner ABAB… We note that the structure of C₆Ca is significantly more compact than that of C₈K. C₆Yb should have a similar lattice structure. GIC C₄Na (C₃K, C₂Na) should have the same 12 C-sheets and 3 Na (4 K, 6 Na) intersheets.

Consider now MgB₂. It is only natural to start with the B-plane since this plane becomes superconducting at 0 K. Let us look at the top sheet in Figure 1. Within the white rectangle, there are eight (8) balls and four (4) vacant hexagons. If B’s occupy the ball sites and Mg’s occupy the hexagon-centers sites in the neighbour sheet above (or below), then we obtain the most likely lattice. The composition ratio 2:1 is correct. The B-plane contains a honeycomb lattice with a nearest neighbour distance with a 120˚ rotation symmetry. The Mg-plane contains a base-hexagonal lattice with the nearest neighbour distance. Crystals Mg and B are known divalent and trivalent hexagonal metals [6] . Since the B-plane in MgB₂ is more compact with the smaller lattice constant, the B-plane is likely to become superconducting at the lowest temperatures. Note that all ions position are specified. Ions Mg⁺ and B⁺ are positively charged so that they tend to stay away among and between them.

Our lattice and Canfield-Crabtree’s are different in the second nearest neighbour configuration. Each B⁺ in our lattice is surrounded by six Mg⁺ while each B⁺ in Canfield-Crabtree’s lattice is surrounded by three Mg⁺. Hence our lattice is more stable. The B-plane contains a honeycomb lattice of B's for both. Our Mg-plane contains a base-hexagonal lattice of the nearest neighbour distance. In summary we found that a) the B-honeycomb lattice has smaller nearest neighbour distance than the Mg hexagonal lattice with the nearest neighbour distance. The more compact means the higher conduction electron density; b) The centers of mass (CM) of hexagons are displaced upward by a short distance to take advantage of the smaller repulsive Coulomb energy. There is a mismatch between the B-plane and the Mg-plane centers, a unique feature for MgB₂.

4. The Hamiltonian

The countability and statistics of the fluxons (magnetic flux quanta) are the fundamental particle properties. We postulate that the fluxon is a half-spin fermion with zero mass and zero charge.

We assume that the magnetic field is applied perpendicular to the graphene plane. The 2D Landau level energy,

(9)

with the states, , have a great degeneracy (no -dependence). The is the effective mass of an “electron”. Following Zhang, Hansson and Kivelson [10] , we introduce composite (c-) particles. The Center-of-Mass (CM) of any c-particle moves as a fermion or a boson. That is, the eigenvalues of the CM momentum are limited to 0 or 1 (unlimited) if the composite contains an odd (even) number of elementary fermions. This rule is known as the Ehrenfest-Oppenheimer-Bethe’s (EOB’s) rule [11] . Hence the CM motion of the composite containing an electron and Q fluxons is bosonic (fermionic) if Q is odd (even). The system of the c-bosons condenses below some critical temperature and exhibits a superconducting state while the system of c-fermions shows a Fermi liquid behavior.

A longitudinal phonon, acoustic or optical, generates a charge density wave, which affects the electron (fluxon) motion through the charge displacement (current). Let us first consider the case of superconductivity. The phonon exchange between two electrons shown in Figure 2 generates a transition in the electron states with the effective interaction

(10)

where is the electron energy, the phonon energy, and the electron-phonon interaction strength.

An electric current loop generates a magnetic field (flux) while a magnetic flux is surrounded by diamagnetic currents. Thus the currents and the magnetic field are coupled. The exchange of a phonon between an electron and a fluxon also generates a transition in the electron states with the effective interaction:

(11)

where is the fluxon-phonon (electron-phonon) interaction constant. The Landau oscillator quantum number is omitted; the bold denotes the momentum and the italic the magnitude. There are two processes, one with the absorption of a phonon with momentum and the other with the emission of a phonon with momentum, see Figure 3(a) and Figure 3(b), which contribute to the effective

interaction with the energy denominators and, generating Equation

(11). The interaction is attractive (negative) and most effective when the states before and after the exchange have the same energy as for the degenerate 2D LL.

BCS [5] assumed the existence of Cooper pairs [12] in a superconductor, and wrote down a Hamiltonian containing the “electron” and “hole” kinetic energies and the pairing interaction Hamiltonian with the phonon variables eliminated. We start with a BCS-like Hamiltonian for the QHE: [13]

(12)

where is the number operator for the “electron” (1) (“hole” (2), fluxon (3)) at momentum and spin s with the energy, with annihilation (creation) operators c () satisfying the Fermi anti- commutation rules:

(13)

The fluxon number operator is represented by with a () satisfying the anti-commutation rules:

(14)

The phonon exchange can create electron-fluxon composites, bosonic or fermionic, depending on the number of fluxons. The CM of any composite moves as a fermion (boson) if it contains an odd (even) numbers of elementary fermions. The electron (hole)-type c-particles carry negative (positive) charge. Electron (hole)-type Cooper-pair-like c-bosons are generated by the phonon-exchange attraction from a pair of electron (hole)-type c-fermions. The pair operators B are defined by

(15)

The prime on the summation in Equation (12) means the restriction:

(16)

The pairing interaction terms in Equation (12) conserve the charge. The term, where is the

pairing strength, generates a transition in electron-type c-particle states. Similarly, the exchange of a phonon

generates a transition between hole-type c-particle states, represented by. The phonon exchange

can also pair-create (pair-annihilate) electron (hole)-type c-boson pairs, and the effects of these processes are

represented by .

The Cooper pair, also called the pairon, is formed from two “electrons” (or “holes”). The pairons move as bosons, which are shown in Appendix. Likewise the c-bosons may be formed by the phonon-exchange attraction from two like-charge c-fermions. If the density of the c-bosons is high enough, then the c-bosons will be Bose- condensed and exhibit a superconductivity.

The pairing interaction terms in Equation (12) are formally identical with those in the generalized BCS Hamiltonian [13] . Only we deal here with c-fermions instead of conduction electrons.

The c-bosons, having the linear dispersion relation, can move in all directions in the plane with the constant speed [13] . For completeness we show the linear dispersion relation in Appendix. The supercurrent is generated by c-bosons monochromatically condensed, running along the sample length. The supercurrent density (magnitude) j, calculated by the rule:

(17)

is given by

(18)

where is the effective charge of carriers. The induced Hall field (magnitude) equals. The magnetic flux is quantized:

(19)

where is the fluxon number, and

(20)

Hence we obtain the Hall resistivity as

(21)

For the integer QHE at, we have,. Hence, we obtain, the plateau value observed.

The supercurrent generated by equal numbers of ± c-bosons condensed monochromatically is neutral. This is reflected in our calculations in Equation (18). The supercondensate whose motion generates a supercurrent must be neutral. If it has a charge, it would then be accelerated indefinitely by any external electric field because the impurities and phonons cannot stop the supercurrent to grow. That is, the circuit containing a superconducting sample and a battery must be burnt out if the supercondensate is not neutral. In the calculation of in

Equation (21), we used the unaveraged drift velocity, which is significant. Only the un-

averaged drift velocity cancels out exactly from numerator/denominator, leading to an exceedingly accurate plateau value.

We now extend our theory to include elementary fermions (electron, fluxon) as members of the c-fermion set. We can then treat the 2D superconductivity and the QHE in a unified manner. The c-boson containing one electron and one fluxon can be used to describe the principal QHE. Important pairings and effects are listed below: a) a pair of conduction electrons, superconductivity; b) c-fermions and fluxon, QHE; c) a pair of like- charge conduction electrons with two fluxons, QHE in graphene.

5. Superconductivity in C₈K, CaC₆ and MgB₂

5.1. Preliminaries

5.1.1. “Electrons”, “Holes” and “Phonons”

The conduction electrons (“electrons”, “holes”) are excited based on the orthogonal unit cells. As mentioned earlier the “electrons” are the majority carriers in both graphene and graphite. The excitation energy for the “electrons” is smaller than for the “holes”. Phonons are generated based on the same orthogonal unit cells. Phonons are bosons, and hence can be generated with no activation energies. The phonons are distributed, following the Planck distribution function:

(22)

which is a sole function of the Kelvin temperature T.

As an example consider acoustic phonons with a linear dispersion relation:

(23)

where s is the sound speed. The phonon size may be characterized by the average wave length:

(24)

The average size of phonons at the room temperature is greater by a few orders of magnitudes than the electron size.

5.1.2. The Ground-State Cooper Pair (Pairon) Energy

Cooper solved the Cooper equation [Ref. 12, Equation (1)] with a negative interaction energy constant, , and obtained the ground-state pairon energy:

(25)

where = Deby frequency, = density of states at the Fermi energy. The energy is singular at. Hence, this bound-state energy cannot be obtained by a perturbation theory. For illustration, consider a hydrogen atom levels problem with a negative Coulomb interaction. The bound states and energies are obtained by directly solving the Schrödinger equation with the full Hamiltonian containing the kinetic energy and the interaction energy. The Cooper pair is formed from two “electrons” (or “holes”). Likewise the c-bosons may be formed by the phonon-exchange attraction from c-fermions and fluxons. If the density of the c-bosons is high enough, then the c-bosons will be Bose-condensed and exhibit a supercon- ductivity.

5.2. The Superconductivity in GIC and MgB₂

The superconductivity occurs only in regular crystals. That is, it occurs only in crystals and not in liquids. C₈K and graphene have a 120˚ rotation symmetry. C₆Ca has a base-hexagonal (60˚ rotation) symmetry.

C₈K has graphene sheets, and each sheet is likely to become superconducting below the critical temperatures. The numbers of “electrons” and “holes” depend on the environments arising from the lattice structures. Since the lattice structures are very different in C₈K and C₆Ca, the critical temperatures should be different significantly.

BCS [5] used the fermionic pair operator equation.

(26)

constructed a ground-state vector and obtained a ground-state energy of an electron-phonon system:

(27)

where N is the pairon number per spin and the ground-state energy of the pairon, see Equation (17). The center-of-mass (CM) of the pairons move as bosons. That is, the eigenvalues of the pairon number operator are unlimited:

(28)

which is shown below.

The number operator in the k-q representation

(29)

has eigenvalues 0 or 1: [13]

(30)

The total number of a system of pairons, N, is represented by

(31)

where

(32)

represents the number of pairons having net momentum. From Equations (30)-(32) we can establish Equation (28). To explicitly see this property, we introduce

(33)

and obtain, after simple calculations,

(34)

Although the occupation number is not connected with as, the eigenvalues of satisfying Equation (34) can be shown straightforwardly to yield Equation (28) with the eigenstates, , ,.

The present author’s group [7] [8] [13] regards the superconductivity as a result of the BEC of the c-bosons. The free c-bosons moving in 2D with the linear dispersion relation undergoes a BEC at [13]

(35)

where is the pairon number density. The derivation of the linear dispersion relation and the BEC is outlined in Appendix. The average interpairon distance

(36)

is greater several times than the BCS coherence length (pairon size):

(37)

where is the zero temperature BCS energy gap. We have

(38)

Thus 2D pairons do not overlap in space. Hence the can be calculated based on the free moving pairons model. See Ref. 12 for more details.

Formula (25) is distinct from the BCS formula in the weak coupling limit:

(39)

Our Formula (35) obtained after identifying superconducting temperature as the BEC condensation temperature contains familiar quantities, the Fermi speed and the boson density only.

For illustration let us take GaAs/AlGaAs. We assume and, then we obtain, (reasonable). Not all electrons are bound with fluxons since the simul- taneous generation of ± c-bosons is required. The plateau width vanishes at since the energy gap vanishes there.

The neutral supercondensate is generated from the two ranges of energies of “electrons” and “holes”. Hence it is difficult to precisely determine the critical temperature from the theoretical consideration alone. The com- parison between theory and experiment may be carried out as follows. First we find the Fermi speed from the Hall effect measurements or others. We then find the supercondensate density from the measurered critical temperature by using Equation (35). In the mean field approximation we obtain

(40)

which indicates a close connection between the zero temperature gap and the critical temperature. A rigorous treatment of the BEC of free pairons shows a phase transition of the third order [13] . The molar heat rises like, reaches 4.38 R (R = gas constant) at, and then decreases to 2R in the high-temperature limit [14] as shown in Figure 4. We note that the molar heat does not vanish above.

6. Summary and Discussion

We have developed a theory regarding MgB₂ as a member of GIC. We start with the lattice configuration with all ions locations specified, and find that each B-plane contains B’s forming a honeycomb lattice of the nearest neighbour distance (lattice constant) while each Mg-plane contains a base-hexagonal lattice of the lattice constant. Since the B-lattice is more compact, it becomes superconducting at the lowest temperatures.

We obtain a linear dispersion relation for the moving pairons. The superconducting temperature, identified as the BEC temperature of the pairons, is given by. The supercurrent density is

calculated without introducing the averaging. The superconducting energy gap is identified as the gap in the pairon energy spectrum, distinct from the BCS energy gap.

Canfield and Crabtree have discussed two energy gaps, which is strange since there is one superconducting state at 0 K. We shall discuss this topic in a separate publication.

Appendix: Linear Dispersion Relation and Bose-Einstein Condensation

We consider the case of a 2D superconductor. The phonon exchange attraction is in action for any pair of electrons near the Fermi surface. In general the bound pair has a net momentum, and hence, it moves. Such a pair is called a moving pairon. The energy of a moving pairon can be obtained from

(41)

which is Cooper’s equation in 2D, Equation (1) of his 1956 Physical Review paper [12] . The prime on the -integral means the restriction on the integration domain arising from the phonon exchange attraction, see below. The pair wavefunctions are coupled with respect to the other variable, meaning that the exact (energy-eigenstate) pair wavefunctions are superpositions of.

Equation (41) can be solved simply. We briefly review the calculations and results here. We assume that the energy is negative:

(42)

Then,. Rearranging the terms in Equation (41) and dividing by

, we obtain from Equation (41)

(43)

where

(44)

is k-independent. Introducing Equation (43) in Equation (44), and dropping the common factor, we obtain

(45)

We now assume a free-electron model in 2D. The Fermi surface is a circle of the radius (momentum)

(46)

where represents the effective mass. The energy is given by

(47)

The prime on the k-integral in Equation (45) means the restriction:

(48)

We may choose the z-axis along as shown in Figure 5.

The k-integral in Equation (45) can then be expressed by

(49)

where is

(50)

After performing the integration and taking the small-q and small- limits, we obtain

(51)

where

(52)

is the pairon ground state energy.

As expected, the zero-momentum pair has the lowest energy. The excitation energy is continuous with no energy gap. The energy increases linearly with momentum q for small q. Hence, the Cooper pair moves like a massless particle with a common speed.

Such a linear dispersion relation is valid for pairs moving in any dimensions (D). However the coefficients slightly depend on the dimension as follows:

(53)

where and for 3 and 2 D, respectively.

The velocity of the particle having a linear dispersion relation is defined and calculated as

(54)

The velocity magnitude is c. Hence, the pair moves with the speed c.

We consider a system of free bosons having a linear dispersion relation: moving in 2 D. The system undergoes a Bose-Einstein condensation with the critical temperature:

(55)

where n is the 2D boson density. The is proportional to the square root density. The derivation of Equation (55) is given in Ref. 13. Briefly, the chemical potential vanishes below and decreases further above. The difference between the boson density n and the zero momentum density is given by

(56)

where,. We put on the right-hand side and and on the left-hand side, and obtain Equation (55).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Nagamatsu, J., Nakagawa, N., Muranaka, T., Zenitani, Y. and Akimitsu, J. (2001) Nature, 410, 63. http://dx.doi.org/10.1038/35065039
[2]	Canfield, P.C. and Crabtree, G.W. (2003) Physics Today, 56, 34. http://dx.doi.org/10.1063/1.1570770
[3]	Hinks, D.G., Claus, H. and Jorgenson, J.D. (2001) Nature, 411, 457. http://dx.doi.org/10.1038/35078037 Kortus, J., et al. (2001) Physical Review Letters, 86, 4656. http://dx.doi.org/10.1103/PhysRevLett.86.4656
[4]	Uchida, S. (2015) High Temperature Superconductivity. Springer, Japan, 9.
[5]	Bardeen, J., Cooper, L.N. and Schrieffer, J.R. (1957) Physical Review, 108, 1175. http://dx.doi.org/10.1103/PhysRev.108.1175
[6]	Ashcroft, N.W. and Mermin, N.D. (1976) Solid State Physics. Saunders, Philadelphia, 6-7, 216-217, 228-229.
[7]	Fujita, S., Takato, Y. and Suzuki, A. (2011) Modern Physics Letters B, 25, 223. http://dx.doi.org/10.1142/S021794911025675
[8]	Fujita, S. and Suzuki, A. (2010) Journal of Applied Physics, 107, 013711. http://dx.doi.org/10.1063/1.3280035
[9]	Kang, N., Lu, L., Kong, W.J., Hu, J.S., Yi, W., Wang, Y.P., Zhang, D.L., Pan, Z.W. and Xie, S.S. (2003) Physical Review B, 67, 033404. http://dx.doi.org/10.1103/PhysRevB.67.033404
[10]	Zhang, S.C., Hansson, T.H. and Kivelson, S. (1989) Physical Review Letters, 62, 82. http://dx.doi.org/10.1103/PhysRevLett.62.82
[11]	Ehrenfest, P. and Oppenheimer, J.R. (1931) Physical Review, 37, 333. http://dx.doi.org/10.1103/PhysRev.37.333 Bethe, H.A. and Jackiw, R.W. (1989) Intermediate Quantum Mechanics. 2nd Edition, Benjamin, New York, 23. Fujita, S. and Morabito, D.L. (1998) Modern Physics Letters B, 12, 1061.
[12]	Cooper, L.N. (1956) Physical Review, 104, 1189. http://dx.doi.org/10.1103/PhysRev.104.1189
[13]	Fujita, S. and Godoy, S. (2001) Theory of High Temperature Superconductivity. Kluwer, Dordrecht, 54-58, 96-98, 107-109, 164-167, 230-231. http://dx.doi.org/10.1007/0-306-48216-9
[14]	Fujita, S., Ito, K. and Godoy, S. (2009) Quantum Theory of Conducting Matter—Superconductivity. Springer, New York, 79-83. http://dx.doi.org/10.1007/978-0-387-88211-6