Cecilia N. Okoli^1*, Sidney I. Onyeagu², George A. Osuji^2
1Department of Statistics, Anambra State University, Uli, Nigeria.
²Department of Statistics, Nnamdi Azikiwe University, Awka, Nigeria.
DOI: 10.4236/oalib.1101189   PDF    HTML   XML   1,174 Downloads   2,290 Views   Citations

Abstract

In this paper, we proposed the generalized method and algorithms developed for estimation of parameters and best model fits of log linear model for n-dimensional contingency table. For purpose of this work, the method was used to provide parameter estimates of log-linear model for three-dimensional contingency table. In estimating parameter estimates and best model fit, computer programs in R were developed for the implementation of the algorithms. The iterative proportional fitting procedure was used to find the parameter estimates and goodness of fits of the log linear model. Akaike information criteria (AIC) and Bayesian information criteria (BIC) were used to check the adequacy of the model of the best fit. Secondary data were used for illustration and the result obtained showed that the best model fit for three-dimensional contingency table had a generating class: [CA, AB]. This showed that the best model fit had sufficient evidence to fit the data without loss of information. This model also revealed that breed was independent of chick loss given age. The best model in harmony with the hierarchy principle is Logm_ijk＝μ_＋μ_C(i)＋ μ_A(j)＋ μ_B(k)＋ μ_CA(ij)＋ μ_AB(jk).

Keywords

Hierarchical Log Linear Models, Categorical Data, Contingency Table, Likelihood Ratio Test Statistic, AIC, BIC, Interaction

Share and Cite:

Keywords:

Subject Areas: Mathematical Analysis, Mathematical Statistics

1. Introduction

Contingency tables [1] are formed when a population is cross-classified according to a series of categories (or factors). Additionally, n-contingency table is a contingency table created by cross-classification of more than two categorical variables. A categorical variable is one for which the measurement scale consists of a set of categories. Categorical data are data consisting of counts of observation falling in different categories. Categorical data in contingency tables are collected in many investigations. In order to understand the type of structures in such data appropriate log linear models are fitted. Log linear models are used to model the observed cell count where the log of expected cell count is proportional to linear combination involving number of model parameters. Log-linear models are used to determine whether there are any significant relationships in n-way contingency tables that have three or more categorical variables and/or to determine if the distribution of the counts among the cells of a table can be explained by a simpler, underlying structure (restricted model). It is a specialized case of generalized linear model for Poisson distributed data and is more commonly used for analyzing n-dimensional contingency tables that involve more than two variables, though it can also be used to analyze two-way contingency table [2] . A saturated model imposes no constraints on the data and always reproduces the observed counts. The parsimonious model in log linear model analysis is an incomplete model that achieves satisfactory level of goodness of fit. The log linear model is called a hierarchical model; whenever a higher-order interactions is included, lower-order interactions composed of these variables must also be included. The reason for including lower-order terms is that the statistical significance and practical interpretation of higher-order terms depend on how the variables are coded. This is undesirable, but with hierarchical models, the same results are obtained, irrespective of how the variables are coded [1] . Akaike information criteria and Bayesian information criteria are used for checking adequacy of model fit. The comparison of the model using information criteria can be viewed as equivalent to likelihood ratio test and understanding the differences among criteria may make it easier to compare the results and use them to make informed decisions [3] . The aim of this research work is to use a generalized method for estimation of parameters and algorithms developed implemented in R computer programs for estimating the parameter estimates and best model fit of log linear model for three- dimensional contingency table.

2. Review of Related Literature

[4] presented a survey on the theory of multidimensional contingency tables and showed that estimation and performance of asymptotic as well as exact tests are simple if only the decomposable models are considered.

[5] emphasized on log linear analysis of cross classification tables with ordinal variables. He also compared chi square of independence with log linear model of independence. The result showed that the log linear model is more adequate for the test.

[6] applied log linear model on categorical data cross-tabulated on contingency table and the results was shown for the hypothesis testing and model building for the categorical data.

[7] applied hierarchical log linear analysis method to occupational fatalities in the underground coal mines of Turkish Hardcoal Enterprises. The accidents records were evaluated and the main factors affecting the accidents were defined. The results found showed that the mostly affected job group by the fatality accidents was the production workers and these workers were mostly exposed to roof collapses and methane explosions.

[8] presented a modeling effort in estimating the relationships between driver’s fault and carelessness and the traffic variables. The result of the analysis showed that the best fit model regarding these variables was log- linear model. Also, the associations of the factors with the accident severity and the contributions of the various factors and interactions between these variables were assessed. The obtained results provided valuable information in regard to preventing undesired consequences of traffic accidents.

[9] described the log linear model as a frame work for analyzing effects in contingency tables. That is, tables of frequencies formed by two or three variables of classification and he considered variables to have nominal categories. He further considered two test procedures via maximum likelihood estimation of expected cell frequencies and associated chi-square tests and chi-square tests based on logarithm of adjusted cell frequencies for testing for parameter of the model.

3. Methodology

3.1. Data Collection

Data for 510 chickens on breed, age and chick loss were collected from poultry record book of Sambo feeds, Awka, Nigeria. The breed, age, and chick loss were classified into two, three and two categories of levels respectively.

3.2. Proposed Generalized Method

For any 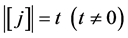and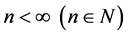, we define

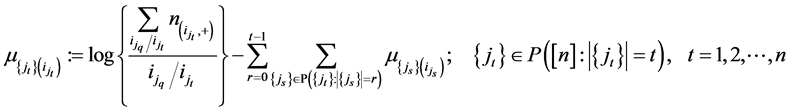
where, 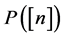is the power set of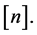

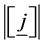is the level of interaction/cardinality of the set/length of element in the set. 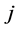is a member of collec-

tions of sequence 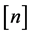and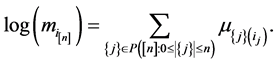

For the saturated log linear model for 3-diimensional contingency table and its parameters effects is given by

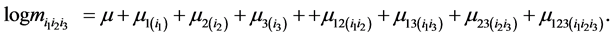(1)

Conventionally, we take 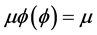and

;

;

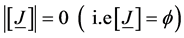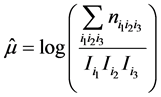
3.3. Iterative Proportional Fitting Procedure

The iterative proportional fitting (IPF) in [10] is used to estimate model parameters and best model fit of log linear model. This is to ensure that the expected values are obtained iteratively for model whose expected values are not directly obtainable from marginal totals of observed values. For example if we consider 3-dimensional table, for model of No-three factor interaction or pair-wise association, IPF algorithm for find-

ing expected frequencies.

The’s of the model is characterized by fitted margins, ,

The procedure assumes initial value, the modifications are

(3.01)

(3.02)

(3.03)

The second cycle is of the same form as the first cycle above but uses updated estimates

(3.04)

(3.05)

(3.06)

The steps are repeated until convergence to desired accuracy is attained.

3.4. Comparison of Models and Goodness of Fit Measure

The goodness of fit can be assessed by a number of statistics. The statistics include Pearson chi-square test statistic due to [11] ; likelihood ratio statistic due to [12] ; Modified log likelihood ratio due to [13] ; Neyman modified chi-square due to [14] ; Modified Freeman Tukey due to [15] . Comparative studies have suggested preference for Statistic over others due to decomposability into small components and simplicity when comparing two models [16] .

statistic is given as

(2)

where is chi-square distributed with degree of freedom (d.f) equal to:

d.f = number of cells in the table-number of independent parameters estimated.

3.5. Information Theory Measures of Model Fit

Information criteria should be considered also for testing the adequacy of the model fit. Akaike information criteria [3] are given as:

(3)

Another information criteria is Bayesian information [17] is given as

(4)

where and d.f is the total sample size and degree of freedom respectively.

4. Analysis and Results

Implementation of Algorithms in r for Estimating Parameter Estimates, Expected Values and Goodness of Fit of Log Linear Model for 3-Dimensional Contingency Table

> I=2; J= 3; K= 2

>n=c(55, 67, 16, 44, 8, 45, 48, 66, 20, 52, 18, 71)

> n=array(n, dim=c(I, J, K))

> dimnames(n)=list(Chicksloss=c("Yes", "No"), Age=c(1, 2, 3), Breed=c("Broiler", "Old layer"))

> n

, , Breed = Broiler

Age

Chicksloss 1 2 3

Yes 55 16 8

No 67 44 45

, , Breed = Old layer

Age

Chicksloss 1 2 3

Yes 48 20 18

No 66 52 71

> mu=log(sum(n)/(I*J*K))

> mu_1=mu_2=mu_3=0

> mu_12=matrix(0, I, J); mu_13=matrix(0, I, K); mu_23=matrix(0, J, K)

> for (i in 1:I){

+ mu_1[i]=log(sum(n[i, ,])/(J*K))-mu

+ for (j in 1:J){

+ mu_2[j]=log(sum(n[,j,])/(I*K))-mu

+ for (k in 1:K){

+ mu_3[k]=log(sum(n[, , k])/(I*J))-mu

+ }

+ }

+ }

> for (j in 1:J){

+ for (k in 1:K){

+ mu_13[i, k]=log(sum(n[i, , k])/J)-mu-mu_1[i]-mu_3[k]

+ }

+ }

> for (i in 1:I){

+ for (j in 1:J){

+ mu_12[i, j]=log(sum(n[i, j, ])/K)-mu-mu_1[i]-mu_2[j]

+ }

+ }

> for (j in 1:J){

+ for (k in 1:K){

+ mu_23[j, k]=log(sum(n[, j, k])/I)-mu-mu_2[j]-mu_3[k]

+ }

+ }

> mu; mu_1; mu_2; mu_3; mu_13; mu_12; mu_23

[1] 3.749504

[1] -0.4353181 0.3022809

[1] 0.3280334 -0.2529965 -0.1799714

[1] -0.08167803 0.07550755

[,1] [,2]

[1,] 0.0000000 0.00000000

[2,] -0.0188632 0.01584223

[,1] [,2] [,3]

[1,] 0.2993624 -0.17081773 -0.5692653

[2,] -0.1826164 0.07241258 0.1886294

[,1] [,2]

[1,] 0.11501445 -0.10999373

[2,] -0.01363215 0.01150382

[3,] -0.21070993 0.15044894

> m_1=m_2=m_3=m_4=array(0, dim=c(I, J, K))

> for(i in 1:I){

+ for (j in 1:J){

+ for (k in 1:K){

+ m_1[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k])

+ m_2[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_13[i, k])

+ m_3[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_12[i, k])

+ m_4[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_23[j, k])

+ }

+ }

+ }

> m_1; m_2; m_3; m_4

, , 1

[,1] [,2] [,3]

[1,] 35.18224 19.67820 21.16897

[2,] 73.56286 41.14533 44.26240

, , 2

[,1] [,2] [,3]

[1,] 41.1707 23.02768 24.77220

[2,] 86.0842 48.14879 51.79642

, , 1

[,1] [,2] [,3]

[1,] 35.18224 19.67820 21.16897

[2,] 72.18824 40.37647 43.43529

, , 2

[,1] [,2] [,3]

[1,] 41.17070 23.02768 24.77220

[2,] 87.45882 48.91765 52.62353

, , 1

[,1] [,2] [,3]

[1,] 47.46078 26.54586 28.55691

[2,] 61.28431 34.27767 36.87446

, , 2

[,1] [,2] [,3]

[1,] 34.70588 19.41176 20.88235

[2,] 92.54902 51.76471 55.68627

, , 1

[,1] [,2] [,3]

[1,] 39.47059 19.41176 17.14706

[2,] 82.52941 40.58824 35.85294

, , 2

[,1] [,2] [,3]

[1,] 36.88235 23.29412 28.79412

[2,] 77.11765 48.70588 60.20588

> model1=loglm(~Chicksloss + Age + Breed, data=n)

> model2=loglm(~Chicksloss + Age+ Breed + Chicksloss*Breed, data=n)

> model3=loglm(~Chicksloss + Age+ Breed + Chicksloss*Age, data=n)

> model4=loglm(~Chicksloss + Age+ Breed + Age*Breed, data=n)

> model1; model2; model3; model4

Call:

loglm(formula = ~Chicksloss + Age + Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 37.13769 7 4.41719e-06

Pearson 36.33465 7 6.26767e-06

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Breed,

data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 36.81976 6 1.909229e-06

Pearson 35.20502 6 3.932731e-06

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Age,

data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 8.280408 5 0.1414439

Pearson 8.181170 5 0.1465296

Call:

loglm(formula = ~Chicksloss + Age + Breed + Age * Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 29.68738 5 1.699225e-05

Pearson 28.75595 5 2.588877e-05

> m_5a=m_5b=m_5c=m_6=array(0, dim=c(I, J, K))

> for(i in 1:I){

+ for (j in 1:J){

+ for (k in 1:K){

+ m_5a[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_12[i, j]+mu_13[i,k])

+ m_5b[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_12[i, j]+mu_23[j,k])

+ m_5c[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_13[i, k]+mu_23[j,k])

+ m_6[i, j, k]=exp(mu+mu_1[i]+mu_2[j]+mu_3[k]+mu_12[i, j]+mu_13[i,k]+mu_23[j, k])

+ }

+ }

+ }

> m_5a; m_5b; m_5c; m_6

, , 1

[,1] [,2] [,3]

[1,] 47.46078 16.58824 11.98039

[2,] 60.13913 43.40870 52.45217

, , 2

[,1] [,2] [,3]

[1,] 55.53922 19.41176 14.01961

[2,] 72.86087 52.59130 63.54783

, , 1

[,1] [,2] [,3]

[1,] 53.24576 16.36364 9.704225

[2,] 68.75424 43.63636 43.295775

, , 2

[,1] [,2] [,3]

[1,] 49.75424 19.63636 16.29577

[2,] 64.24576 52.36364 72.70423

, , 1

[,1] [,2] [,3]

[1,] 39.47059 19.41176 17.14706

[2,] 80.98723 39.82979 35.18298

, , 2

[,1] [,2] [,3]

[1,] 36.88235 23.29412 28.79412

[2,] 78.34909 49.48364 61.16727

, , 1

[,1] [,2] [,3]

[1,] 53.24576 16.36364 9.704225

[2,] 67.46947 42.82096 42.486732

, , 2

[,1] [,2] [,3]

[1,] 49.75424 19.63636 16.29577

[2,] 65.27166 53.19980 73.86519

> model5a=loglm(~Chicksloss + Age+ Breed + Chicksloss*Age + Chicksloss *Breed, data=n)

> model5b=loglm(~Chicksloss + Age+ Breed + Chicksloss*Age + Age*Breed, data=n)

> model5c=loglm(~Chicksloss + Age+ Breed + Chicksloss* Breed + Age*Breed, data=n)

> model6=loglm(~Chicksloss + Age+ Breed + Chicksloss*Age + Chicksloss *Breed + Age*Breed , data=n)

>model5a; model5b; model5c; model6

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Age +

Chicksloss * Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 7.962476 4 0.09296247

Pearson 7.853555 4 0.09709239

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Age +

Age * Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 0.8301007 3 0.8422546

Pearson 0.8172251 3 0.8453427

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Breed +

Age * Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 29.36945 4 6.576301e-06

Pearson 28.32066 4 1.073878e-05

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Age +

Chicksloss * Breed + Age * Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 0.8263105 2 0.6615596

Pearson 0.8145226 2 0.6654703

> model7=loglm(~Chicksloss + Age+ Breed + Chicksloss*Age *Breed, data=n); model7

Call:

loglm(formula = ~Chicksloss + Age + Breed + Chicksloss * Age *

Breed, data = n)

Statistics:

X^2 df P(> X^2)

Likelihood Ratio 0 0 1

Pearson 0 0 1

5. Discussion

The best model fit that explained the observed data is [CA, AB]. This model means that at significance level of 5%, the data provide sufficient evidence (likelihood ratio = 0.83, d.f = 2, P = 0.84 or Pearson 0.82, d.f = 2, P = 0.84) that breed and chickloss are independent given the Age, thus the association or relationship between the breed and chickloss is independent for each age (Table 1).

The results of AIC and BIC confirmed that best model (CA, AB) adequately fit the data (Table 2).

6. Conclusions

A generalized method and algorithms developed for estimation of the parameters and best model fits of log linear model for n-dimensional contingency table. Three-dimensional contingency table was considered for this paper. In estimating these parameter estimates and best model fits, computer programs in R were developed for the implementation of the algorithms. The iterative proportional fitting procedure was used to estimate the parameter estimates and goodness of fits of the log linear model.

The results of the analysis showed that the best model fit for 3-dimensional contingency table was. This shows that the best model fit has sufficient evidence to fit the data without loss of information. This model also revealed that breed was independent of chick loss given age. It also discovered that the results of the goodness of fit showed that the best model adequately fit the data having the highest P-value and least likelihood ratio

P-value for.

estimate. The values of the best of fit statistics are: likelihood ratio, d.f = 3, and P-value = 0.84; Pearson chi-square, d.f = 3, and P-value = 0.84. The results of AIC and BIC confirmed the best

model adequacy to the data. The final model in harmony with the hierarchy principle is written as:

NOTES

^*Corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Agresti, A. (2002) Categorical Data Analysis. 2nd Edition, John Wiley & Sons, Inc., New York, 320-332. http://dx.doi.org/10.1002/0471249688
[2]	Knoke, D. and Burke, P.J. (1980) Log-Linear Models. Sage Publications, Inc., New Jersey, 8-17.
[3]	Akaike, H. (1987) Factor Analysis and AIC. Psychometrika, 52, 317-332. http://dx.doi.org/10.1007/BF02294359
[4]	Anderson, A.H. (1974) Multidimensional Contingency Tables. Scandinavean Journal of Statistics, 1, 115-127.
[5]	Green, J.A. (1988) Bayesian Model Comparison for the Order Restricted RC Association Model. Psychometrica, 74, 561-587.
[6]	Marascuilo, L. (1987) Log Linear Models: A Way to Study Main Effects and Interactions for Multidimensional with Categorical Data. Journal of America Psychological Associations, 34, 443-445.
[7]	Onder, M. and Adiguzel, E. (2010) Evaluation of Occupational Facilities among Underground Coal Mine Workers through Log-Linear Models. Industrial Health, 48, 872-878. http://dx.doi.org/10.2486/indhealth.MS1136
[8]	Olmus, H. (2012) Analysis of Traffic Accidents Caused by Drivers Using Log-Linear Models. Promet—Traffic & Transportation, 24, 495-504.
[9]	Shaffer, J.P. (1973) Defining and Testing Hypothesis in Three-Dimensional Contingency Tables. Psychological Bulletin, 79, 127-141. http://dx.doi.org/10.1037/h0033865
[10]	Deming, W.E. and Stephen, F.F. (1940) On Least Square Adjustment of a Frequency Tables When the Expected Marginal Totals Are Known. Annals of Mathematical Statistics, 11, 427-444. http://dx.doi.org/10.1214/aoms/1177731829
[11]	Pearson, K. (1990) On a Criterion That a Given System of Derivations from Probable in the Case of a Corrected System of Variables Is Such That It Can Be Reasonably Supposed to Have Arisen from a Random Sampling. Philosophical Magazine, 50, 157-175. http://dx.doi.org/10.1080/14786440009463897
[12]	Wilks, S.S. (1938) The Large Distribution of the Likelihood Ratio for Testing Composite Hypotheses. Annals of Mathematical Statistics, 9, 60-62. http://dx.doi.org/10.1214/aoms/1177732360
[13]	Kullback, S. (1959) Information Theory and Statistics. Wiley, New York.
[14]	Neyman, J. (1949) Contribution to the Theory of Chi-Square Test. Proceedings of the First Berkeley Symposium on Mathematical Statistics and Probability, 239-273.
[15]	Bishop, Y.M.M., et al. (1975) Discrete Multivariate Analysis: Theory and Practice. Mass MIT Press, Cambridge, 18-37.
[16]	Lawal, H.B. (2003) Categorical Data Analysis with SAS and SPSS Applications. Lawrence Erlbaum Associates, Inc., New Jersey, 83-128.
[17]	Raftery, A.E. (1986) A Note on Bayesian Factors for Log-Linear Contingency Table Models with Vague Prior Information. Journal of the Royal Statistical Society, Series B, 48, 249-250.