Received 6 May 2016; accepted 1 July 2016; published 4 July 2016
1. Introduction
Population competition systems of Lotka-Volterra type have been investigated extensively in recent years [1] - [5] . The basic and the simplest two species nonautonomous competitive system for Lotka-Volterra type is as following form
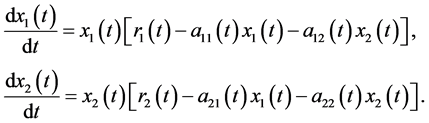(1)
There is an extensive literature concerned with the properties of system (1) that has been discussed by many authors [1] - [4] .
However, in the real world, the growth rate of a natural species will not often respond immediately to changes in its own population or that of an interacting species, but will rather do so after a time lag [6] . Recently, many people are doing research on the dynamics of population with time delays, which is useful for the control of the population of mankind, animals and the environment. Therefore, it is essential for us to investigate population systems with time delays. In this paper, we investigate the following two species Lotka-Volterra type competitive systems with pure discrete time delays
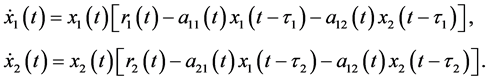(2)
By using the technique of comparison method and Liapunov function method, we will establish some sufficient conditions on the boundedness, permanence, existence of positive periodic solution and global attractivity of the system.
The organization of this paper is as follows. In the next Section, we will present some basic assumptions and main definition and lemmas. In Section 3, conditions for the positivity and boundedness are considered. In the final Section, we considered the conditions for the permanence, existence of positive periodic solution and global attractivity of the system.
2. Preliminaries
In system (2), we have that 
represent the density of two competitive species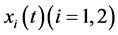 
at time t, respectively; 
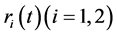represent the intrinsic growth rate of species 
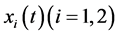at time t, respectively; 
and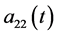 
represent the intra patch restriction density of species 
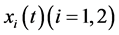at time t, respectively; 
and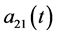 
represent the competitive coefficients between two species 
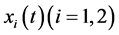at time t, respectively. 
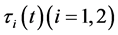represent the time delay in the model. In this paper, we always assume that
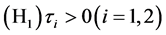are positive constants, 
, ![]()
are continuous positive functions.
![]()
are positive constants, ![]()
, ![]()
are continuous positive ω-peri- odic functions.
From the viewpoint of mathematical biology, in this paper for system (2) we only consider the solution with the following initial conditions
![]()
(3)
where ![]()
are nonnegative continuous functions defined on ![]()
satisfying ![]()
with![]()
.
In this paper, for any continuous function ![]()
we denote
![]()
Now, we present some useful definitions.
Definition 1. (see [7] ) System (2) is said to be permanent if there exists a compact region ![]()
such that every solution ![]()
of system (2) with initial conditions (3) eventually enters and remains in the region D.
Definition 2. (see [8] ) System (2) is said to be global attractive, if for any two positive solutions
![]()
and ![]()
of system (2), one has
![]()
The following two lemmas will be used in the proof of the main results of system (2).
Lemma 1. (see [9] ) Consider the following equation:
![]()
where, ![]()
, we have
1) If![]()
, then![]()
.
2) If![]()
, then![]()
.
Lemma 2. (see [10] ) Let ![]()
be a nonnegative function defined on![]()
, such that ![]()
is integrable on ![]()
and uniformly continuous on![]()
. Then,![]()
.
3. Positivity and Boundedness
In this section, we will obtain positivity and boundedness of system (2). The following Lemma is about the positivity of system (2).
Lemma 1. Set ![]()
is positively invariant for system (2).
The proof of Lemma1 is simple, and here we omit it.
The following theorem is about the boundedness of system (2).
Theorem 1. Suppose that assumption (H1) holds, then there exist positive constants ![]()
such that
![]()
for any positive solution ![]()
of system (2).
Proof: Let ![]()
be a solution of system (2). Firstly, it follows from the first equation of system (2) that for![]()
, we have
![]()
We consider the following auxiliary equation
![]()
By Lemma 2, we derive
![]()
By comparison, there exists a ![]()
such that ![]()
for![]()
.
Next, by using an argument similar in the above, there exist a ![]()
such that![]()
, where
![]()
This completes the proof.
The following theorem is about the global attractivity of system (2). Firstly, for convenience we denote the following functions
![]()
where,
![]()
(4)
where, ![]()
and ![]()
are constants.
4. Permanence, Existence of Positive Periodic Solution and Global Attractivity
In this section, we will obtain the permanence, existence of positive periodic solution and global attractivity of system (2). First we obtain the global attractivity of system (2).
Theorem 2. Suppose that (H1) and there exists a constant ![]()
such that
![]()
Then system (2) has a positive solution which is globally attractive.
Proof: Let ![]()
and ![]()
are any two positive solutions of system (2). From Theorem 1, choose positive constants ![]()
such that
![]()
(5)
for all![]()
. Let
![]()
Calculating the upper right derivation of ![]()
along system (2) for all![]()
, we have
![]()
(6)
Define
![]()
where
![]()
Calculating the upper right derivative of ![]()
and from (6), we have
![]()
(7)
Define
![]()
where
![]()
Further, we define a Liapunov function as follows
![]()
Calculating the upper right derivation of![]()
, from (6) and (7) we finally can obtain for all ![]()
![]()
(8)
From assumption (H2), there exists a constant ![]()
and ![]()
such that for all ![]()
we have
![]()
(9)
Integrating from ![]()
to t on both sides of (8) and by (9) produces
![]()
(10)
hence, ![]()
bounded on ![]()
and we have
![]()
(11)
From the boundedness of ![]()
and (11), we can obtain that ![]()
and their derivatives remain bounded on![]()
. Therefore ![]()
is uniformly continuous on![]()
. By Barbalat’s theorem it follows that
![]()
Therefore,
![]()
This completes the proof of Theorem 2.
From the global attractivity of system (2), we have the following result.
Corollary 1. Suppose that the conditions of Theorem 2 hold, then system (2) is permanent.
As a direct corollary of [11] (Theorem 2), from Corollary 1, we have the following result.
Corollary 2. Suppose that the conditions of Theorem 2 and (![]()
) hold, then system (2) has a positive ω-peri- odic solution which is globally attractive.
Acknowledgements
This work was supported by the Natural Science Foundation of Xinjiang University (Starting Fund for Doctors, Grant No. BS130102, BS150202) and the National Natural Science Foundation of China (Grant No. 11401509, 11261056).
NOTES
![]()
*Corresponding author.