Abstract

In this paper, to find the fixed points of the nonexpansive nonself-mappings, we introduced two new viscosity approximation methods, and then we prove the iterative sequences defined by above viscosity approximation methods which converge strongly to the fixed points of nonexpansive nonself-mappings. The results presented in this paper extend and improve the results of Song-Chen [1] and Song-Li [2].

Keywords

Fixed Points, Nonexpansive Nonself-Mappings, Viscosity Approximation Methods, Real Banach Space

Share and Cite:

Received 30 April 2016; accepted 27 June 2016; published 30 June 2016

1. Introduction

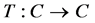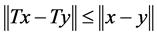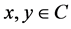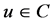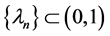Let C be a closed convex subset of a Hilbert space H and a nonexpansive mapping (i.e., for any). Let be a fixed point of T. Then for any initial and real sequence, we define a sequence 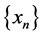by

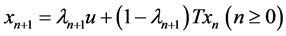(1)

Helpern [3] was the first to study the strong convergence of the iteration process (1). In 1992, Albert [4] studied the convergence of the Ishikawa iteration process in Banach space, which was extended the results of Mann iteration process [5] . But the mappings in these results must be self-mapping and continuous. It is more useful to get some results for nonself-mappings.

In 2006, Yisheng Song and Rudong Chen [1] studied viscosity approximation methods for nonexpansive nonself-mappings by the following iterative sequence.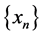

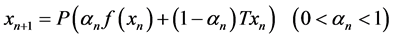
where X is a real reflexive Banach space, and C is a closed subset of X which is also a sunny nonexpansive retract of X. 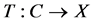is a nonexpansive mapping, 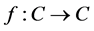is a fixed contractive mapping and P is a sunny nonexpansive retraction of X onto C.

In 2007, Yisheng Song and Qingchun Li [2] found a new viscosity approximation method for nonexpansive nonself-mappings as follows

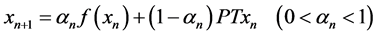
where X is a real reflexive Banach space, and C is a closed subset of X which is also a sunny nonexpansive retract of X. is a nonexpansive mapping, is a fixed contractive mapping and P is a sunny nonexpansive retraction of X onto C.

In this paper, we will study two new viscosity approximation methods for nonexpansive nonself-mappings in reflexive Banach space X, which can extend the results of Song-Chen [1] and Song-Li [2] on the two- dimensional space.

Let us start by making some basic definitions.

2. Preliminary Notes

Let X be a real Banach space with the norm, and be its dual space. When is a sequence in X, the

(respectively,) will denote the strong (respectively the weak, the weak star) convergence of the sequence to x.

Definition 2.1. Let X be a real Banach space and J denote the normalized duality mapping from X into given by

for all,

where denotes the dual space of X and denotes the generalized duality pairing.

Let denotes set of the fixed point of T.

Definition 2.2. Let X ba a real Banach space and T a mapping with domain and range in T. T is called nonexpansive if for any, such that (respectively T is called contractive if for any, such that), where.

Definition 2.3. Let X be a Banach space, C and D be nonempty subsets of X,. A mapping is called a retraction from C to D, if P is continuous with. A mapping is called a sunny, if, for all, , whenever. And a subset D of C is said to be a sunny nonexpansive retract of C, if there exists a sunny nonexpansive retraction of C onto D.

Definition 2.4. Let X be a real reflexive Banach space, which admits a weakly sequentially continuous duality mapping from X to, and C be a closed convex subset of X, which is also a sunny nonexpansive retract of X, and be nonexpansive mapping satisfying the weakly inward condition and, and is called contractive mapping. For a given and, let us define and by the following iterative scheme:

(2)

where, ,.

(3)

where, ,.

We call (2) the first type viscosity approximation method for nonexpansive nonself-mapping and call (3) the second type viscosity approximation method for nonexpansive nonself-mapping.

Let us introduce some lemmas, which play important roles in our results.

Lemma 2.1. ( [6] ) Let X be a real Banachspace, then for each, the following inequality holds:

, for

Lemma 2.2. ( [7] ) Let be three nonnegative real sequences satisfying

with,.

Then as

Lemma 2.3. ( [1] ) Let X be a real smooth Banach space, and C be nonempty closed convex subset of X, which is also a sunny nonexpansive retract of X and be mapping satisfying the weakly inward condition, and P be a sunny nonexpansive retraction of X onto C, then.

Lemma 2.4. ( [1] ) Let C be nonempty closed convex subset of a reflexive Banach space X which satisfies Opial’s condition, and suppose is nonexpansive. Then the mapping I-T is demiclosed at zero, i.e., , implies.

3. Main Results

First of all, let us study the first type viscosity approximation for nonexpansive nonself-mappings.

Lemma 3.1. ( [1] ) Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. Let be the unique fixed point of T, that is,

, for any,

where P is a sunny nonexpansive retract of X onto C. Then as, converges strongly to some fixed point p of T. And p is the unique solution in to the following variational inequality

For all.

Lemma 3.2. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X, which is also a sunny nonexpansive retract of X and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is a sequence by definition 2.4 (2), then the sequence is bounded.

Proof. Let, so we have

while,

therefore,

since

therefore, then is bounded.

Lemma 3.3. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is a sequence by definition 2.4 (2). Let us assume that there are two sequences, in satisfying the following conditions:

then

1)

2)

Proof by lemma 3.2, we know that the sequence is bounded. So the sequences, , are also bounded. Therefore, we have

(4)

by (4), we have

Set

Set, , ,

by the lemma 2.2 we have

Now we will proof as.

(5)

as, therefore

. (6)

Remark 3.1. From the lemma 3.1 we know that p is the unique solution in to the following variational inequality:

for all. (7)

Now, we can take a subsequence of such that

we may assume that by X is reflexive and is bounded. It follows from Lemma 2.3, Lemma 2.4, and (3.3), we have, by (7) we have

Theorem 3.4. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is the sequence by definition 2.4 (2). Let us assume there are two sequences, in satisfying the following conditions:

then the sequence converges strongly to the unique solution p of the variational inequality:

and for all.

Proof. Since C is closed, by lemma 3.2, is bounded, so, , are also bounded. Let be the sequence defined by

by the lemma 3.1 as we have converges strongly to a fixed point p of T and p is also the unique solution in to the following variational inequality

for all

using the remark 3.1, we have

By the definition 2.4 (2), we have

While

therefore,

where

Setting, , , and applying Lemma

2.1, we conclude that.

Let us prove p is the unique fixed point of T.

We assume that is another solution of (7) in, then and, so we have, which implies the equality.

Remark 3.2. when for all. The first type viscosity approximation methods for nonexpansive nonself-mappings (see definition 2.4) become the following iteration sequence:

.

So the theorem 3.4 improves the theorem 2.4 of Song-Chen [1] .

Now let us study the second type viscosity approximation for nonexpansive nonself-mappings.

Lemma 3.5. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X, which is also a sunny nonexpansive retract of X and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is a sequence by definition 2.4 (3), then the sequence is bounded.

Proof. Let, so we have

while,

therefore,

since

therefore, then is bounded.

Lemma 3.6. ( [2] ) Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. Let be the unique fixed point of T, that is,

, for any,

where P is a sunny nonexpansive retract of X onto C. Then as, converges strongly to some fixed point p of T. And p is the unique solution in to the following variational inequality:

for all.

Lemma 3.7. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is a sequence by definition 2.4 (3). Let us assume that there are two sequences, in satisfying the following conditions:

then

1)

2)

Proof by lemma 3.5, we know that the sequence is bounded. So the sequences, , are also bounded. Therefore, we have:

(8)

by (8), we have

Set

Set, , ,

by the lemma 2.2 we have

Now we will proof as.

(9)

as, , therefore

. (10)

Remark 3.3. From the lemma 3.6 we know that p is the unique solution in to the following variational inequality:

for all. (11)

Now, we can take a subsequence of such that

we may assume that by X is reflexive and is bounded. It follows from Lemma 2.3, Lemma 2.4, and (10), we have, by (11) we have

Theorem 3.8. Let X be a reflexive Banach space which admits a weakly sequentially continuous duality mapping J from X to X^*. Suppose C is a nonexpansive retract of X which is also a sunny nonexpansive retract of X, and is a nonexpansive mapping satisfying the weakly inward condition and, let be a fixed contractive mapping from C to C. And is the sequence by definition 2.4 (3). Let us assume there are two sequences, in satisfying the following conditions:

then the sequence converges strongly to the unique solution p of the variational inequality:

and for all.

Proof. Since C is closed, by lemma 3.5, is bounded, so, , are also bounded. Let be the sequence defined by

by the lemma 3.6 as we have converges strongly to a fixed point p of T and p is also the unique solution in to the following variational inequality

for all

using the remark 3.3, we have

By the definition 2.4 (3), we have

While

therefore,

where

Setting, , , and applying Lemma 2.1, we conclude that.

Let us prove p is the unique fixed point of T.

We assume that is another solution of (12) in, then and, so we have, which implies the equality.

Remark 3.4. When for all. The second type viscosity approximation methods for nonexpansive nonself-mappings (see definition 2.4) become the following iteration sequence:

.

So the theorem 3.8 improves the theorem 4.3 theorem 4.4 of Song-Li [2] .

4. Conclusion

In this paper, we studied two new viscosity approximation methods for nonexpansive nonself-mappings, which were defined by definition 2.4. And then we proved that the sequences which were defined by definition 2.4 converged strongly to the fixed point of T, which were the nonexpansive nonself mappings in Banach space.

Conflicts of Interest

The authors declare no conflicts of interest.

References