Abstract

We study projections onto a subspace and reflections with respect to a subspace in an arbitrary vector space with an inner product. We give necessary and sufficient conditions for two such transformations to commute. We then generalize the result to affine subspaces and transformations.

Keywords

Projection, Reflection, Commute, Inner Product, Affine Subspace

Share and Cite:

Received 4 April 2016; accepted 16 May 2016; published 19 May 2016

1. Introduction

Two lines and in 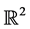are considered. When is the reflection over 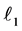followed by the reflection over 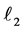the same as the reflection over 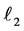followed by the reflection over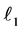? It is easy to see that it is the case if and only if 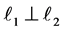or.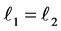

When considering subspaces of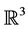, we can ask similar questions for lines, for planes or for the mixed case of one line and one plane. Instead of addressing those cases one by one, we generalize the situation of arbitrary two linear subspaces of a vector space with an inner product.

2. Projection

Supposing that U is a vector space equipped with an inner product, 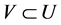is a linear subspace of U. Given a vector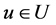, we know from linear algebra [1] [2] that u can be decomposed uniquely as 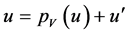where 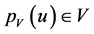is the projection of the vector u onto V and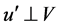, i.e..

Here are some elementary properties of the projection:

1) is linear.

2) if and only if.

3) if and only if

4).

5) If V₁ and V₂ are subspaces of U, then, for all.

6) If V₁, V₂ and W are subspaces of U, then.

7) If V₁, V₂ and W are subspaces of U, then.

Lemma 2.1. Supposing that U is a linear space and V, W are two linear subspaces of U, if then.

Proof. We first show that. Since and, we have. On the other hand, if, then, hence and thus. As a result,. The proof of is similar. +

Suppose U is a vector space and V, W are two subspaces of U. Intersecting the identity with V and W, we get and. It is obvious that these two sums are orthogonal.

Denote and. Using these notations, and.

Lemma 2.2. if and only if.

Poorf.

(Þ) If, then. On the other hand, by the fourth property of projection above,. Similarly,. Thus,.

(Ü) By Lemma 2.1,. For,

and, but, we must have, i.e.. Similarly,. +

Theorem 2.3. Supposing that U is a vector space and V, W are two subspaces of U, then if and only if.

Proof. (Þ) Assume that. In particular,

Thus,. Similarly,.

(Ü) Assume. By Lemma 2.2,.

Similarly,. +

3. Reflection over a Subspace

Supposing that U is a vector space equipped with an inner product, is a subspace of U. We define the refection of with respect to V as

The above formula can be easily derived from the observation that. Note that if,

then.

Lemma 3.1. Supposing that U is a vector space and V, W are two vector subspaces of U, then if and only if.

Proof.

Similarly,. Hence,

Theorem 3.2. Supposing that U is a vector space and V, W are two subspaces of U, then if and only if.

Poor. By Lemma 3.1, if and only if. By Theorem 2.3, if and only if. +

4. Projection onto a Translated Subspace

Define the projection of onto a translated subspace as

is well defined: supposing, then. Hence and thus

Theorem 4.1. if and only if and.

Proof.

Similarly,.

Thus, if and only if

(Þ) By Theorem 2.3, the first equation implies. The second equation simply means that.

(Ü) By Theorem 2.3, the first equation is satisifed. To show the second equation, since, we have, for some and, or:

which is the second equation.

5. Reflection over a Translated Subspace

We next discuss the reflection over a translated subspace. Let be a subspace. A translated subspace is for some. We define the reflection of over as

is well-defined: supposing, then and hence. As a result,

Supposing for some is another translated subspace.

Similarly,.

Theorem 5.1. if and only if and.

Proof. if and only if

(Þ) By Theorem 3.2, implies. The second equation simply means.

(Ü) We express and in terms of projections:

By Theorem 3.2, implies. By Lemma 3.1, we also have. To show, it suffices to verify the second equation

Since, we must have for some and, or:

6. Mixed Transformations

Theorem 6.1. if and only if and.

Theorem 6.2. if and only if and.

Theorem 6.3. if and only if and.

7. Generalizations

If we denote, the permutation group of order n, then

Theorem 7.1.

if and only if

Theorem 7.2.

if and only if

Theorem 7.3.

if and only if and

Theorem 7.4.

if and only if and

Conflicts of Interest

The authors declare no conflicts of interest.

References