Abstract

This article is a contribution to the study of the automorphism groups of  designs. Let be a non-trivial  design where for some positive integer , and  is block-transitive. If the socle of G is isomorphic to the simple groups of lie type, then G is not flag-transitive.

Keywords

Flag-Transitive, Block-Transitive, t-Design, Ree Group

Share and Cite:

Received 27 February 2016; accepted 4 April 2016; published 7 April 2016

1. Introduction

For positive integers 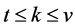and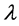, we define a 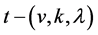design to be a finite incidence structure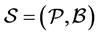, where denotes a set of points, , and a set of blocks, , with the properties that each block is incident with k points, and each t-subset of is incident with blocks. A flag of is an incident point-block pair with x is incident with B, where. We consider automorphisms of as pairs of permutations on and which preserve incidence structure. We call a group of automorphisms of flag-transitive (respectively block-transitive, point t-transitive, point t-homogeneous) if G acts transitively on the flags (respectively transitively on the blocks, t-transitively on the points, t-homogeneously on the points) of. For short, is said to be, e.g., flag-transitive if admits a flag-transitive group of automorphisms.

For historical reasons, a design with is called a Steiner t-design (sometimes this is also known as a Steiner system). If holds, then we speak of a non-trivial Steiner t-designs.

Investigating t-designs for arbitrary, but large t, Cameron and Praeger proved the following result:

Theorem 1. ( [1] ) Let be a design. If acts block-transitively on, then, while if acts flag-transitively on, then.

Recently, Huber (see [2] ) completely classified all flag-transitive Steiner t-designs using the classification of the finite 2-transitive permutation groups. Hence the determination of all flag-transitive and block-transitive t-designs with has remained of particular interest and has been known as a long-standing and still open problem.

The present paper continues the work of classifying block-transitive t-designs. We discuss the block-transitive designs and Ree groups. We get the following result:

Main Theorem. Let be a non-trivial design, where for some positive integer, and is block-transitive. If, the socle of G, is, then G is not flag-transitive.

The second section describes the definitions and contains several preliminary results about flag-transitivity and t-designs. In 3 Section, we give the proof of the Main Theorem.

2. Preliminary Results

The Ree groups form an infinite family of simple groups of Lie type, and were defined in [3] as subgroups of. Let be finite field of q elements, where for some positive integer (in particular,). Let Q is a Sylow 3-subgroup of G, K is a multiplicative group of and is a group of order (see [4] - [6] ). Hence is a group of automorphisms of Steiner design and acts 2-transitive on points (see [7] ).

Here we gather notation which are used throughout this paper. For a t-design with, let r denotes the number of blocks through a given point, denotes the stabilizer of a point and the setwise stabilizer of a block. We define. For integers m and n, let denotes the greatest common divisor of m and n, and if m divides n.

Lemma 1. ( [2] ) Let G act flag-transitively on design. Then G is block-transitive and the following cases hold:

1), where;

2), where;

3), where.

Lemma 2. ( [8] ) Let is a non-trivial design. Then

Lemma 3. ( [8] ) Let is a non-trivial design. Then

1);

2).

Corollary 1. Let is a non-trivial design. If, Then.

Proof. By Lemma 2, we have. If, then

Hence

We get

3. Proof of the Main Theorem

Suppose that G acts flag-transitively on design and. Then G is block-transitive and point-transitive. Since, we may assume that and by Dedekind’s theorem, where, and a is an automorphism of field. Let, is odd, and, then. Obviously,.

First, we will proof that if fixes three different points of, then g must fix at least four points in.

Suppose that, ,. Let P is a normal Sylow 3-subgroup of. Then

is transitive on. By, we have. Hence P acts regularly on. There exist such that, where for all. Since, and P is a normal

Sylow 3-subgroup of, we have. On the other hand,

So, that is. Hence. We get that C is transitive on. Hence. By, we have. Note that, so . Hence. It follows that. This means that g must fix at least four points in.

Now, we can continue to prove our main theorem. Obviously, fixes three points of which are. Then. Hence must fix at least five points in. Since G acts block-transitively on design, we can find four blocks, let, , and, containing four points which is fixed by a. If a exchange, , and, then which is impossible. Thus a must fix, ,

and. We have. Therefore T acts also flag-transitively on design. We may assume and.

Since G acts flag-transitively on design, then G is point-transitive. By Lemma 1(1), we get

Again by Lemma 3(2) and Lemma 1(3),

Thus

By Lemma 2,

Again by Corollary 1,

This is impossible.

This completes the proof the Main Theorem.

Conflicts of Interest

The authors declare no conflicts of interest.

References