Ruijin Lou, Penghui Lv, Guoguang Lin^*
Mathematical of Yunnan University, Kunming, China.
DOI: 10.4236/ijmnta.2016.51008   PDF    HTML   XML   2,746 Downloads   3,709 Views   Citations

Abstract

In this paper, we consider a class of generalized nonlinear Kirchhoff-Sine-Gordon equation . By a priori estimation, we first prove the existence and uniqueness of solutions to the initial boundary value conditions, and then we study the global attractors of the equation.

Keywords

Kirchhoff-Sine-Gordon Equation, The Existence and Uniqueness of Solutions, Priori Estimates, Global Attractors

Share and Cite:

Received 29 December 2015; accepted 14 March 2016; published 17 March 2016

1. Introduction

In 1883, Kirchhoff [1] proposed the following model in the study of elastic string free vibration:

, where is associated with the initial tension, M is related to the material

properties of the rope, and indicates the vertical displacement at the x point on the t. The equation is more accurate than the classical wave equation to describe the motion of an elastic rod.

Masamro [2] proposed the Kirchhoff equation with dissipation and damping term:

where is a bounded domain of 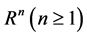with a smooth boundary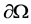; he uses the Galerkin method to prove the existence of the solution of the equation at the initial boundary conditions.

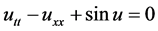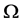Sine-Gordon equation is a very useful model in physics. In 1962, Josephson [3] fist applied the Sine-Gordon equation to superconductors, where the equation:, is the two-order partial derivative of u with respect to the variable t; is the two-order partial derivative of the u about the independent variable x. Subsequently, Zhu [4] considered the following problem: (where is a bounded domain of) and he proved the existence of the global solution of the equation. For more research on the global solutions and global attractors of Kirchhoff and sine-Gordon equations, we refer the reader to [5] -[11] .

Based on Kirchhoff and Sine-Gordon model, we study the following initial boundary value problem:

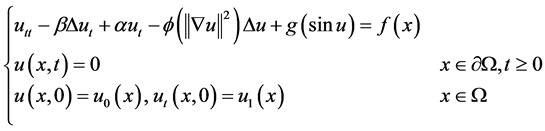(1.1)

where is a bounded domain of with a smooth boundary; is the dissipation coefficient; is a positive constant; and is the external interference. The assumptions on nonlinear terms and will be specified later.

The rest of this paper is organized as follows. In Section 2, we first obtain the basic assumption. In Section 3, we obtain a priori estimate. In Section 4, we prove the existence of the global attractors.

2. Basic Assumption

For brevity, we define the Sobolev space as follows:

In addition, we define and are the inner product and norm of H.

Nonlinear function satisfying condition (G):

(1)

(2)

(3)

Function satisfies the condition (F):

(4)

(5)

(6)

(7)

3. A Priori Estimates

Lemma 3.1. Assuming the nonlinear function satisfies the condition (G)-(F), , , then the solution of the initial boundary value problem (1.1) satisfies and

where. Thus there exists a positive constant and, such that

Proof. Let, the equation can be transformed into

(3.1)

Taking the inner product of the equations (3.1) with v in H, we find that

(3.2)

By using Holder inequality, Young’s inequality and Poincare inequality, we deal with the terms in (3.2) one by as follows

(3.3)

where is the first eigenvalue of with Dirichlet boundary conditions on.

Since and (F) (6), (7), we get

(3.4)

and

(3.5)

(3.6)

where

(3.7)

Combined (3.1)-(3.6) type, it follows from that

(3.8)

According to condition (F) (5), this will imply, then,

, and since

(3.9)

that is

(3.10)

With (3.10), (3.8) can be written as

(3.11)

Set, and, then (3.11) is equivalent to (3.12)

(3.12)

where

(3.13)

By using Gronwall inequality, we obtain

(3.14)

Let.

So, we have

(3.15)

then

(3.16)

Hence, there exists and, such that

■

Lemma 3.2. Assuming the nonlinear function satisfies the condition (G)-(F), , then the solution of satisfies the initial boundary value problem (1.1) satisfies and

where. Thus there exists a positive constant and, such that

Proof. The equations (3.1) in the H and have inner product, we find that

(3.17)

By using Holder inequality, Young’s inequality and Poincare inequality, we get the following results

(3.18)

(3.19)

According to condition (F) (5), (6), we obtain

(3.20)

(3.21)

where

(3.22)

By (3.18)-(3.22), (3.17) can be written

(3.23)

Noticing, this will imply

(3.24)

Substituting (3.24) into (3.23), we can get the following inequality

(3.25)

Let, and, then (3.25) type can be changed into

(3.26)

then

(3.27)

where.

By using Gronwall inequality, we obtain

(3.28)

taking, we have

(3.29)

then

(3.30)

Hence, there exists and, such that

■

Theorem 3.1. Assuming the nonlinear function satisfies the condition (G)-(F), , , so the initial boundary value problem (1.1) exists a unique smooth solution.

Proof. By Lemma 3.1-Lemma 3.2 and Glerkin method, we can easily obtain the existence of solutions of equ-

ation, the proof procedure is omitted. Next, we prove the uniqueness of solutions in

detail.

Assume are two solutions of equation, we denote, then, the two equations subtract and obtain

(3.31)

We take the inner product of the above equations (3.31) with in H, we have

(3.32)

We deal with the terms in (3.32) one by as follows

(3.33)

and

(3.34)

By (3.32)-(3.34), we can get the following inequality

(3.35)

Further, by mid-value theorem and Young’s inequality, we get

(3.36)

Since,

might as well set.

where.

Then, we obtain

(3.37)

Substituting (3.36), (3.37) into (3.35), we can get

(3.38)

Let, then (3.38) can be changed to

(3.39)

By using Gronwall inequality, we obtain

(3.40)

There has

(3.41)

That show that.

So as to get, the uniqueness is proved. ■

4. Global Attractor

Theorem 4.1. [12] Set be a Banach space, and are the semigroup operator on.; here I is a unit operator. Set satisfy the follow conditions.

1) is bounded, namely; it exists a constant, so that

2) It exists a bounded absorbing set, namely,; it exists a constant, so that

here and B are bounded sets.

3) When, is a completely continuous operator.

Therefore, the semigroup operators S(t) exist a compact global attractor A.

Theorem 4.2. [12] Under the assume of Theorem 3.1, equations have global attractor

where; is the bounded absorbing set of and satisfies

(1);

(2), here and it is a bounded set, .

Proof. Under the conditions of Theorem 3.1, it exists the solution semigroup S(t), here .

(1) From Lemma 3.1-Lemma 3.2, we can get that is a bounded set that includes in the ball,

This shows that is uniformly bounded in.

(2) Furthermore, for any, when, we have

So we get is the bounded absorbing set.

(3) Since is compact embedded, which means that the bounded set in is the compact set in, so the semigroup operator S(t) is completely continuous. ■

Hence, the semigroup operator S(t) exists a compact global attractor A. The proving is completed.

Acknowledgements

The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.

Funding

This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Kirchhof, G. (1883) Vorlesungen fiber Mechanik. Teubner, Stuttgarty.
[2]	Masamro, H. and Yoshio, Y. (1991) On Some Nonlinear Wave Equations 2: Global Existence and Energy Decay of Solutions. J. Fac. Sci. Univ. Tokyo. Sect. IA, Math., 38, 239-250.
[3]	Josephson, B.D. (1962) Possible New Effects in Superconductive Tunneling. Physics Letters, 1, 251-253. http://dx.doi.org/10.1016/0031-9163(62)91369-0
[4]	Zhu, Z.W. and Lu, Y. (2000) The Existence and Uniqueness of Solution for Generalized Sine-Gordon Equation. Chinese Quarterly Journal of Mathematics, 15, 71-77.
[5]	Li, Q.X. and Zhong, T. (2002) Existence of Global Solutions for Kirchhoff Type Equations with Dissipation and Damping Terms. Journal of Xiamen University: Natural Science Edition, 41, 419-422.
[6]	Silva, M.A.J. and Ma, T.F. (2013) Long-Time Dynamics for a Class of Kirchhoff Models with Memory. Journal of Mathematical Physics, 54, Article ID: 021505.
[7]	Zhang, J.W., Wang, D.X. and Wu, R.H. (2008) Global Solutions for a Class of Generalized Strongly Damped Sine-Gordon Equation. Journal of Mathematical Physics, 57, 2021-2025.
[8]	Guo, L., Yuan, Z.Q. and Lin, G.G. (2014) The Global Attractors for a Nonlinear Viscoelastic Wave Equation with Strong Damping and Linear Damping and Source Terms. International Journal of Modern Nonlinear Theory and Application, 4, 142-152. http://dx.doi.org/10.4236/ijmnta.2015.42010
[9]	Teman, R. (1988) Infiniter-Dimensional Dynamical Systems in Mechanics and Physics. Springer-Verlag, New York, 15-26. http://dx.doi.org/10.1007/978-1-4684-0313-8_2
[10]	Ma, Q.F., Wang, S.H. and Zhong, C.K. (2002) Necessary and Sufficient Congitions for the Existence of Global Attractors for Semigroup and Applications. Indiana University Mathematics Journal, 51, 1541-1559. http://dx.doi.org/10.1512/iumj.2002.51.2255
[11]	Ma, Q.Z., Sun, C.Y. and Zhong, C.K. (2007) The Existence of Strong Global Attractors for Nonlinear Beam Equations. Journal of Mathematical Physics, 27A, 941-948.
[12]	Lin, G.G. (2011) Nonlinear Evolution Equation. Yunnan University Press, 12.