Received 26 October 2015; accepted 5 December 2015; published 8 December 2015


1. Introduction
The interaction of fiscal and monetary policy is a major issue in macroeconomic theory (e.g., Leeper [1] ; Woodford [2] ; Canzoneri, Cumby, and Diba [3] ), but still under-explored in open-economy environments. The central contributions of this paper are to present a theoretical investigation on the dynamic effects of fiscal and monetary feedback policy rules in a small open economy with flexible exchange rates―whereby external debt is subject to credit risk, consistently with empirical evidence (e.g., Montiel [4] )―and point out new analytical results that would not appear in closed-economy frameworks.
Specifically, we show that determinacy of equilibrium is verified only under locally Ricardian fiscal policies―whereby the setting of primary budget surpluses guarantees per se the stability of government liabilities in the neighborhood of the steady state (see Woodford [2] )―irrespectively of stance of monetary policy. This result is in contrast with traditional closed-economy environments, in which uniqueness and stability of equilibrium require locally Ricardian fiscal policies in conjunction with interest rate policies overreacting to inflation (e.g. Leeper [1] ; Woodford [2] ).
In particular, we show that fiscal revaluation mechanisms of the type predicted by the fiscal theory of the price level (see Leeper and Yun [5] )―involving endogenous inflation jumps that stabilize in equilibrium real government liabilities―cannot take place because they are ruled out by international parity conditions precluding arbitrage opportunities. Consequently, it emerges that locally non-Ricardian fiscal policies are destabilizing even under an accommodating monetary policy stance.
The paper is organized as follows. Section 2 presents the dynamic model. Section 3 examines equilibrium dynamics and derives the main results. Section 4 concludes.
2. The Model
Consider the following extension of the continuous-time closed-economy monetary framework set out by Benhabib, Schmitt-Grohé and Uribe [6] to an open-economy environment. Assume a small open economy which produces and consumes tradeable and perishable goods. Purchasing power parity (PPP) implies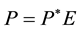 , where
, where  is the domestic (foreign) price level and E is the nominal exchange rate. In percentage terms,
is the domestic (foreign) price level and E is the nominal exchange rate. In percentage terms,
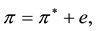 (1)
(1)
where 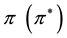 is the domestic (foreign) inflation rate and e is the rate of exchange depreciation of domestic currency.
is the domestic (foreign) inflation rate and e is the rate of exchange depreciation of domestic currency.
The asset menu for the domestic economy consists of domestic money, domestic government bonds and foreign assets. Domestic money and government bonds are not held by foreigners, whereas foreign assets are internationally-traded and are denominated in foreign currency. The world capital market is imperfect. In particular, the home country faces an upward-sloping supply curve of foreign debt, following Bardhan [7] , Obstfeld [8] , Bhandari, Haque and Turnovsky [9] , and Turnovsky [10] :
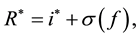 (2)
(2)
where 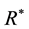 is the nominal interest rate on foreign debt,
is the nominal interest rate on foreign debt, 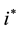 is the interest rate that prevails in the world market, f is the stock of real foreign debt, and
is the interest rate that prevails in the world market, f is the stock of real foreign debt, and 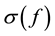 is the country-specific risk premium. Function
is the country-specific risk premium. Function 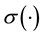 is continuous, increasing, and strictly positive. International capital mobility implies the following risk-adjusted interest parity:
is continuous, increasing, and strictly positive. International capital mobility implies the following risk-adjusted interest parity:
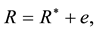 (3)
(3)
where R is the nominal rate of interest on bonds issued by the domestic government.
The representative household’s lifetime utility function is given by
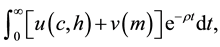 (4)
(4)
where 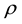 is the rate of time preferences and
is the rate of time preferences and 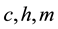 are consumption, labor and real money balances, respectively. Functions
are consumption, labor and real money balances, respectively. Functions 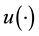 and
and 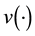 obey
obey ![]()
![]()
![]()
![]()
![]()
![]() and
and![]() . The instant flow budget constraint in real terms is given by
. The instant flow budget constraint in real terms is given by
![]() (5)
(5)
where ![]() denotes foreign assets, b government bonds, w the wage rate, z profits, and
denotes foreign assets, b government bonds, w the wage rate, z profits, and ![]() lump-sum taxes net of public transfers. Ponzi’s games are precluded. Since atomistic agents take the rate at which the country can borrow from abroad,
lump-sum taxes net of public transfers. Ponzi’s games are precluded. Since atomistic agents take the rate at which the country can borrow from abroad, ![]() , as given, optimality yields
, as given, optimality yields
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
where ![]() is the costate variable associated with the wealth accumulation Equation (5).
is the costate variable associated with the wealth accumulation Equation (5).
Perfectly competitive firms face the production function
![]() (12)
(12)
where y denotes output, ![]() ,
,![]() . Profit maximization implies
. Profit maximization implies![]() .
.
The domestic government’s flow budget constraint in real terms can be expressed as
![]() (13)
(13)
where ![]() denotes real government liabilities, and
denotes real government liabilities, and ![]() is the primary surplus inclusive of interest savings from the issuance of money, where g denotes public spending, assumed to be exogenous for simplicity.
is the primary surplus inclusive of interest savings from the issuance of money, where g denotes public spending, assumed to be exogenous for simplicity.
Consistently with Leeper [1] , the fiscal authority adjusts the primary surplus according to a feedback policy of the form
![]() (14)
(14)
where function ![]() is continuous, non-decreasing, and there exists at least one
is continuous, non-decreasing, and there exists at least one ![]() such that
such that![]() . In Woodford’s [2] terminology, fiscal policy is locally Ricardian (locally non-Ricardian) if
. In Woodford’s [2] terminology, fiscal policy is locally Ricardian (locally non-Ricardian) if![]() , yielding local stability (instability) of real government liabilities for all stable paths of the other endogenous variables.
, yielding local stability (instability) of real government liabilities for all stable paths of the other endogenous variables.
The monetary authority adopts an interest rate feedback rule of the form
![]() (15)
(15)
where ![]() is continuous, non-decreasing, and there exists at least one
is continuous, non-decreasing, and there exists at least one ![]() such that
such that![]() . The interest rate rule (15) satisfies the Taylor [11] principle if
. The interest rate rule (15) satisfies the Taylor [11] principle if![]() , that is, in the case in which the central bank responds to inflation by increasing the real interest rate.
, that is, in the case in which the central bank responds to inflation by increasing the real interest rate.
The law of motion of net foreign debt is given by the trade deficit plus interest payments:
![]() (16)
(16)
3. Equilibrium Dynamics
Combining the optimality conditions (6)-(10) with the risk-premium Equation (2), the international parity conditions (1) and (3), the production function (12), the domestic government debt accumulation Equation (13), the fiscal rule (14), the monetary rule (15), and the foreign debt accumulation Equation (16), the perfect-foresight equilibrium can be expressed as
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
![]() (20)
(20)
with![]() ,
,
![]() (21)
(21)
with![]() .
.
In the steady state, ![]() Thus, from (17)-(21), it must be
Thus, from (17)-(21), it must be ![]()
![]() and
and ![]() Linearizing the differential Equations (17)-(19) around the steady-state equilibrium
Linearizing the differential Equations (17)-(19) around the steady-state equilibrium ![]() yields
yields
![]() (22)
(22)
The equilibrium system (22) exhibits one jumping variable, ![]() , and two predetermined variables,
, and two predetermined variables, ![]() and f. Therefore, saddle-path stability requires that the associated Jacobian displays two negative eigenvalues and one positive eigenvalue.
and f. Therefore, saddle-path stability requires that the associated Jacobian displays two negative eigenvalues and one positive eigenvalue.
Explore the properties of the Jacobian matrix. Notice that one eigenvalue is![]() , so that a sufficient condition for equilibrium determinacy is to have a positive determinant of the Jacobian. Notice that the deter-
, so that a sufficient condition for equilibrium determinacy is to have a positive determinant of the Jacobian. Notice that the deter-
minant is ![]() if
if![]() . Consequently, a unique and stable equilibrium always requires a locally Ricardian fiscal policy, that is,
. Consequently, a unique and stable equilibrium always requires a locally Ricardian fiscal policy, that is,![]() . Whether monetary policy overreacts or underreacts to inflation is irrelevant for equilibrium determinacy.
. Whether monetary policy overreacts or underreacts to inflation is irrelevant for equilibrium determinacy.
By contrast, when fiscal policy is locally non-Ricardian, that is, ![]() , the determinant is negative and the trace,
, the determinant is negative and the trace, ![]() , is positive. In this case, instability always occurs, because we have one negative eigenvalue and two positive eigenvalues. In such circumstances, passive monetary policies, even including interest rate pegs, are not sufficient to pin down unique and stable equilibrium paths.
, is positive. In this case, instability always occurs, because we have one negative eigenvalue and two positive eigenvalues. In such circumstances, passive monetary policies, even including interest rate pegs, are not sufficient to pin down unique and stable equilibrium paths.
4. Conclusions
In this paper we have analyzed macroeconomic dynamics induced by fiscal and monetary feedback policies in the context of a continuous-time optimizing model of a small open economy facing an imperfect global capital market. In particular, consistent with the empirical evidence, the framework of analysis features a risk premium on external debt influencing the transmission mechanism of policy rules.
Our major findings can be summarized as follows. In contrast with closed-economy models, we have demonstrated that the existence of a unique and stable equilibrium requires locally Ricardian fiscal policies regardless of the degree of feedback of nominal interest rates to inflationary pressures. We have shown, in particular, that international parity conditions excluding arbitrage opportunities rule out the possibility of endogenous jumps in the inflation rate―along the lines depicted by the fiscal theory of the price level―capable to stabilize real government liabilities. Therefore, locally non-Ricardian fiscal policies are not sufficient to avoid macroeconomic instability even if the central bank follows passive monetary policies.
Acknowledgements
I am grateful to Paolo Canofari and Michele Postigliola for useful remarks and discussions. The usual disclaimers apply. I would like to thank an anonymous referee for helpful comments and suggestions.