The Relation between the Stabilization Problem for Discrete Event Systems Modeled with Timed Petri Nets via Lyapunov Methods and Max-Plus Algebra ()
1. Introduction
A discrete event system, is a dynamical system whose state evolves in time by the occurrence of events at possibly irregular time intervals. Timed Petri nets are a graphical and mathematical modeling tool applicable to discrete event systems in order to represent its states evolution where the timing at which the state changes is taken into consideration Timed Petri nets are known to be useful for analyzing the systems properties in addition of being a paradigm for describing and studying information processing systems, where the timing at which the state changes is taken into consideration. For a detailed discussion of Petri net theory see [1] and the references quoted therein. One of the most important performance issues to be considered in a discrete event system is its stability. Lyapunov theory provides the required tools needed to aboard the stability and stabilization problems for discrete event systems modeled with timed Petri nets whose mathematical model is given in terms of difference equations [2]. By proving stability one guarantees a bound on the discrete event systems state dynamics. When the system is unstable, a sufficient condition to stabilize the system is given. It is shown that it is possible to restrict the discrete event systems state space in such a way that boundedness is achieved. However, the restriction is not numerically precisely known. This inconvenience is overcome by considering a specific recurrence equation, in the max-plus algebra, which is assigned to the timed Petri net graphical model. This paper proposes a methodology consisting in combining Lyapunov theory with max-plus algebra to give a precise solution to the stabilization problem for discrete event systems modeled with timed Petri nets. The presented methodology results to be innovative and it is not, in general, known. The main objective of the paper is to spread its results along large audiences. The paper is organized as follows. In Section 2, Lyapunov theory for discrete event systems modeled with Petri nets is given. Section 3 presents max-plus algebra and max-plus recurrence equations for timed event Petri nets. Section 4 considers the solution to the stabilization problem for discrete event systems modeled with timed Petri nets. Finally, the paper ends with some conclusions.
2. Lyapunov Stability and Stabilization of Discrete Event Systems Modeled with Petri Nets [2]-[4]
NOTATION: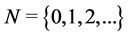 ,
, 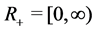 ,
,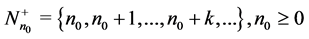 . Given
. Given ,
, 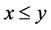 is equivalent to
is equivalent to . A function
. A function ,
,  is called nondecreasing in
is called nondecreasing in 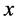 if given
if given  such that
such that 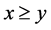 and
and 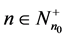 then,
then, . Consider systems of first ordinary difference equations given by
. Consider systems of first ordinary difference equations given by
 (1)
(1)
where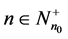 ,
,  and
and 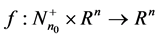 is continuous in
is continuous in![]() .
.
Definition 1 The ![]() vector valued function
vector valued function ![]() is said to be a solution of (1) if
is said to be a solution of (1) if ![]() and
and ![]() for all
for all![]() .
.
Definition 2 The system (1) is said to be practically stable, if given ![]() with
with![]() , then
, then ![]()
Definition 3 A continuous function ![]() is said to belong to class
is said to belong to class ![]() if
if ![]() and it is strictly increasing.
and it is strictly increasing.
Consider a vector Lyapunov function![]() ,
, ![]() and define the variation of
and define the variation of ![]() relative to (1) by
relative to (1) by
![]() (2)
(2)
Theorem 4 Let ![]() be a continuous function in
be a continuous function in![]() , define the function
, define the function ![]() such that satisfies the estimates
such that satisfies the estimates
![]() (3)
(3)
for![]() ,
, ![]() , where
, where ![]() is a continuous function in the second argument. Assume
is a continuous function in the second argument. Assume
that: ![]() is nondecreasing in
is nondecreasing in![]() ,
, ![]() are given and finally that
are given and finally that ![]() is satisfied. Then, the practical stability properties of
is satisfied. Then, the practical stability properties of
![]() (4)
(4)
imply the practical stability properties of system (1).
Corollary 5 In Theorem (4): If ![]() we get uniform practical stability of (1) which implies structural stability.
we get uniform practical stability of (1) which implies structural stability.
Definition 6 A Petri net is a 5-tuple, ![]() where:
where: ![]() is a finite set of places,
is a finite set of places, ![]() is a finite set of transitions,
is a finite set of transitions, ![]() is a set of arcs,
is a set of arcs, ![]() is a weight function,
is a weight function,![]() :
: ![]() is the initial marking,
is the initial marking, ![]() and
and![]() .
.
Definition 7 The clock structure associated with a place ![]() is a set
is a set ![]() of clock sequences
of clock sequences ![]()
![]()
![]()
The positive number![]() , associated to
, associated to![]() , called holding time, represents the time that a token must spend in this place until its outputs enabled transitions
, called holding time, represents the time that a token must spend in this place until its outputs enabled transitions ![]() fire. We partition
fire. We partition ![]() into subsets
into subsets ![]() and
and![]() , where
, where ![]() is the set of places with zero holding time, and
is the set of places with zero holding time, and ![]() is the set of places that have some holding time.
is the set of places that have some holding time.
Definition 8 A timed Petri net is a 6-tuple ![]() where
where ![]() are as before, and
are as before, and ![]() is a clock structure. A timed Petri net is a timed event petri net when every
is a clock structure. A timed Petri net is a timed event petri net when every ![]() has one input and one output transition, in which case the associated clock structure set of a place
has one input and one output transition, in which case the associated clock structure set of a place ![]() reduces to one element
reduces to one element![]() .
.
Notice that if ![]() (or
(or![]() ) then, this is often represented graphically by
) then, this is often represented graphically by![]() , (
, (![]() ) arcs from
) arcs from ![]() to
to ![]() (
(![]() to
to![]() ) each with no numeric label.
) each with no numeric label.
Let ![]() denote the marking (i.e., the number of tokens) at place
denote the marking (i.e., the number of tokens) at place ![]() at time
at time ![]() and let
and let ![]() denote the marking (state) of
denote the marking (state) of ![]() at time
at time![]() . A transition
. A transition ![]() is said to be enabled at time
is said to be enabled at time ![]() if
if ![]() for all
for all ![]() such that
such that![]() . It is assumed that at each time
. It is assumed that at each time ![]() there exists at least one transition to fire. If a transition is enabled then, it can fire. If an enabled transition
there exists at least one transition to fire. If a transition is enabled then, it can fire. If an enabled transition ![]() fires at time
fires at time ![]() then, the next marking for
then, the next marking for ![]() is given by
is given by
![]() (5)
(5)
Let ![]() denote an
denote an ![]() matrix of integers (the incidence matrix) where
matrix of integers (the incidence matrix) where ![]() with
with ![]() and
and![]() . Let
. Let ![]() denote a firing vector where if
denote a firing vector where if ![]() is fired then, its
is fired then, its
corresponding firing vector is ![]() with the one in the
with the one in the ![]() position in the vector and zeros everywhere else. The nonlinear difference matrix equation describing the dynamical behavior represented by a
position in the vector and zeros everywhere else. The nonlinear difference matrix equation describing the dynamical behavior represented by a ![]() is:
is:
![]() (6)
(6)
where if at step![]() ,
, ![]() for all
for all ![]() then,
then, ![]() is enabled and if this
is enabled and if this ![]() fires then, its corresponding firing vector
fires then, its corresponding firing vector ![]() is utilized in the difference equation to generate the next step. Notice that if
is utilized in the difference equation to generate the next step. Notice that if ![]() can be reached from some other marking
can be reached from some other marking ![]() and, if we fire some sequence of
and, if we fire some sequence of ![]() transitions with corresponding firing vectors
transitions with corresponding firing vectors ![]() we obtain that
we obtain that
![]() (7)
(7)
Let ![]() be a metric space where
be a metric space where ![]() is defined by
is defined by ![]() and consider the matrix difference equation which describes the dynamical behavior of the discrete event system modeled by a
and consider the matrix difference equation which describes the dynamical behavior of the discrete event system modeled by a![]() , see (7).
, see (7).
Proposition 9 Let ![]() be a Petri net.
be a Petri net. ![]() is uniform practical stable if there exists a
is uniform practical stable if there exists a ![]() strictly positive
strictly positive ![]() vector such that
vector such that
![]() (8)
(8)
Moreover, ![]() is uniform practical asymptotic stable if the following equation holds
is uniform practical asymptotic stable if the following equation holds
![]() (9)
(9)
Lemma 10 Let suppose that Proposition (9) holds then,
![]() (10)
(10)
Remark 11 Notice that since the state space of a TPN is contained in the state space of the same now not timed PN, stability of PN implies stability of the TPN.
Lyapunov Stabilization
Definition 12 Let ![]() be a Petri net.
be a Petri net. ![]() is said to be stabilizable if there exists a firing transition sequence with transition count vector
is said to be stabilizable if there exists a firing transition sequence with transition count vector ![]() such that system (7) remains bounded.
such that system (7) remains bounded.
Proposition 13 Let ![]() be a Petri net.
be a Petri net. ![]() is stabilizable if there exists a firing transition sequence with transition count vector
is stabilizable if there exists a firing transition sequence with transition count vector ![]() such that the following equation holds
such that the following equation holds
![]() (11)
(11)
Remark 14 By fixing a particular![]() , which satisfies (11), the state space is restricted to those markings that are finite.
, which satisfies (11), the state space is restricted to those markings that are finite.
3. Max-Plus Algebra [5] [6]
3.1. Basic Definitions
NOTATION:![]() ,
, ![]() ,
,![]()
![]() . Let
. Let ![]() and define the operations
and define the operations ![]() and
and ![]() by:
by: ![]() and
and![]() .
.
Definition 15 The set ![]() with the two operations
with the two operations ![]() and
and ![]() is called a max-plus algebra and is denoted by
is called a max-plus algebra and is denoted by ![]()
Definition 16 A semiring is a nonempty set ![]() endowed with two operations
endowed with two operations ![]()
![]() and two elements
and two elements ![]() and
and ![]() such that:
such that: ![]() is associative and commutative with zero element
is associative and commutative with zero element ![]()
![]() is associative, distributes over
is associative, distributes over![]() , and has unit element
, and has unit element ![]()
![]() is absorbing for
is absorbing for ![]() i.e.,
i.e., ![]() ,
, ![]() In addition if
In addition if ![]() is commutative then
is commutative then ![]() is called a commutative semiring, and if
is called a commutative semiring, and if ![]() is such that
is such that![]() ,
, ![]() then it is called idempotent.
then it is called idempotent.
Theorem 17 The max-plus algebra ![]() has the algebraic structure of a commutative and idempotent semiring.
has the algebraic structure of a commutative and idempotent semiring.
3.2. Matrices and Graphs
Let ![]() be the set of
be the set of ![]() matrices with coefficients in
matrices with coefficients in ![]() with the following operations: The sum of matrices
with the following operations: The sum of matrices![]() , denoted
, denoted ![]() is defined by:
is defined by: ![]() for
for ![]() and
and ![]()
The product of matrices![]() , denoted
, denoted ![]() is defined by:
is defined by: ![]() for
for ![]()
and![]() . Let
. Let ![]() denote the matrix with all its elements equal to
denote the matrix with all its elements equal to ![]() and denote by
and denote by ![]() the matrix which has its diagonal elements equal to
the matrix which has its diagonal elements equal to ![]() and all the other elements equal to
and all the other elements equal to ![]() Then, the following result can be stated.
Then, the following result can be stated.
Theorem 18 The 5-tuple ![]() has the algebraic structure of a noncommutative idempotent semiring.
has the algebraic structure of a noncommutative idempotent semiring.
Definition 19 Let ![]() and
and ![]() then the k-th power of
then the k-th power of ![]() denoted by
denoted by ![]() is defined by:
is defined by: ![]() (k times), where
(k times), where ![]() is set equal to
is set equal to![]() .
.
Definition 20 A matrix ![]() is said to be regular if
is said to be regular if ![]() contains at least one element distinct from
contains at least one element distinct from ![]() in each row.
in each row.
Definition 21 Let ![]() be a finite and non-empty set and consider
be a finite and non-empty set and consider![]() . The pair
. The pair ![]() is called a directed graph, where
is called a directed graph, where ![]() is the set of elements called nodes and
is the set of elements called nodes and ![]() is the set of ordered pairs of nodes called arcs. A directed graph
is the set of ordered pairs of nodes called arcs. A directed graph ![]() is called a weighted graph if a weight
is called a weighted graph if a weight ![]() is associated with any arc
is associated with any arc![]() .
.
Let ![]() be any matrix, a graph
be any matrix, a graph![]() , called the communication graph of
, called the communication graph of![]() , can be associated as follows. Define
, can be associated as follows. Define ![]() and a pair
and a pair ![]() will be a member of
will be a member of![]() , where
, where ![]() denotes the set of arcs of
denotes the set of arcs of![]() .
.
Definition 22 A path from node ![]() to node
to node ![]() is a sequence of arcs
is a sequence of arcs ![]() such that
such that![]() , for
, for ![]() and
and![]() . The path
. The path ![]() consists of the nodes
consists of the nodes ![]() with length
with length ![]() denoted by
denoted by![]() . In the case when
. In the case when ![]() the path is said to be a circuit. A circuit is said to be elementary if nodes
the path is said to be a circuit. A circuit is said to be elementary if nodes ![]() and
and ![]() are different for
are different for![]() . A circuit consisting of one arc is called a self-loop.
. A circuit consisting of one arc is called a self-loop.
Let us denote by ![]() the set of all paths from node
the set of all paths from node ![]() to node
to node ![]() of length
of length ![]() and for any arc
and for any arc ![]() let its weight be given by
let its weight be given by ![]() then the weight of a path
then the weight of a path ![]() denoted by
denoted by ![]() is defined to be the sum of the weights of all the arcs that belong to the path. The average weight of a path
is defined to be the sum of the weights of all the arcs that belong to the path. The average weight of a path ![]() is given by
is given by![]() . Given two paths, as for example,
. Given two paths, as for example, ![]() and
and ![]() in
in ![]() the concatenation of paths
the concatenation of paths ![]() is defined as
is defined as![]() . The communication graph
. The communication graph ![]() and powers of matrix
and powers of matrix ![]() are closely related as it is shown in the next theorem.
are closely related as it is shown in the next theorem.
Theorem 23 Let![]() , then
, then![]() :
:![]() , where
, where ![]() in the case when
in the case when ![]() is empty i.e., no path of length
is empty i.e., no path of length ![]() from node
from node ![]() to node
to node ![]() exists in
exists in![]() .
.
Definition 24 Let ![]() then define the matrix
then define the matrix ![]() as:
as:![]() . Where the element
. Where the element ![]() gives the maximal weight of any path from
gives the maximal weight of any path from ![]() to
to![]() . If in addition one wants to add the possibility of staying at a node then one must include matrix
. If in addition one wants to add the possibility of staying at a node then one must include matrix ![]() in the definition of matrix
in the definition of matrix ![]() giving rise to its Kleene star representation defined by:
giving rise to its Kleene star representation defined by: ![]()
Lemma 25 Let ![]() be such that any circuit in
be such that any circuit in ![]() has average circuit weight less than or equal to
has average circuit weight less than or equal to![]() . Then it holds that:
. Then it holds that: ![]()
Definition 26 Let ![]() be a graph and
be a graph and![]() , node
, node ![]() is reachable from node
is reachable from node![]() , denoted as
, denoted as![]() , if there exists a path from
, if there exists a path from ![]() to
to![]() . A graph
. A graph ![]() is said to be strongly connected if
is said to be strongly connected if![]() . A matrix
. A matrix ![]() is called irreducible if its communication graph is strongly connected, when this is not the case matrix
is called irreducible if its communication graph is strongly connected, when this is not the case matrix ![]() is called reducible.
is called reducible.
Remark 27 In this paper irreducible matrices are just considered. It is possible to treat the reducible case by transforming it into its normal form and computing its generalized eigenmode see [5].
Spectral Theory and Linear Equations
Definition 28 Let ![]() be a matrix. If
be a matrix. If ![]() is a scalar and
is a scalar and ![]() is a vector that contains at least one finite element such that:
is a vector that contains at least one finite element such that: ![]() then,
then, ![]() is called an eigenvalue and
is called an eigenvalue and ![]() an eigenvector.
an eigenvector.
Let ![]() denote the set of all elementary circuits in
denote the set of all elementary circuits in ![]() and write:
and write: ![]() for the maximal
for the maximal
average circuit weight. Notice that since ![]() is a finite set, the maximum is attained (which is always the case when matrix
is a finite set, the maximum is attained (which is always the case when matrix ![]() is irreducible). In case
is irreducible). In case ![]() define
define![]() .
.
Definition 29 A circuit ![]() is said to be critical if its average weight is maximal. The critical graph of
is said to be critical if its average weight is maximal. The critical graph of![]() , denoted by
, denoted by![]() , is the graph consisting of those nodes and arcs that belong to critical circuits in
, is the graph consisting of those nodes and arcs that belong to critical circuits in![]() .
.
Theorem 30 If ![]() is irreducible, then there exists one and only one finite eigenvalue (with possible several eigenvectors). This eigenvalue is equal to the maximal average weight of circuits in
is irreducible, then there exists one and only one finite eigenvalue (with possible several eigenvectors). This eigenvalue is equal to the maximal average weight of circuits in ![]()
![]() .
.
Theorem 31 Let ![]() and
and![]() . If the communication graph
. If the communication graph ![]() has maximal average circuit
has maximal average circuit
weight less than or equal to![]() , then
, then ![]() solves the equation
solves the equation![]() . Moreover, if the circuit weights in
. Moreover, if the circuit weights in ![]() are negative then, the solution is unique.
are negative then, the solution is unique.
3.3. Max-Plus Recurrence Equations for Timed Event Petri Nets
Definition 32 Let ![]() for
for ![]() and
and ![]() for
for![]() ;
;![]() . Then, the recurrence equation:
. Then, the recurrence equation: ![]() is called an Mth order recurrence equation.
is called an Mth order recurrence equation.
Theorem 33 The Mth order recurrence equation, given by equation![]() , can be transformed into a first order recurrence equation
, can be transformed into a first order recurrence equation![]() ;
; ![]() provided that
provided that ![]() has circuit weights less than or equal to zero.
has circuit weights less than or equal to zero.
With any timed event Petri net, matrices ![]() can be defined by setting
can be defined by setting![]() , where
, where ![]() is the largest of the holding times with respect to all places between transitions
is the largest of the holding times with respect to all places between transitions ![]() and
and ![]() with
with ![]() tokens, for
tokens, for![]() , with
, with ![]() equal to the maximum number of tokens with respect to all places. Let
equal to the maximum number of tokens with respect to all places. Let ![]() denote the kth time that transition
denote the kth time that transition ![]() fires, then the vector
fires, then the vector![]() , called the
, called the
state of the system, satisfies the Mth order recurrence equation:![]() . Now, assuming that all the hypothesis of theorem (33) are satisfied, and setting
. Now, assuming that all the hypothesis of theorem (33) are satisfied, and setting![]() , equation
, equation ![]() can be expressed as:
can be expressed as:![]() , which is known as the standard autonomous equation.
, which is known as the standard autonomous equation.
4. The Solution to the Stability Problem for Discrete Event Dynamical Systems Modeled with Timed Petri Nets
Definition 34 A TPN is said to be stable if all the transitions fire with the same proportion i.e., if there exists ![]() such that
such that
![]() (12)
(12)
This means that in order to obtain a stable ![]() all the transitions have to be fired
all the transitions have to be fired ![]() times. It will be desirable to be more precise and know exactly how many times. The answer to this question is given next.
times. It will be desirable to be more precise and know exactly how many times. The answer to this question is given next.
Lemma 35 Consider the recurrence relation![]() ,
, ![]() arbitrary.
arbitrary. ![]() an irreducible matrix and
an irreducible matrix and ![]() its eigenvalue then,
its eigenvalue then,
![]() (13)
(13)
Proof. Let ![]() be an eigenvector of
be an eigenvector of ![]() such that
such that ![]() then,
then,
![]()
Now starting with an unstable![]() , collecting the results given by: proposition (13), what has just been discussed about recurrence equations for
, collecting the results given by: proposition (13), what has just been discussed about recurrence equations for ![]() at the end of subsection (3.3) and the previous lemma (35) plus theorem (30), the solution to the problem is obtained.
at the end of subsection (3.3) and the previous lemma (35) plus theorem (30), the solution to the problem is obtained.
5. Conclusion
The main objective of the proposal is to make it knowledgeable to large audiences. This paper gives a complete and precise solution to the stabilization problem for discrete event systems modeled with timed Petri nets combining Lyapunov theory with max-plus algebra. The presented methodology results to be innovative.