1. Introduction
Two finite masses, called primaries, are moving in circular orbits around their common centre of mass, and an infinitesimal mass is moving in the plane of motion of the primaries. To study the motion of the infinitesimal mass is called the restricted three body problem. [1] proved that there existed five points of equilibrium, or points of libration (often denoted by L1, ….. L5), which were the stationary solutions of the restricted problem. Out of them, three are collinear and two are non collinear. The collinear libration points are unstable for all values of mass parameter 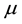 and the triangular libration points are stable for
and the triangular libration points are stable for , where
, where  is a critical value of mass parameter [2] .
is a critical value of mass parameter [2] .
As we know, dissipative forces are those where there is a loss of energy such as friction and one of the most important mechanisms of dissipation is the Stokes drag which is a force experienced by a particle moving in a gas, due to the collisions of the particle with the molecules of the gas.
[3] has determined some results on the global dynamics of the regularized restricted three body problem with dissipative forces. Their investigations have motivated us to study the motion of the restricted three body problem under dissipative forces such as Stokes drag. In the synodic frame, Stokes drag force is defined by [4] :
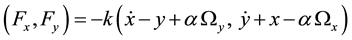
where 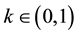 is the dissipative constant, depending on several physical parameters like the viscosity of the gas, the radius and mass of the particle. Here
is the dissipative constant, depending on several physical parameters like the viscosity of the gas, the radius and mass of the particle. Here

is the keplerian angular velocity at distance  from the origin of the synodic frame and
from the origin of the synodic frame and  is the ratio between the gas and keplerian velocities.
is the ratio between the gas and keplerian velocities.
A number of authors have investigated the location and stability of the equilibrium point in the presence of specific dissipative forces. [5] has used the Jacobi constant to investigate the effect of an external drag force proportional to the velocity in the rotating frame and has concluded that L4 and L5 are unstable to this type of drag force. In their studies of the motion of dust particles in the vicinity of the Earth, [6] has analyzed the stability of the equilibrium points in the presence of radiation pressure which includes the Poynting Robertson drag terms. They have shown that the libration points are unstable to such a drag force. The effects of radiation pressure and Poynting Robertson light drag on the classical equilibrium points are analyzed by [7] and [8] . [9] has systematically discussed the dynamical effect of general drag in the planar circular restricted three body problem and has found that L4 and L5 are asymptotically stable with this kind of dissipation. It has been shown by [10] , [11] , [12] and [13] that, in the case of Stokes drags, exterior resonances may compensate the decrease of the semi major axis and that stationary solutions still exist. A numerical analysis of 1:1 resonance, taking into account the effect of the inclination and the eccentricity, has been studied by [14] . An analytical study of the linearised stability of L4 and L5 is provided in [4] .
Furthermore, [15] has examined the linear stability of triangular equilibrium points in the generalized photo gravitational restricted three body problem with Poynting Robertson drag. They have considered the smaller primary as an oblate body and bigger one as radiating and they have concluded that the triangular equilibrium points are unstable in linear sense. [16] has discussed the nonlinear stability in the generalized restricted three body problem with Poynting Robertson drag considering smaller primary as an oblate body and bigger one radiating. They have proved that the triangular points are stable in nonlinear sense. [17] has discussed the stability of triangular equilibrium points in photo gravitational circular restricted three body problem with Poynting Robertson drag and a smaller triaxial primary. They proved that the parameters involved in the problem (radiation pressure, oblateness and Poynting Robertson drag) influenced the position and linear stability of triangular points. In the presence of Poynting Robertson drag, triangular points are unstable, and in the absence of Poynting Robertson drag, these points are conditionally stable. In a series of papers, [18] has performed an analysis in the restricted three body problem with Poynting Robertson drag effect. They found that there existed two noncollinear stationary solutions which were linearly unstable.
In the present paper, we study the same problem but with the effects of stokes drag instead Poynting Robertson drag on noncollinear libration points L4 and L5 in the restricted three body problem.
2. Equations of Motion
Suppose  and
and  are the primaries revolving with angular velocity n in circular orbits about their centre of mass O, an infinitesimal mass
are the primaries revolving with angular velocity n in circular orbits about their centre of mass O, an infinitesimal mass  is moving in the plane of motion of
is moving in the plane of motion of 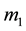 and
and . The line joining
. The line joining  and
and  is taken as X-axis and “O” their center of mass as origin and the line passing through O and perpendicular to OX and lying in the plane of motion of
is taken as X-axis and “O” their center of mass as origin and the line passing through O and perpendicular to OX and lying in the plane of motion of 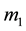 and
and ![]() is the Y-axis. We consider a synodic system of coordinates O (xyz); initially coincident with the inertial system O (XYZ), rotating with the angular velocity n about Z-axis; (the z-axis is coincident with Z-axis) (Figure 1).
is the Y-axis. We consider a synodic system of coordinates O (xyz); initially coincident with the inertial system O (XYZ), rotating with the angular velocity n about Z-axis; (the z-axis is coincident with Z-axis) (Figure 1).
In the synodic axes the equation of motion of ![]() in the restricted three body problem with Stokes drag S is
in the restricted three body problem with Stokes drag S is
![]() (1)
(1)
where
![]()
![]()
Figure 1. Configuration of the restricted three body problem with Stokes drag S.
![]() = Gravitational Force acting on
= Gravitational Force acting on ![]() due to
due to ![]()
![]() = Gravitational Force acting on
= Gravitational Force acting on ![]() due to
due to ![]()
![]() = Stokes drags Force acting on
= Stokes drags Force acting on ![]() due to
due to ![]() along
along![]() .
.
Its components along the synodic axes (x, y) are ![]() and
and ![]()
where
![]()
![]()
![]() Angular velocity of the axes
Angular velocity of the axes ![]() = const.
= const.
The equations of motion of ![]() in Cartesian coordinates (x, y) are
in Cartesian coordinates (x, y) are
![]()
![]() ,
,
where
n = Mean motion, G = Gravitational constant,
![]() and
and ![]() = coordinates of A and B in the synodic system.
= coordinates of A and B in the synodic system.
Using [2] terminology, the distance between primaries is unchanged and same is taken equal to one; the sum of the masses of the primaries is also taken as one. The unit of time is chosen so as to make the gravitational constant unity. The equations of motion of the infinitesimal mass ![]() in the synodic coordinate system (x, y) and dimensionless variables are
in the synodic coordinate system (x, y) and dimensionless variables are
![]() (2)
(2)
![]() (3)
(3)
where
![]()
![]() (4)
(4)
![]() (5)
(5)
![]()
The Stokes drag effect is of the order of ![]() (generally
(generally ![]() and
and ![]() as stated in the introduction).
as stated in the introduction).
3. Stationary Solutions (Libration Points)
The solutions (x, y) of Equations (2) and (3) with ![]() are given by
are given by
![]() (6)
(6)
and
![]() . (7)
. (7)
Here, if we take![]() , then it will be the classical case of the restricted three body problem and the solutions of these equations are just the five classical Lagrangian equilibrium points Li (i = 1, 2, 3, 4, 5). The Li (i = 1, 2, 3) are three collinear libration points which lie along the x-axis and Li (i = 4, 5) are the two non collinear libration points which make the equilateral triangles with the primaries. Due to the presence of the Stokes drag force, it is clear from Equations (6) and (7) that collinear equilibrium solution does not exist. Since there is a possibility of non collinear libration points under the effect of drag forces, so we restrict our analysis to these points. Their locations when
, then it will be the classical case of the restricted three body problem and the solutions of these equations are just the five classical Lagrangian equilibrium points Li (i = 1, 2, 3, 4, 5). The Li (i = 1, 2, 3) are three collinear libration points which lie along the x-axis and Li (i = 4, 5) are the two non collinear libration points which make the equilateral triangles with the primaries. Due to the presence of the Stokes drag force, it is clear from Equations (6) and (7) that collinear equilibrium solution does not exist. Since there is a possibility of non collinear libration points under the effect of drag forces, so we restrict our analysis to these points. Their locations when![]() , are (see, e.g., [19] )
, are (see, e.g., [19] )
![]() .
.
Now, we suppose that the solution of Equations (6) and (7) when ![]() and
and ![]() are given by
are given by
![]()
Making the above substitutions in Equations (6) and (7), and applying Taylors series expansion around the libration points by using that ![]() is a solution of these equations when
is a solution of these equations when![]() , we can get a linear set of equations.
, we can get a linear set of equations.
![]() (8)
(8)
and
![]() (9)
(9)
After substituting the values of the constants ![]() and
and ![]() in the above equations and rejecting the second and higher order terms in
in the above equations and rejecting the second and higher order terms in ![]() and
and![]() , we get the values of
, we get the values of ![]() and
and ![]() as
as
![]()
![]()
Hence, putting the values of ![]() and
and![]() , the displaced equilibrium points are given by
, the displaced equilibrium points are given by
![]() (10)
(10)
Here, the shifts in L4 and L5 are of![]() . If we calculate
. If we calculate ![]() numerically, taking
numerically, taking ![]() for different values of
for different values of![]() , we find that while using Stokes drag, as far as the values of
, we find that while using Stokes drag, as far as the values of ![]() increase corresponding
increase corresponding ![]() values decrease and the
values decrease and the ![]() values increase.
values increase.
4. Stability of L4, 5
We write the variational equations by putting ![]() and
and![]() ,
, ![]() ,
, ![]() , in the equations of motion (2) and (3), where
, in the equations of motion (2) and (3), where ![]() are the coordinates of the libration point. Therefore, expanding
are the coordinates of the libration point. Therefore, expanding ![]() and
and![]() by Taylors Theorem, we get
by Taylors Theorem, we get
![]() (11)
(11)
![]() (12)
(12)
Let us consider the trial solution of Equations (11) and (12),
![]()
where ![]() and
and ![]() are constants and
are constants and ![]() is a complex constant. Then we have
is a complex constant. Then we have
![]() (13)
(13)
![]() (14)
(14)
Now, from Equations (13) and (14), we derive the following simultaneous linear equations
![]() (15)
(15)
and
![]() (16)
(16)
The simultaneous linear Equations (15) and (16) can be written as
![]() (17)
(17)
![]() (18)
(18)
where
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
and
![]() (23)
(23)
Neglecting terms of![]() , the condition for the determinant of the linear equations defined by the Equations (17) and (18) to be zero is
, the condition for the determinant of the linear equations defined by the Equations (17) and (18) to be zero is
![]() (24)
(24)
This quadratic Equation (24) has the general form
![]() (25)
(25)
where
![]()
![]()
![]()
![]()
![]()
![]()
Here![]() ,
, ![]() and
and ![]() can be derived by evaluating e, f, g and h defined earlier. The value of the coefficient in the zero drag case is denoted by adding additional subscript 0. If we neglect product of powers of
can be derived by evaluating e, f, g and h defined earlier. The value of the coefficient in the zero drag case is denoted by adding additional subscript 0. If we neglect product of powers of ![]() with any of the constants defined in Equation (23), we obtain
with any of the constants defined in Equation (23), we obtain
![]() (26)
(26)
By assuming ![]() to be small, we investigate the stability of the non zero drag case. We can use the classical solutions of the zero drag case (i.e. when k = 0). Equation (25) reduces to
to be small, we investigate the stability of the non zero drag case. We can use the classical solutions of the zero drag case (i.e. when k = 0). Equation (25) reduces to
![]() (27)
(27)
The four classical solutions for L4 and L5 to ![]() are given by the pair of values
are given by the pair of values
![]() (28)
(28)
Since we are primarily interested in the stability of L4 and L5 under the effects of a drag force, we restrict our analysis to these points. The four roots of the classical characteristic equation can be written as
![]() (29)
(29)
where
![]() (30)
(30)
is a real quantity for L4 and L5. Using the values of ![]() and
and ![]() given in Equations (26) we have
given in Equations (26) we have
![]() (31)
(31)
With the introduction of drag we assume a solution of the form
![]() (32)
(32)
where ![]() and
and ![]() are small real quantities. To lowest order we have
are small real quantities. To lowest order we have
![]() (33)
(33)
![]() (34)
(34)
![]() (35)
(35)
Substituting these in Equation (25), and neglecting products of ![]() or
or ![]() with
with![]() , and solving the real and imaginary parts of the resulting simultaneous equations for
, and solving the real and imaginary parts of the resulting simultaneous equations for ![]() or
or ![]() we get
we get
![]() (36)
(36)
![]() (37)
(37)
(i) The stability of ![]()
For![]() , we have
, we have
![]() (38)
(38)
![]() (39)
(39)
On putting the values of![]() , in Equations (38) and (39) from Equation (26) and also taking,
, in Equations (38) and (39) from Equation (26) and also taking, ![]() , we have
, we have
![]()
Now, putting these values of ![]() and
and ![]() in Equation (35), and neglecting the terms of
in Equation (35), and neglecting the terms of![]() , we get the characteristic equation as
, we get the characteristic equation as
![]()
whose roots are
![]()
Also on taking ![]() in Equations (38) and (39) from Equation (26), we get the characteristic equation as
in Equations (38) and (39) from Equation (26), we get the characteristic equation as
![]()
whose roots are
![]()
If ![]()
According to [9] , the resulting motion of a particle is asymptotically stable only when all the real parts of ![]() are negative and the condition for asymptotically stable under the arbitrary drag force is given by
are negative and the condition for asymptotically stable under the arbitrary drag force is given by
![]() (40)
(40)
where ![]() and
and ![]() are defined in Equation (26). But we see that the linear stability of triangular equilibrium points does not depend on the value of
are defined in Equation (26). But we see that the linear stability of triangular equilibrium points does not depend on the value of ![]() and
and![]() . Therefore the condition
. Therefore the condition ![]() can only be satisfied when k is positive and the drag force is a function of
can only be satisfied when k is positive and the drag force is a function of ![]() and
and![]() .
.
But here in our case of Stokes drag ![]() and therefore
and therefore ![]() and hence L4 is not asymptotically stable. Further one of the roots of
and hence L4 is not asymptotically stable. Further one of the roots of ![]() i.e.
i.e. ![]() has positive real root. Therefore L4 is not stable. Thus we conclude that L4 is neither stable nor asymptotically stable and hence linearly unstable.
has positive real root. Therefore L4 is not stable. Thus we conclude that L4 is neither stable nor asymptotically stable and hence linearly unstable.
Similarly, we conclude that ![]() is neither stable nor asymptotically stable and hence linearly unstable.
is neither stable nor asymptotically stable and hence linearly unstable.
5. Conclusions
We have studied the existence of the triangular libration points and their linear stability by using Stokes drag. We have shown that there exist two noncollinear stationary points ![]() and
and ![]() (Equation (10)). If we put
(Equation (10)). If we put![]() , these results agree with the classical restricted three body problem.
, these results agree with the classical restricted three body problem.
In the classical case i.e. when![]() , we observe that as the value of
, we observe that as the value of ![]() increases, the abscissa
increases, the abscissa ![]() of
of ![]() decreases and the ordinate
decreases and the ordinate ![]() of
of ![]() remains constant, while in our case (i.e. Stokes drag), when
remains constant, while in our case (i.e. Stokes drag), when![]() , we observe that the abscissa
, we observe that the abscissa ![]() of
of ![]() decreases and the ordinate
decreases and the ordinate ![]() of
of ![]() changes slightly. In our previous paper ( [18] ) i.e. in the case of Poynting Robertson drag, the abscissa and the ordinate decrease with
changes slightly. In our previous paper ( [18] ) i.e. in the case of Poynting Robertson drag, the abscissa and the ordinate decrease with![]() . As regards, the stability of
. As regards, the stability of ![]() in both the cases (Poynting Robertson drag and Stokes drag) is always unstable for all values of
in both the cases (Poynting Robertson drag and Stokes drag) is always unstable for all values of![]() . The result of stability is quite different when we compare with the classical case. In the classical case,
. The result of stability is quite different when we compare with the classical case. In the classical case, ![]() is stable for
is stable for![]() , whereas in the case of drag forces, motion is unstable for all values of
, whereas in the case of drag forces, motion is unstable for all values of![]() .
.
In the case of Stokes drag, we have derived a set of linear equations in terms of ![]() and
and ![]() (Equations (17) and (18)), which involve the components of the Stokes drag force evaluated at the libration points (Equations (19)-(23)). From these, we derive a characteristic equation having the general form (Equation (25)).
(Equations (17) and (18)), which involve the components of the Stokes drag force evaluated at the libration points (Equations (19)-(23)). From these, we derive a characteristic equation having the general form (Equation (25)).
Further, we have derived the approximate expressions for ![]() and
and ![]() occurring in the above characteristic equation. These expressions are given in terms of the partial derivatives of the Stokes drag, evaluated at the libration points.
occurring in the above characteristic equation. These expressions are given in terms of the partial derivatives of the Stokes drag, evaluated at the libration points.
Using the [9] terminology, in the case of drag force, we assume a solution of the form (Equation (32)), where ![]() and
and ![]() are small real quantities and
are small real quantities and
![]()
is a real quantity for L4 and L5 in the classical case. After substituting the values of![]() ,
, ![]() ,
, ![]() and
and ![]() in the characteristic equation, we get the values of
in the characteristic equation, we get the values of ![]() and
and ![]() (Equations (36) and (37)).
(Equations (36) and (37)).
Further to investigate the stability of the shifted points, by using [9] terminology, the resulting motion of a particle is asymptotically stable only when all the real parts of ![]() are negative. Also, the condition for asymptotical stability under the drag force is given by Equation (40).
are negative. Also, the condition for asymptotical stability under the drag force is given by Equation (40).
The condition ![]() can only be satisfied when k > 0. In the case of Stokes drag
can only be satisfied when k > 0. In the case of Stokes drag ![]() and
and![]() , Equation (40) is not satisfied. Therefore, L4 and L5 are not asymptotically stable. Further, we have seen that one of the roots of
, Equation (40) is not satisfied. Therefore, L4 and L5 are not asymptotically stable. Further, we have seen that one of the roots of ![]() i.e.
i.e. ![]() has positive real root; thus, L4 and L5 are not stable. Hence, due to Stokes drag, L4 and L5 are neither stable nor asymptotically stable but unstable whereas in the classical case L4 and L5 are stable for the mass ratio
has positive real root; thus, L4 and L5 are not stable. Hence, due to Stokes drag, L4 and L5 are neither stable nor asymptotically stable but unstable whereas in the classical case L4 and L5 are stable for the mass ratio ![]() [19] .
[19] .