On the Computation of Extinction Time for Some Nonlinear Parabolic Equations ()
1. Introduction
There is a large number of nonlinear partial differential equations of parabolic type whose solutions for given initial data become identically nulle in finite time T. Such a phenomenon is called extinction and T is called the extinction time. For certain problems, the extinction time can be computed explicitly, but in many cases one can only know the existence of extinction time.
Since the appearance of the pioneering work of Kalashnikov [1] , extinction phenomenon in nonlinear parabolic equations has been studied extensively by many authors [2] [3] . Particular emphasis has been placed on the question as to the existence of extinction time [4] - [7] .
Generally speaking, it is difficult to simulate extinction phenomenon accurately on general domains. Indeed, it is not at all clear if features of such a phenomenon as extinction can be well reflected in the discretized equation which approximates the original equation. In [8] - [11] , some numerical schemes have been used to study the extinction phenomenon of solutions for some nonlinear parabolic equations.
In this work, we propose a numerical algorithm for computing the extinction time for nonnegative solutions of some nonlinear parabolic equations. Our motivation is to reproduce the extinction phenomenon of some non- linear parabolic equations on general domains.
This paper is organized as follows. In the next section, we present the problem model and some theoretical results. A discretization of this problem is derived in Section 3, while numerical experiments are reported in Section 4 and Section 5 is devoted to concluding remarks.
2. The Model Problem
In this work, we are concerned with the following initial-boundary value problem:
 , (1)
, (1)
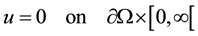 , (2)
, (2)
 , (3)
, (3)
where  is a
is a 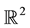 bounded domain with boundary
bounded domain with boundary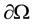 ,
,  ,
,  and
and , being given functions.
, being given functions.
Furthermore, for any  and for all
and for all 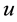 defined in
defined in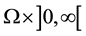 , we will set
, we will set ,
,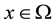 .
.
Nonlinear parabolic equations of type (1) appear in various applications. In particular they are used to des- cribe a phenomenon of thermal propagation in an absorptive medium where 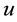 stands for temperature [5] . In other applications,
stands for temperature [5] . In other applications, 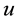 is a concentration and the process is described as diffusion with absorption.
is a concentration and the process is described as diffusion with absorption.
The problem of determining necessary and sufficient conditions on the functions ![]() and
and ![]() which ensure the existence of an extinction time for solutions of (1)-(3) has been considered by several authors [1] [6] [7] [12] .
which ensure the existence of an extinction time for solutions of (1)-(3) has been considered by several authors [1] [6] [7] [12] .
In this section, we state the following result:
Theorem 1 Assume that ![]() is a nonnegative solution of the problem (1)-(3) where f and F are nondecreasing, nonnegative derivatives functions and if
is a nonnegative solution of the problem (1)-(3) where f and F are nondecreasing, nonnegative derivatives functions and if![]() , then
, then
![]()
Proof: First, let us set![]() . We have
. We have
![]() . (i)
. (i)
Multiplying Equation (1) by ![]() and integrating over
and integrating over ![]() it follows
it follows
![]() . (ii)
. (ii)
On one hand thanks to regularity of functions![]() ,
, ![]() and
and![]() , we can write
, we can write
![]()
where ![]() is the unit outward to
is the unit outward to![]() , ds denotes an element of surface area, since
, ds denotes an element of surface area, since ![]() vanishes on
vanishes on ![]() and
and
![]() , we have
, we have![]() , hence
, hence
![]() . (iii)
. (iii)
From (ii) and (iii), we deduce
![]()
Since ![]() and
and![]() , and according to (i), we obtain
, and according to (i), we obtain
![]() . (iv)
. (iv)
On the other hand, multiplying Equation (1) by ![]() yields
yields
![]() ,
,
which we rewrite as
![]() ,
,
then the application ![]() is decreased in
is decreased in![]() . It then follows
. It then follows
![]() . (vi)
. (vi)
On the other hand, the increase of ![]() implies that
implies that
![]() ,
,
Thus
![]()
and according to (vi) we obtain
![]() ,
,
This last inequality implies
![]() .
.
Then considering (iv), we deduced
![]() . (vii)
. (vii)
Setting![]() , we obtain
, we obtain
![]() .
.
This gives after integrating
![]() .
.
Knowing that![]() . it follows
. it follows![]() . The passage to the limit allows us to write
. The passage to the limit allows us to write
![]() .
.
Finally,
![]() .
.
In addition to the assumption of increase of F in Theorem 2.1, if we assume that
![]() , (4)
, (4)
![]() is a positive constant.
is a positive constant.
then the following result is easily shown.
Corollary 1 Suppose that the assumptions of the Theorem 2.1 are satisfied, and if (4) holds for![]() , then
, then
![]() . (5)
. (5)
Indeed, for all ![]() solution of (1)-(3), it comes from the assumption (4) that
solution of (1)-(3), it comes from the assumption (4) that
![]() ,
,
that gives
![]() .
.
As![]() , then
, then
![]() .
.
So
![]() ,
,
and as a consequence of Theorem 2.1
![]() . □
. □
In summary, under some assumptions we know that all nonnegative solutions of (1)-(3) have extinction time as![]() . We want to determine whether extinction occurs in finite time for any given
. We want to determine whether extinction occurs in finite time for any given ![]() and
and![]() .
.
It is well known that, in general, there is no classical solution to this nonlinear parabolic equation for arbitrary choices of ![]() and
and![]() . However, there are some works dealing with approximation of extinction time for solutions of (1). For example, in [13] a numerical method to approximate the solutions of (1) has been developed in the case
. However, there are some works dealing with approximation of extinction time for solutions of (1). For example, in [13] a numerical method to approximate the solutions of (1) has been developed in the case ![]() and in [14] an algorithm based on splitting technique was derived to compute the extinction time for solutions on a rectangular domain.
and in [14] an algorithm based on splitting technique was derived to compute the extinction time for solutions on a rectangular domain.
In order to determine the extinction time for some ![]() and
and![]() , we will derive in the next section a numerical scheme based on Donor-cell scheme. Given a sufficiently small parameter
, we will derive in the next section a numerical scheme based on Donor-cell scheme. Given a sufficiently small parameter![]() , we would like to determine the positive real
, we would like to determine the positive real ![]() such that a solution
such that a solution ![]() of the problem (1)-(3) has to satisfy the above relation
of the problem (1)-(3) has to satisfy the above relation
![]() . (6)
. (6)
We shall call ![]() satisfying (6) as the
satisfying (6) as the ![]() -extinction time.
-extinction time.
3. Discretization
3.1. Discretization of the Studied Domain
Let ![]() be a considered domain that we assume to be of irregular shape, we approximate
be a considered domain that we assume to be of irregular shape, we approximate ![]() by a domain
by a domain ![]() whose boundary is specified by the set of boundary edges lying on gridlines. We imbed
whose boundary is specified by the set of boundary edges lying on gridlines. We imbed ![]() in a rectan- gular domain
in a rectan- gular domain![]() ,
, ![]() of smallest possible size. Given two nonzero integers
of smallest possible size. Given two nonzero integers ![]() and
and
![]() , we set
, we set ![]()
![]() and we introduce on
and we introduce on ![]() a grid of step
a grid of step ![]() and
and ![]() in x
in x
and ![]() direction respectively. The set of points
direction respectively. The set of points ![]() such that of
such that of![]() ,
, ![]() defines the discretization of
defines the discretization of ![]() into
into ![]() cells (rectangular subdomains). For all
cells (rectangular subdomains). For all![]() ,
, ![]() cell
cell
![]() occupies the spatial region
occupies the spatial region ![]() and has center the point noted
and has center the point noted![]() .
.
The cells of ![]() are then divided into inner cell (which lie completely in
are then divided into inner cell (which lie completely in![]() ), external cell (which lie in
), external cell (which lie in![]() ) and boundary cells (which lie in a part of
) and boundary cells (which lie in a part of![]() ). The problem model is then solved only in the inner cells.
). The problem model is then solved only in the inner cells.
A matrix of size ![]() gives a description of the discretized domain. For example, consider three sets of indices
gives a description of the discretized domain. For example, consider three sets of indices![]() ,
, ![]() et
et ![]() corresponding to the inner, boundary and external cells, we then admit to define the following matrix
corresponding to the inner, boundary and external cells, we then admit to define the following matrix
![]() (7)
(7)
the matrix to identify cell types.
The idea of this numerical treatment of general domains has been suggested by Griebel et al. in [15] . An example of this numerical treatment is illustrated in Figure 1 and its matrix representative is given by the following (8).
![]() (8)
(8)
3.2. Spatial Discretization
First of all, let us give an approximation of the diffusion operator at the point ![]() which we rewrite as
which we rewrite as
![]() (9)
(9)
![]()
Figure 1. An example of the discretization of a non rectangular domain into cells.
Let ![]() be the approximation of
be the approximation of ![]() at the cell center
at the cell center![]() . In the following we do apply a discretization that is similar to the one of Donor-cell scheme where the expression
. In the following we do apply a discretization that is similar to the one of Donor-cell scheme where the expression ![]() is approached by a progressive finite differences scheme and
is approached by a progressive finite differences scheme and ![]() by a central finite differences scheme.
by a central finite differences scheme.
Furthermore, we set ![]() where
where ![]() and we note
and we note
![]() (10)
(10)
If ![]() denotes the vector of components
denotes the vector of components ![]() then, one can write
then, one can write
![]() (11)
(11)
where ![]() the diagonal matrix whose diagonal is the vector
the diagonal matrix whose diagonal is the vector ![]() and
and ![]() denotes forward differentiation matrix the
denotes forward differentiation matrix the ![]() -direction.
-direction.
On the other hand, denoting by ![]() the approached value of
the approached value of ![]() at the cell center
at the cell center ![]() and
and
noting by
![]()
the vector of the value of ![]() at point
at point![]() , it follows through the central difference scheme, the relation
, it follows through the central difference scheme, the relation
![]() (12)
(12)
which is written by the mean of the Equation (12) as
![]() , (13)
, (13)
where ![]() denotes central differentiation matrix in the
denotes central differentiation matrix in the ![]() -direction.
-direction.
Similarly, given![]() , the vector of the approached values of
, the vector of the approached values of ![]() at point
at point![]() , we obtain
, we obtain
![]() , (14)
, (14)
where ![]() denotes forward differentiation matrix in the
denotes forward differentiation matrix in the ![]() -direction.
-direction.
From Equations (13) and (14), we deduce the approximation of the operator ![]() at cell center
at cell center![]() , in matrix form:
, in matrix form:
![]() (15)
(15)
where ![]() is the vector of value of
is the vector of value of ![]() at points
at points![]() . Thus, we have defined, an approximation operator
. Thus, we have defined, an approximation operator ![]() to approach the operator
to approach the operator![]() .
.
However, it should be noted that ![]() is a vector dependent of
is a vector dependent of![]() .
.
Considering lexicographic numerotation, we note by ![]() the vector of the values of u in points
the vector of the values of u in points ![]() at time t. Knowing that
at time t. Knowing that ![]() at points
at points![]() , and the differentiation matrices
, and the differentiation matrices ![]() to approach the derivative on the set of the points
to approach the derivative on the set of the points ![]() we can replace respectively by the matrices which are obtained by deleting the rows and columns corresponding to the indices of the points
we can replace respectively by the matrices which are obtained by deleting the rows and columns corresponding to the indices of the points ![]() of
of![]() .
.
Given the Equation (15), the discrete system approaching the problem (1)-(3) is rewritten by
![]() , (16)
, (16)
where we have set
![]()
and where ![]() is the matrix obtained of
is the matrix obtained of ![]() by deleting the rows and columns corresponding to
by deleting the rows and columns corresponding to
the indices of the points ![]() of
of ![]() and
and ![]() is the vector of values of
is the vector of values of![]() ,
,![]() .
.
Furthermore, the initial condition is written
![]() (17)
(17)
where ![]() is the vector obtained from
is the vector obtained from ![]() by deleting the elements corresponding to the indices of the points
by deleting the elements corresponding to the indices of the points ![]() of
of ![]()
3.3. Temporal Discretization
For a time step fixed![]() , we consider the sequence
, we consider the sequence ![]() defined by
defined by ![]() et
et![]() . Then, we
. Then, we
denote ![]() the approximation at time
the approximation at time ![]() of vector
of vector ![]() solution of (16)-(17). Using the explicit Euler method, the semi-discret scheme is written
solution of (16)-(17). Using the explicit Euler method, the semi-discret scheme is written
![]() (18)
(18)
where we set![]() .
.
It should be noticed that if the time step ![]() is chosen to be little enough, and F satisfied the growth con- dition (4),
is chosen to be little enough, and F satisfied the growth con- dition (4),
![]() (19)
(19)
Thus the extinction time is obtained using simple itrations process until the stopping criterion
![]() (20)
(20)
is satisfied. Here ![]() is the given tolerance number. The sequence of computations to be performed is sum- marized as follows
is the given tolerance number. The sequence of computations to be performed is sum- marized as follows
Algorithm 3.1
1. Read ![]() and
and![]() .
.
2. Compute ![]() and
and![]() .
.
3. Define ![]() (rectangular) and
(rectangular) and ![]() (non rectangular) such
(non rectangular) such![]() .
.
4. Compute the matrix ![]() and
and![]() .
.
5. Set![]() .
.
6. Assign initial value to![]() .
.
7. Set![]() .
.
8. While ![]() and
and![]() , do.
, do.
9. Compute ![]() according to (18) .
according to (18) .
10. Set![]() .
.
11.![]() .
.
End while
4. Numerical Experiments
Let ![]() be a bounded domain in
be a bounded domain in![]() . Consider the initial value problem
. Consider the initial value problem
![]() (21)
(21)
![]() (22)
(22)
![]() . (23)
. (23)
where ![]() is the continuous nonnegative function in
is the continuous nonnegative function in![]() , vanishing on
, vanishing on![]() , and
, and![]() .
.
Equation (21) models heat propagation in medium where the solution ![]() stands for temperature.
stands for temperature.
For our numerical experiments we have consider Figure 2 to be our studied domain and we have use discretization parameters![]() , and
, and![]() .
.
We would like to numerically estimate the extinction time for solutions of problem (21)-(23) with the initial condition given by
![]()
First, for fixed accurate value![]() , we estimate the
, we estimate the ![]() -euclidian norm of the sequence
-euclidian norm of the sequence ![]() solution of the numerical scheme (18) for various values of parameters
solution of the numerical scheme (18) for various values of parameters![]() . Table 1 and Figure 3 clearly show that the approximation extinction time can be given by
. Table 1 and Figure 3 clearly show that the approximation extinction time can be given by
![]() (24)
(24)
We can see in Table 1 that this value is approximated by
![]() (25)
(25)
Also, the extinction process is illustrated by Figure 4 where we can appreciate the numerical solution extinct in a finite time.
5. Concluding Remarks
In this paper, a numerical algorithm based on Donor-cell scheme was proposed in order to compute the extinc- tion time for nonnegative solutions of some nonlinear parabolic equations on general domains. We have verified
![]()
Figure 2. Discretization of studied domain ![]() into cells.
into cells.
![]()
Table 1. Numerical extinction time relatively to time iteration parameter n.
![]()
Figure 3. Variation norm of the numerical solution.
![]()
Figure 4. Extinction phenomenon of the numerical solution.
experimentally for a class of nonlinear parabolic equations that the numerical algorithm is efficient for comput- ing the extinction time of solutions.
In the works to come, it will be better to apply the numerical algorithm to study, for example, moving boun- dary problems and extinction problems in environment.
Acknowledgements
We thank the Editor and the referee for their comments.