The Initial Boundary Value Problem for Modified Zakharov System ()
1. Introduction
In this paper, we study the global existence and uniqueness of solutions for a modified Zakharov system with initial boundary value conditions as follows.
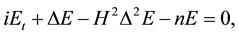 (1.1)
(1.1)
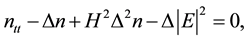 (1.2)
(1.2)
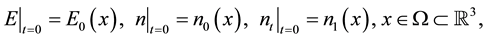 (1.3)
(1.3)
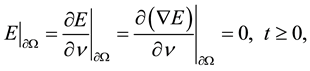 (1.4)
(1.4)
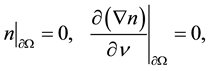 (1.5)
(1.5)
where 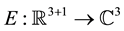 represents the slowly varying envelope of the electric field,
represents the slowly varying envelope of the electric field, 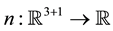 denotes deviation of the ion density from its mean, and H is the dimensionless quantum parameter given by the ratio of the ion plasmon and electron thermal energies.
denotes deviation of the ion density from its mean, and H is the dimensionless quantum parameter given by the ratio of the ion plasmon and electron thermal energies.
The classical Zakharov system was derived by Zakharov to describe the propagation of Langmuir waves in a plasma [1] . In the past decade, a large amount of work has been devoted to the existence problem for the classical Zakharov system. For instance, the Fourier restriction norm method, applies to this problem, and under appropriate assumption on the data, several existence results have been established. The local well-posedness of this problem on 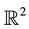 in the energy space
in the energy space 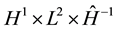 was first obtained by Bourgain and Colliander [2] , which was improved to
was first obtained by Bourgain and Colliander [2] , which was improved to 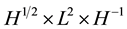 by Ginibre, Tsutsumi and Velo [3] . Recently, Bejenaru, Herr, Holmer and Tataru have obtained local well-posedness in
by Ginibre, Tsutsumi and Velo [3] . Recently, Bejenaru, Herr, Holmer and Tataru have obtained local well-posedness in 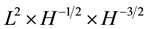 [4] . Another approach was initiated by Colliander, Keel, Stafflani, Takaoka, and Tao in [5] , called the I-method. This method was successfully applied by these authors to the Kdv and modified Kdv equation. In [6] , this method was also used to construct global solutions for the one dimensional Zakharov system.
[4] . Another approach was initiated by Colliander, Keel, Stafflani, Takaoka, and Tao in [5] , called the I-method. This method was successfully applied by these authors to the Kdv and modified Kdv equation. In [6] , this method was also used to construct global solutions for the one dimensional Zakharov system.
However, some important effects, such as quantum effects, have been ignored in the classical Zakharov system. The importance of quantum effects in ultrasmall electronic devices, dense astrophysical plasma systems and laser plasmas has produced an increasing interest on the investigation of the quantum counterpart of some of plasma physics phenomena [7] . By using a quantum fluid approach, Garcia has obtained the following modified Zakharov system [8] :
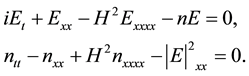
Recently, S. You and B. Guo have considered the existence and uniqueness of the global solution to the initial boundary value problem for the above system in 1 dimension and 2 dimensions, respectively [9] [10] . Motivated by their result, we consider the global existence of solutions in 3 dimensions with small initial condition. As is standard, the problem is to obtain a prior estimate of higher derivatives of solutions in some suitable function spaces. To overcome higher dimensional difficulty, we use continuity lemma and the linear interpolation theory, together with the properties of Sobolev spaces to handle it.
Now we give some notations:
-For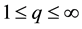 , we denote by
, we denote by 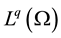 or simply
or simply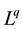 , the space of all q times integrable functions in
, the space of all q times integrable functions in 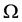 equipped with norm
equipped with norm ![]() or simply
or simply![]() .
.
![]()
-Let ![]() be the usual Sobolev space of complex-valued functions with the norm
be the usual Sobolev space of complex-valued functions with the norm
![]()
-We denote by C a positive constant which may change from one line to the next line.
2. A Prior Estimates
To study the smooth solution of the modified Zakharov system, we introduce function![]() , and transform Equations (1.1)-(1.5) into the form:
, and transform Equations (1.1)-(1.5) into the form:
![]() (2.1)
(2.1)
![]() (2.2)
(2.2)
![]() (2.3)
(2.3)
with initial condition
![]() (2.4)
(2.4)
and boundary condition
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
Lemma 2.1. Assume that![]() , and
, and ![]() is the solution to (2.1)-(2.6), then we have
is the solution to (2.1)-(2.6), then we have
![]()
Proof. Multiplying Equation (2.1) by![]() , and integrating over
, and integrating over![]() , we have
, we have
![]() (2.7)
(2.7)
Since
![]()
![]()
Taking the imaginary part of Equation (2.7), then we have
![]()
Lemma 2.2. [11] (Continuity lemma) Assume that ![]() is a nonnegative continuous function defined on
is a nonnegative continuous function defined on ![]() and
and
![]()
If ![]() and
and ![]() also hold, then
also hold, then ![]() is bounded in
is bounded in![]() .
.
Lemma 2.3. [11] (Gargliardo-Nirenberg inequality) Assume that ![]()
![]()
![]()
![]()
![]() then
then
![]()
where ![]()
Lemma 2.4. Assume that ![]() is the solution to (2.1)-(2.6), and
is the solution to (2.1)-(2.6), and ![]() then we have
then we have
![]()
Proof. Multiplying Equation (2.1) by![]() , and integrating over
, and integrating over![]() , we have
, we have
![]() (2.8)
(2.8)
Since
![]()
then taking the real part of Equation (2.8), we have
![]() (2.9)
(2.9)
where we have used the fact
![]()
Similarly, multiplying Equation (2.2) by![]() , and integrating over
, and integrating over![]() , we have
, we have
![]() (2.10)
(2.10)
i.e.
![]() (2.11)
(2.11)
Adding Equation (2.9) to Equation (2.11), we deduce
![]()
Set ![]() then we have
then we have
![]()
therefore, using Young’s inequality, we have
![]() (2.12)
(2.12)
Choosing ![]() such that
such that![]() , and by Lemma 2.3, we have
, and by Lemma 2.3, we have
![]()
Set ![]() then the above inequality can be simplified as
then the above inequality can be simplified as ![]() where
where
![]() then using Lemma 2.2 yields
then using Lemma 2.2 yields
![]()
if the initial condition is small enough. Substituting it into Equation (2.12), we have
![]()
Lemma 2.5. Assume that ![]() is the solution to (2.1)-(2.6), and
is the solution to (2.1)-(2.6), and ![]() we have
we have
![]()
Proof. Differentiating Equation (2.1) with respect to t, and then multiplying it by![]() , integrating over
, integrating over![]() , we have
, we have
![]() (2.13)
(2.13)
Since
![]()
Taking the imaginary part of Equation (2.13) yields
![]()
therefore, using Hölder’s inequality and Sobolev imbedding, we have
![]() (2.14)
(2.14)
Differentiating Equation (2.2) with respect to t, and then multiplying it by![]() , integrating over
, integrating over![]() , we have
, we have
![]()
i.e.
![]()
therefore
![]() (2.15)
(2.15)
Adding Equation (2.14) to Equation (2.15), we have
![]()
Using Gronwall’s inequality, we have
![]()
From Equation (2.1), Equation (2.2), and Equation (2.3), it easily get
![]()
3. Existence and Uniqueness of Global Solution
Theorem 3.1. Assume that ![]() then there exists a unique global solution of the initial boundary value problem (2.1)-(2.6),
then there exists a unique global solution of the initial boundary value problem (2.1)-(2.6),
![]()
![]()
![]()
Proof. We first give the proof of the uniqueness of the solution. Suppose ![]() and
and ![]() are two solutions of (2.1)-(2.6). Let
are two solutions of (2.1)-(2.6). Let
![]()
therefore
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
![]() (3.3)
(3.3)
with initial condition
![]() (3.4)
(3.4)
Multiplying Equation (3.1) by![]() , and integrating over
, and integrating over![]() , we have
, we have
![]()
taking the imaginary part yields
![]()
therefore
![]() (3.5)
(3.5)
Multiplying Equation (3.3) by![]() , and integrating over
, and integrating over![]() , we have
, we have
![]()
Since
![]()
![]()
![]()
therefore
![]() (3.6)
(3.6)
Adding Equation (3.5) to Equation (3.6), we have
![]()
Using Gronwall’s inequality and the initial condition Equation (3.4), we can obtain
![]()
Next we show the existence of the solution.
By using the Garlerkin method, choose basic functions ![]() such that
such that![]() , where
, where ![]() are different corresponding eigenvalues. The approximate solution of problem (2.1)- (2.6) can be written as
are different corresponding eigenvalues. The approximate solution of problem (2.1)- (2.6) can be written as
![]()
![]()
![]()
where the undetermined coefficients ![]() need to satisfy the following initial value problem of the system of ordinary differential equations
need to satisfy the following initial value problem of the system of ordinary differential equations
![]()
![]()
![]()
with initial conditions
![]()
![]()
![]()
According to the basic theory of ordinary differential equations, the above equations have a unique local solution.
Similarly to the proof of Lemma 2.1 and Lemma 2.4, we have
![]()
By compactness argument, we can choose subsequences, still denoted by ![]() such that
such that
![]() in
in ![]() weakly star;
weakly star;
![]() in
in ![]() weakly star;
weakly star;
![]() in
in ![]() weakly star;
weakly star;
![]() in
in ![]() weakly star;
weakly star;
![]() in
in ![]() strongly and a.e.;
strongly and a.e.;
![]() in
in ![]() strongly and a.e.;
strongly and a.e.;
![]() in
in ![]() weakly star;
weakly star;
![]() in
in ![]() weakly star.
weakly star.
Indeed
![]()
![]()
By using the density of ![]() in
in![]() , we get the existence of a local generalized solution for the problem (2.1)-(2.6). By continuous extension principle and a prior estimate in Section 2, we can get the existence of the global solution.
, we get the existence of a local generalized solution for the problem (2.1)-(2.6). By continuous extension principle and a prior estimate in Section 2, we can get the existence of the global solution.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 11271141, No. 11426069 and No.61375006).
NOTES
*Corresponding author.