New Oscillation Criteria of Second-Order Nonlinear Delay Dynamic Equations on Time Scales ()
1. Introduction
According to the important academic value and application background in Quantum Physics (especially in Nuclear Physics), engineering mechanics and control theory, the oscillation theory of dynamic equations on time scales has become one of the research hotspots. The paper will deal with the oscillatory behavior of all solutions of second-order nonlinear delay dynamic equation
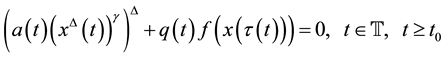 (1)
(1)
In order to obtain the main results, we give the following hypotheses:
(H1) 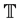 is a time scale (i.e., a nonempty closed subset of the real numbers
is a time scale (i.e., a nonempty closed subset of the real numbers ) which is unbounded above, and
) which is unbounded above, and  with
with . We define the time scale interval of the form
. We define the time scale interval of the form 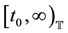 by
by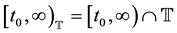 .
.
(H2)  is the ratio of two positive odd integers.
is the ratio of two positive odd integers.
(H3) a, q are positive real-valued right-dense continuous functions on an arbitrary time scale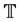 .
.
(H4) 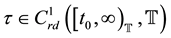 is a strictly increasing function such that
is a strictly increasing function such that  and
and 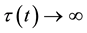 as
as 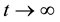 and
and .
.
(H5) 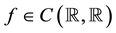 is a continuous function, for some positive constant L which satisfies
is a continuous function, for some positive constant L which satisfies
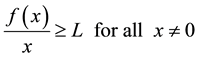
According to the solution of (1), we mean a nontrivial real-valued function x satisfying (1) for![]() . We recall that a solution x of Equation (1) is said to be oscillatory on
. We recall that a solution x of Equation (1) is said to be oscillatory on ![]() in case it is neither eventually positive nor eventually negative; otherwise, the solution is said to be nonoscillatory. Equation (1) is said to be oscillatory in case all of its solutions are oscillatory. Our attention is restricted on those solutions of (1) which are not eventually identically zero. Since
in case it is neither eventually positive nor eventually negative; otherwise, the solution is said to be nonoscillatory. Equation (1) is said to be oscillatory in case all of its solutions are oscillatory. Our attention is restricted on those solutions of (1) which are not eventually identically zero. Since![]() , we shall consider both the cases
, we shall consider both the cases
![]() (2)
(2)
and
![]() (3)
(3)
It is easy to see that (1) can be transformed into a second-order nonlinear delay dynamic equation
![]() (4)
(4)
where![]() . In (1), if
. In (1), if![]() ,
, ![]() , then (1) is simplified to an equation
, then (1) is simplified to an equation
![]() (5)
(5)
In (4), if![]() , then (4) is simplified to an equation
, then (4) is simplified to an equation
![]() (6)
(6)
In (6), if![]() , then (6) is simplified to an equation
, then (6) is simplified to an equation
![]() (7)
(7)
After the careful consideration of the linear delay dynamic equations by Agarwal, Bohner and Saker in 2005 [1] (7) and the nonlinear delay dynamic equations by Sahiner [2] (6), some sufficient conditions for oscillation of (7) and (6) have been established. In 2007, Erbe, Peterson and Saker [3] considered the general nonlinear delay dynamic equations (4) and obtained some new oscillation criteria, which improved the results given by Sahiner [2] . Saker [4] in 2005 and Grace, Bohner and Agarwal [5] in 2009 considered the half-linear dynamic equations (5), and established some sufficient conditions for oscillation of (5). For other related results, we recommend the references [6] -[10] . On the basis of these, by using the generalized Riccati transformation and integral averaging technique, we continue to discuss the oscillation of solutions of (1) and obtain some new oscillatory criteria of Philos-type for (1).
A time scale ![]() is an arbitrary nonempty closed subset of the real numbers
is an arbitrary nonempty closed subset of the real numbers![]() . Since we are interested in oscillatory behavior, we suppose that the time scale under consideration is not bounded above, i.e., sup
. Since we are interested in oscillatory behavior, we suppose that the time scale under consideration is not bounded above, i.e., sup![]() . On any time scale we define the forward and the backward jump operators by
. On any time scale we define the forward and the backward jump operators by
![]()
A point ![]() is said to be left-dense if
is said to be left-dense if![]() , right-dense if
, right-dense if![]() , left-scattered if
, left-scattered if ![]() and right-scattered if
and right-scattered if![]() . The graininess
. The graininess ![]() of the time scale is defined by
of the time scale is defined by![]() . A function
. A function ![]() is said to be rd-continuous if it is continuous at each right-dense point and if there exists a finite left limit at all left-dense points.
is said to be rd-continuous if it is continuous at each right-dense point and if there exists a finite left limit at all left-dense points.
Throughout this paper, we will make use of the following product and quotient rules for the derivative of the product fg and the quotient ![]() of two differentiable functions f and g
of two differentiable functions f and g
![]() (8)
(8)
![]() (9)
(9)
For ![]() and a differentiable function f, the Cauchy integral of
and a differentiable function f, the Cauchy integral of ![]() is defined by
is defined by
![]()
The integration by parts formula reads
![]() (10)
(10)
and infinite integrals are defined by
![]()
For more details, see [11] [12] .
2. Main Results
In order to obtain the main results, the following lemmas are first introduced.
Lemma 1 (Han et al. [[10] , Lemma 2.2]) Assume that ![]() is strictly increasing and
is strictly increasing and ![]() is a time scale,
is a time scale,![]() . Let
. Let![]() . If
. If![]() , and let
, and let ![]() exist for
exist for![]() , then
, then ![]() exist, and
exist, and
![]() (11)
(11)
Lemma 2 (Bohner et al. [[11] , Theorem 1.90]) Assume that ![]() is Δ-differentiable and eventually positive or eventually negative, then
is Δ-differentiable and eventually positive or eventually negative, then
![]() (12)
(12)
Lemma 3 (Sun et al. [[13] , Lemma 2.1]) Assume that the conditions (H1)-(H5) and (2) hold, and let ![]() be an eventually position solution of (1), then there exists
be an eventually position solution of (1), then there exists ![]() such that
such that
![]() (13)
(13)
Next, we will provide a new sufficient condition for oscillation of all solutions of (1), which can be considered as the extension of the result of Philos [14] for oscillation of second-order differential equations.
Theorem 1 Assume that the conditions (H1) - (H5), (2) hold and![]() . Let
. Let ![]() be a rd-continuous function such that
be a rd-continuous function such that
![]()
and H has a non-positive continuous Δ-partial derivative ![]() with respect to the second variable. Furthermore, let
with respect to the second variable. Furthermore, let ![]() be a rd-continuous function, and satisfies
be a rd-continuous function, and satisfies
![]()
Assume that there exists a positive nondecreasing Δ-differentiable function ![]() such that for every positive constant M,
such that for every positive constant M,
![]() (14)
(14)
for![]() ,
,![]() . Then (1) is oscillatory on
. Then (1) is oscillatory on![]() .
.
Proof. Suppose that ![]() is a nonoscillatory solution of (1) on
is a nonoscillatory solution of (1) on![]() . Without loss of generality, we assume that
. Without loss of generality, we assume that ![]() and
and ![]() for all
for all![]() ,
, ![]() , and we shall only consider this case. When
, and we shall only consider this case. When ![]() is eventually negative, the proof is similar. By Lemma 3, we have (23). Define the function
is eventually negative, the proof is similar. By Lemma 3, we have (23). Define the function ![]() by
by
![]() (15)
(15)
Then on![]() , we have
, we have![]() , and by (8)-(9), we obtain
, and by (8)-(9), we obtain
![]()
![]() . Based on (1) and (15), we can obtain
. Based on (1) and (15), we can obtain
![]()
by using (11), we have ![]() thus
thus
![]() (16)
(16)
By ![]() and
and![]() , we have
, we have
![]() (17)
(17)
Substituting (17) in (16), we obtain
![]() (18)
(18)
![]() . Now, due to the fact that
. Now, due to the fact that ![]() is positive and nonincreasing, there exists an
is positive and nonincreasing, there exists an ![]() sufficiently large such that
sufficiently large such that ![]() for some positive constant M and
for some positive constant M and![]() , and we have
, and we have![]() , so that
, so that
![]() (19)
(19)
Substituting (19) into (18), we obtain
![]() (20)
(20)
where![]() . Thus, for every
. Thus, for every ![]() with
with![]() , by (10), we obtain
, by (10), we obtain
![]() (21)
(21)
By (21), we obtain
![]()
From the above inequality, denoting![]() , we obtain
, we obtain
![]()
The above inequality implies that
![]()
So we have a contradiction to the condition (14). This completes the proof.
Remark 1 From Theorem 1, we can obtain different conditions for oscillation of all solutions of (1) with different choices of ![]() and
and![]() . For example,
. For example, ![]() or
or![]() .
.
Now, let us consider the function ![]() defined by
defined by
![]()
Then ![]() for
for![]() , and
, and![]() ,
, ![]() for
for![]() ,
,![]() . Furthermore,
. Furthermore,
the function h with ![]() for
for![]() ,
,![]() . Hence we have the following results.
. Hence we have the following results.
Corollary 1 Assume that the conditions (H1) - (H5), (2) hold and![]() . Furthermore, assume that there exists a positive nondecreasing Δ-differentiable function
. Furthermore, assume that there exists a positive nondecreasing Δ-differentiable function ![]() such that for every positive constant M and
such that for every positive constant M and![]() ,
,
![]() (22)
(22)
for![]() ,
,![]() . Then (1) is oscillatory on
. Then (1) is oscillatory on![]() .
.
Now, when (3) holds, we give the oscillatory criteria of Philos-type for (1).
Theorem 2 Assume that the conditions (H1) - (H5), (3) hold and![]() , and let H, h and
, and let H, h and ![]() be defined as in Theorem 1 and the condition (14) holds. Furthermore, assume that for every
be defined as in Theorem 1 and the condition (14) holds. Furthermore, assume that for every![]() ,
,
![]() (23)
(23)
where
![]()
Then (1) is oscillatory on![]() .
.
Proof. Suppose that ![]() is a nonoscillatory solution of (1) on
is a nonoscillatory solution of (1) on![]() . Without loss of generality, we assume that
. Without loss of generality, we assume that ![]() and
and ![]() for all
for all![]() ,
, ![]() , and we shall only consider this case. When
, and we shall only consider this case. When ![]() is eventually negative, the proof is similar. Since
is eventually negative, the proof is similar. Since ![]() is decreasing, it is eventually of one sign and hence
is decreasing, it is eventually of one sign and hence ![]() is eventually of one sign. Thus, we shall distinguish the following two cases:
is eventually of one sign. Thus, we shall distinguish the following two cases:
(1) ![]() for
for![]() ; and
; and
(2) ![]() for
for![]() .
.
Case (1). The proof when ![]() is an eventually positive is similar to that of the proof of Theorem 1 and it hence is omitted.
is an eventually positive is similar to that of the proof of Theorem 1 and it hence is omitted.
Case (2). For![]() , we have
, we have
![]()
and hence
![]() (24)
(24)
Integrating (24) from ![]() to
to ![]() and letting
and letting ![]() yields
yields
![]()
and thus
![]() (25)
(25)
where![]() . Using (25) in Equation (1), we find
. Using (25) in Equation (1), we find
![]() (26)
(26)
Integrating (26) from t1 to t, we have
![]()
so that
![]() (27)
(27)
Integrating (27) from t1 to t, we obtain
![]()
by (23), which is a contradiction. This completes the proof. ![]()
Remark 2 In the past, the usual result is that the condition (3) was established, then every solution of the Equation (1) is either oscillatory or converges to zero. But now Theorem 2 in our paper prove that if the condition (3) is satisfied, every solution of the Equation (1) is oscillatory.
Similar to the Corollary 1, by applying Theorem 2 with
![]()
we have the following results.
Corollary 2 Assume that the conditions (H1) - (H5), (3), (22), (23) hold and![]() , then (1) is oscillatory on
, then (1) is oscillatory on![]() .
.
Next, we give a result of a succinctness and convenient to application.
Theorem 3 Assume that the conditions (H1) - (H5), (2) hold and![]() , and let
, and let ![]() be a rd-continuous function such that
be a rd-continuous function such that
![]()
and H has a non-positive continuous Δ-partial derivative ![]() with respect to the second variable. Furthermore, assume that there exists a positive Δ-differentiable function
with respect to the second variable. Furthermore, assume that there exists a positive Δ-differentiable function ![]() such that for every positive constant M,
such that for every positive constant M,
![]() (28)
(28)
for![]() ,
,![]() . Then (1) is oscillatory on
. Then (1) is oscillatory on![]() .
.
Proof. Suppose that ![]() is a nonoscillatory solution of (1) on
is a nonoscillatory solution of (1) on![]() . Without loss of generality, assume that
. Without loss of generality, assume that ![]() and
and ![]() for all
for all![]() ,
, ![]() , which we shall only consider this case. When
, which we shall only consider this case. When ![]() is eventually negative, the proof is similar. Proceeding as in the proof of Theorem 1, we obtain (20), thus
is eventually negative, the proof is similar. Proceeding as in the proof of Theorem 1, we obtain (20), thus
![]() (29)
(29)
for all![]() . Then from (29), we have
. Then from (29), we have
![]()
for all![]() , and therefore, for all
, and therefore, for all![]() ,
,
![]()
and hence, for all![]() ,
,
![]()
Thus
![]()
which is contradicted with (28). This completes the proof. ![]()
Now, applying Theorem 3 with
![]()
we have the following results.
Corollary 3 Assume that the conditions (H1) - (H5), (2) hold and![]() . If there exists a positive Δ-differentiable function
. If there exists a positive Δ-differentiable function ![]() such that for every positive constant M and
such that for every positive constant M and![]() ,
,
![]() , (30)
, (30)
for![]() ,
,![]() . Then (1) is oscillatory on
. Then (1) is oscillatory on![]() .
.
Using the same ideas as in the proof of Theorem 2, when (3) holds, we can now obtain the following result.
Theorem 4 Assume that the conditions (H1) - (H5), (3), (23) hold and![]() . Furthermore, let H and
. Furthermore, let H and ![]() define the same as Theorem 3 and the condition (28) holds. Then (1) is oscillatory on
define the same as Theorem 3 and the condition (28) holds. Then (1) is oscillatory on ![]()
Now, let
![]()
we have the following results.
Corollary 4 Assume that the conditions (H1) - (H5), (3), (23), (30) hold and![]() , then (1) is oscillatory on
, then (1) is oscillatory on![]() .
.
Remark 3 Our results in this paper unify the oscillation of the second-order nonlinear delay differential equation and the second-order nonlinear delay difference equation. As an example, when![]() , the (1) becomes
, the (1) becomes
![]()
and the condition (30) becomes
![]()
then Corollary 3 extends Theorem 2.1 in [15] and Theorem 1 generalizes Theorem 2.1 in [15] . The Theorem 2 - 4 in this paper are new even for the cases ![]() and
and![]() .
.
Example 1 Consider the second-order nonlinear delay 2-difference equations
![]() (31)
(31)
Here
![]()
The conditions (H1) - (H4) and (2) are clearly satisfied, (H5) holds with L = 1. Now let ![]() for all
for all![]() , then
, then
![]()
so that (30) is satisfied as well. Altogether, by Corollary 3, the equation (31) is oscillatory.
Acknowledgements
We thank the Editor and the referee for their comments. This research is supported by the Natural Science Foundation of Shandong Province of China under Grant No. ZR2013AM003.