Jing Gao¹, Wei Wang^2
1College of Sciences, Shanghai Institute of Technology, Shanghai, China.
²Antai College of Economics and Management, Shanghai Jiao Tong University, Shanghai, China.
DOI: 10.4236/tel.2014.48079   PDF    HTML     3,107 Downloads   3,797 Views   Citations

Abstract

We consider LM tests for spatial correlations in the spatial error model (SEM) and spatial autoregressive model (SAM) with randomly missing data in the dependent variable. We derive the formulas of the LM test statistics and provide finite sample performance of the LM tests through Monte Carlo experiments.

Keywords

LM Test, Spatial Correlations, Missing Data, Dependent Variable

Share and Cite:

1. Introduction

Spatial models have a long history in regional science and geography (see [1] , for example). Recently, many economic processes that concern spatial correlations have been drawn more and more attention. Examples include housing decision, technology adoption, tax competition, welfare participation, and price decision. Therefore, spatial correlations are of much interest in the study of urban, environmental, labor, and developmental economics among others. Various spatial econometric models are currently being applied, among which the most popular ones are the spatial error model (SEM) and spatial autoregressive model (SAM). Before setting up a spatial econometric model and doing estimation, people tend to test the existence of the spatial correlations first. The LM tests for spatial correlations have already been developed by [2] and [1] for the SEM and the SAM. However, these tests are designed for models with fully observed data.

In practice, missing data are a common problem that researchers face. When there are missing data, the spatial econometric models will be difficult to handle due to the interdependence among the components of the error term/dependent variable vector (see [3] , for example). Therefore, the LM tests proposed by [2] and [1] will be no longer valid when missing data problem occurs. In this paper, we consider a case in which observations are randomly missing only from the dependent variable and study the LM tests for spatial correlations in this situation. This situation could be very common in regional studies, where exogenous variables may be available from different sources rather than from data available on a local government web site, but the dependent variable may have missing data. LeSage and Pace [4] and [3] [5] have considered this situation and study the estimations of the spatial econometric models¹. In this study, we focus on the tests of spatial correlations in both SEM and SAM.

The rest of the paper is organized as follows. Section 2 provides the SEM model specification with missing data in the dependent variable and LM test for the spatial correlation. We derive the formula of the LM test statistic, which is asymptotically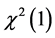. In Section 3, we study the SAM model and provide the LM test. Some Monte Carlo experiments are carried out in Section 4, and Section 5 concludes the paper.

2. LM Test for Spatial Correlation in the SEM

The Spatial Error Model is:

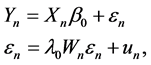(1)

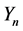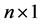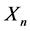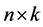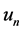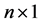where is an vector of outcomes of n cross sectional units; is an matrix of exogenous variables representing the n units’ exogenous characters; is an vector of i.i.d. disturbances with zero mean and a finite variance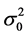; 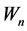is an 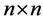spatial weights matrix of known constants with a zero diagonal; and 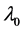is the spatial effect coefficient that measures the spatial autocorrelation on.

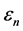If the data are fully observed, we may test

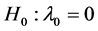
for spatial autocorrelation. Burridge [2] and [1] derived the LM test statistic as

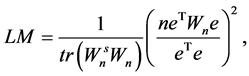
where 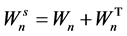and e is the OLS residual of model (1), i.e., with.

However, if there are missing observations on, the above test statistic could not be computed.

We consider the case where some of the observations in the outcome vector are unavailable. Without loss of generality, we assume that the outcomes of the last n₁ units are missing, where 0 < n₁ < n. Therefore, we can write

where is the n₂ × 1 subvector of observed outcomes, where, and is the remaining n₁ × 1

subvector of unobserved (missing) outcomes. So the (population) system under consideration is

(2)

Note that, where is a selection matrix which picks the unobserved elements

from the whole vector. Similarly, where. To simplify some of the nota-

tions, denote. Then we can write as

. (3)

The maximum likelihood (ML) approach can be based on the above equation. Let, then

, where with. Let, with being the true pa-

rameter value. Under normality, the log likelihood function is

where with. The expressions for the elements of the score

vector are:

(4)

(5)

and

(6)

where, and. The second order derivatives are, for the rele-

vant combinations of parameters, Equations (A.1)-(A.6) in the Appendix. Thus the elements of the information matrix are,

(7)

(8)

(9)

To perform the LM test, expressions (4)-(6) and (7)-(9) need to be evaluated under constrained estimation,

i.e., with the parameter values included in the null hypothesis set to zero (namely,), and with the other

parameters set to their ordinary-least-squares estimates, i.e., and

with.

Note that and

because has a zero diagonal. Thus we have the score vector as follows

where is the ordinary-least-squares residual of model (3). And the estimated information matrix is

Therefore, the LM test statistic is

with and.

Under the null, we have.

3. LM Test for Spatial Correlation in the SAM

The Spatial Autoregressive Model is:

(10)

where all the notations have same meanings as those in the previous section, except that now is an vector of i.i.d. disturbances with zero mean and a finite variance. We can see that in this model, the spatial correlations exist among the components of instead of, compared with SEM.

We consider testing the spatial lag dependence of the model, namely testing the null hypothesis

If the data are fully observed, by using the likelihood function [1] , derived the LM test statistic explicitly as

where e is the OLS residual of model (10) under the null, and

We consider the case where some of the observations in the outcome vector are unavailable. By adopting the same notations as those in the previous section, the (population) system under consideration can be written as

(11)

The reduced form equation of (11) for write is

(12)

and therefore, the ML approach based on this reduced form equation can be applied. Under normality, the log likelihood function is

The expressions for the elements of the score vector are

(13)

(14)

and

(15)

where. The second order derivatives are, for the relevant combinations of para-

meters, equations (A.7)-(A.12) in the Appendix. Thus the elements of the information matrix are,

(16)

(17)

(18)

(19)

(20)

To perform the LM test, expressions (13)-(15) and (16)-(20) need to be evaluated under constrained esti-

mation, i.e., with the parameter values included in the null hypothesis set to zero (namely,), and with

the other parameters set to their ordinary-least-squares estimates, i.e.,

and with.

Note that and

because has a zero diagonal. Thus we have the score vector as follows

where is the ordinary-least-squares residual of model (12) with. And the estimated infor-

mation matrix is

Using the formula of the inverse of a partitioned matrix, we have

Therefore, the LM test statistic is

where

with and.

Under the null, we have.

4. Monte Carlo Experiments

To investigate the finite sample performance of the LM tests, we conduct Monte Carlo experiments, designed as follows.

4.1. LM Tests in SEM

The model has two regressors and. The ()'s are independent for all i. The true slope parameters

are and. The’s are independently drawn from and are independent of and

. and are generated from.

For weights matrix, we follow the design of [6] and [3] , which is referred to as the “circular world matrix.” The weights matrix is designed as follows. For the weights matrix, the first n/3 rows (except for the first row) have zeroes everywhere, except for the elements in positions (i, i + 1) and (i, i ‒ 1). In the first row, the non-zero elements are in positions (1, 2) and (1, n) so that it relates to a circular world. The nonzero elements in the first n/3 rows are all random draws from; i.e., we allow the neighbors to asymmetrically affect one another². Then, these rows are row normalized, so that the sum of each row is equal to 1. The next n/3 rows (say,) have zeroes everywhere, except in positions (j, j ± r), where. The nonzero elements are designed in the same fashion as those in the first n/3 rows. The last n/3 rows are defined in a similar manner to the first n/3 rows. Specifically, the nonzero elements in rows are in positions (j, j+1) and (j, j‒1); in the last row, the nonzero elements are in positions (n, 1) and (n, n ‒ 1). The nonzero elements in these rows are also designed in the same fashion as those in the first 2n/3 rows. The weights matrix is a sparse weights matrix, with each individual having only several “neighbors.” The number of neighbors differs for each individual, depending on its position.

For sample sizes, we set n from “small”, n = 60 and “moderate”, n = 180, to “large”, n = 540. For missing observations, the’s of the first percent of the n individuals are unobserved for each sample size n, where is set as 10, 25, and 50.

For each n and (percentage of missing) combination, we report the percentages of rejecting the null hypothesis in all the 1000 Monte Carlo replications, for different nominal sizes 1%, 5% and 10%. The first row shows the results for the case, and the second and third row show those for and 0.5, respectively.

Tables 1-3 below show the finite performance of the LM test in the SEM. The empirical levels (first row) of the LM test are close to the theoretical ones. But for the powers (second and third row), they depend on the sample sizes and the value of. For small value of, the powers are poor, especially for small n. For larger, the powers are good, except for small n.

4.2. LM Tests in SAM

In the SAM, we generate’s independently from and independent of’s. All other designs are the same as those in the previous subsection. Tables 4-6 show the results of the LM test. The empirical levels are all close to the theoretical ones. But for the powers, they are not good for small value of when sample sizes are small. For large value of and larger sample sizes, the powers are good.

5. Conclusion

In this paper, we extend the LM tests for spatial correlations to the case where there are missing data in the dependent variable. We considered the spatial error model as well as the spatial autoregressive model and derived the formulas of the LM test statistics in both models. Monte Carlo experiments show good finite sample performance of the tests. The empirical levels of the LM tests are close to the theoretical ones and the powers are good for large sample sizes.

Appendix

The second order derivatives are, for the relevant combinations of parameters of the log likelihood function for the SEM,

(A.1)

(A.2)

(A.3)

(A.4)

(A.5)

and

(A.6)

The second order derivatives are, for the relevant combinations of parameters of the log likelihood function for the SAM,

(A.7)

(A.8)

(A.9)

(A.10)

(A.11)

and

(A.12)

NOTES

¹LeSage and Pace [4] consider an example of housing prices, where the unsold properties have known characteristics. Examples of Wang and Lee [3] [5] include censuses that provide regional demographic data, which can be aggregated to regional-level data.

²Wang and Lee [3] generate the symmetric settings in [6] to allow for asymmetry.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Anselin, L. (1988) Spatial Econometrics: Methods and Models. Kluwer, Dordrecht. http://dx.doi.org/10.1007/978-94-015-7799-1
[2]	Burridge, P. (1980) On the Cliff-Ord Test for Spatial Autocorrelation. Journal of the Royal Statistical Society, 42, 107-108.
[3]	Wang, W, and Lee, L. (2013a) Estimation of Spatial Autoregressive Models with Randomly Missing Data in the Dependent Variable. Econometrics Journal, 16, 73-102. http://dx.doi.org/10.1111/j.1368-423X.2012.00388.x
[4]	LeSage, J. and Pace, R.K. (2004) Models for Spatially Dependent Missing Data. Journal of Real Estate Finance and Economics, 29, 233-254. http://dx.doi.org/10.1023/B:REAL.0000035312.82241.e4
[5]	Wang, W, and Lee, L. (2013) Estimation of Spatial Panel Data Models with Randomly Missing Data in the Dependent Variable. Regional Science and Urban Economics, 43, 521-538. http://dx.doi.org/10.1016/j.regsciurbeco.2013.02.001
[6]	Arraiz, I., Drukker, D., Kelejian, H. and Prucha, I. (2008) A Spatial Cliff-Ord-Type Model with Heteroskedastic Innovations: Small and Large Sample Results. CESIFO Working Paper No. 2485.