Study of Stability Analysis for a Class of Fourth Order Boundary Value Problems ()
1. Introduction
The determination process for the numerical solution of initial value problems in ordinary differential equations can be classified into two categories-single step methods and multistep methods. Single step methods are those in which the approximation for the point  involves information from only one of the previous points
involves information from only one of the previous points . Methods using the approximation at more than one previous points to determine the approximation at the next point are called multistep methods. Thus a k-step method requires information about the solution at k points
. Methods using the approximation at more than one previous points to determine the approximation at the next point are called multistep methods. Thus a k-step method requires information about the solution at k points  to compute the solution at the point
to compute the solution at the point . Finite difference methods for boundary value problems are discussed in [1] . Linear multi step methods of second order differential equations are discussed in [2] . The methods based on numerical differentiation for first-order differential equations have been shown to be stiffly stable by Gear [3] . A detailed study of the single step and multistep methods has been carried out by Gear [3] , Gragg and Statter [4] and Henrici [5] . Gear [3] and Peter Henrici [5] have derived special multistep methods based on numerical integration and numerical differentiation for solving first-order differential equations. Jain [6] has considered high order stiffly stable methods. Further information can be had from [7] and [8] . Special multistep methods based on numerical differentiation for solving the initial value problem have been derived in Rama Chandra Rao [9] . The methods now to be discussed are based on replacing the function
. Finite difference methods for boundary value problems are discussed in [1] . Linear multi step methods of second order differential equations are discussed in [2] . The methods based on numerical differentiation for first-order differential equations have been shown to be stiffly stable by Gear [3] . A detailed study of the single step and multistep methods has been carried out by Gear [3] , Gragg and Statter [4] and Henrici [5] . Gear [3] and Peter Henrici [5] have derived special multistep methods based on numerical integration and numerical differentiation for solving first-order differential equations. Jain [6] has considered high order stiffly stable methods. Further information can be had from [7] and [8] . Special multistep methods based on numerical differentiation for solving the initial value problem have been derived in Rama Chandra Rao [9] . The methods now to be discussed are based on replacing the function  which is unknown, by an interpolating polynomial having the values
which is unknown, by an interpolating polynomial having the values  on a set of points xn where yn has already been computed. The methods discussed in this paper are essentially based on the idea that the solution is best approximated by polynomials. The motivation for the work carried out in this paper arises from the methods based on numerical differentiation for the first-order differential equations, special multistep methods based on numerical integration for the solution of the special second-order differential equations by Henrici [5] and Special multistep methods based on numerical differentiation for solving the initial value problem by Rama Chandra Rao [9] . In Henrici [5] methods based on Numerical Integration have been derived by integrating
on a set of points xn where yn has already been computed. The methods discussed in this paper are essentially based on the idea that the solution is best approximated by polynomials. The motivation for the work carried out in this paper arises from the methods based on numerical differentiation for the first-order differential equations, special multistep methods based on numerical integration for the solution of the special second-order differential equations by Henrici [5] and Special multistep methods based on numerical differentiation for solving the initial value problem by Rama Chandra Rao [9] . In Henrici [5] methods based on Numerical Integration have been derived by integrating  twice and replacing the function
twice and replacing the function  by an interpolating polynomial. Special multistep methods have been derived by replacing
by an interpolating polynomial. Special multistep methods have been derived by replacing  on the left hand side of
on the left hand side of by an interpolating polynomial and differentiating it four times. We have investigated a class of implicit methods. It is found that the implicit methods have order
by an interpolating polynomial and differentiating it four times. We have investigated a class of implicit methods. It is found that the implicit methods have order . Some local truncation errors are provided. The regions of absolute stability of the methods are derived. Numerical tests of the performance of the methods are established by solving differential equation and compared with the exact solution. The numerical results reported show the validity of our methods.
. Some local truncation errors are provided. The regions of absolute stability of the methods are derived. Numerical tests of the performance of the methods are established by solving differential equation and compared with the exact solution. The numerical results reported show the validity of our methods.
2. General Linear Multistep Methods for Special Fourth-Order Differential Equations
The special fourth order differential equation
 (1)
(1)
occurs frequently in many number of problems of science and engineering.
A general linear multistep method of step number k for the numerical solution of equation (1) is given by
 (2)
(2)
where aj, bj are constants and “h” is the step length.
Introducing the polynomials
 (3)
(3)
Equation (2) can be written as
 (4)
(4)
In Equation (4), “E” is the shift operator defined by 
Applying (4) to , we get the characteristic equation
, we get the characteristic equation
 (5)
(5)
The roots  of the characteristic Equation (5) and
of the characteristic Equation (5) and  are in general, complex and the region of absolute stability is defined to be the region of the complex
are in general, complex and the region of absolute stability is defined to be the region of the complex  -plane such that the roots of the characteristic Equation (5) lie within the unit circle whenever
-plane such that the roots of the characteristic Equation (5) lie within the unit circle whenever  lies in the interior of the region. Denoting the region of absolute stability of R and its boundary by
lies in the interior of the region. Denoting the region of absolute stability of R and its boundary by , the locus of
, the locus of  is given by
is given by
 (6)
(6)
3. Derivation of the Methods
Let  be the backward difference interpolating polynomial of
be the backward difference interpolating polynomial of  at
at  abscissas
abscissas . Then
. Then  is given by
is given by
 (7)
(7)
Differentiating (7) four times with respect to x, we get

Replacing  by
by  in Equation (1) and putting
in Equation (1) and putting  i.e.
i.e. , we get,
, we get,
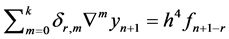 (8)
(8)
where
 (9)
(9)
Taking r = 0 in (8), a class of methods can be attained which are given by
 (10)
(10)
The coefficients  are shown in Table1
are shown in Table1
Differences in (10) are expressed in terms of function values.
After simplification, the Equation (10) will turn out into the form
 (11)
(11)
The coefficients  are shown in Table2
are shown in Table2
The local truncation error of the formula (11) is given by
 (12)
(12)

Table 1. Coefficients of ;
; .
.
It follows that the k-step method (14) has the order , which is absolutely stable for
, which is absolutely stable for 
For the method (13), we have
 . (13)
. (13)
The regions of absolute stability of the method for k = 4, 5, 6, 7, 8 and 9 are shown in Figure 1 and Figure 2 (Taking real part on x-axis and imaginary part on y-axis). The region of absolute stability is the region lying outside the boundary.

Figure 1. The region of absolute stability of the method (13) for k = 4, 5 and 6.

Figure 2. The region of absolute stability of the method (13) for k = 7, 8 and 9.
4. Numerical Example
In this section, we have applied ND methods to solve the differential equation
 (14)
(14)
in the interval  with h = 0.01 and h = 0.02 and the results are shown in Table 3 and Table4
with h = 0.01 and h = 0.02 and the results are shown in Table 3 and Table4
The fourth order numerical differentiation method derived in this paper for k = 6 is
 (15)
(15)
5. Discussion and Conclusion
The methods based on numerical integration are found to be closed regions of absolute stability; the methods

Table 3 . Solution by fifth order ND with h = 0.01.

Table 4. Solution by fifth order ND with h = 0.02.
based on numerical differentiation are found to be absolutely stable outside some closed boundaries. We have obtained the solution by numerical differentiation methods which are derived in this paper and are more accurate. The absolute errors are very small.