
1. Introduction
In 1936, Erich Hecke (see [1] ) introduced the groups  generated by two linear-fractional transformations
generated by two linear-fractional transformations
 and
and . Hecke showed that
. Hecke showed that 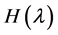 is discrete if and only if
is discrete if and only if ,
,
 ,
,  or
or . Hecke group
. Hecke group  is isomorphic to the free product of two finite cyclic group of order 2 and q, and it has a presentation
is isomorphic to the free product of two finite cyclic group of order 2 and q, and it has a presentation

The first few of these groups are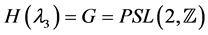 , the full modular group having special interest for mathematicians in many fields of Mathematics,
, the full modular group having special interest for mathematicians in many fields of Mathematics,  and
and .
.
A non-empty set 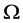 with an action of the group G on it, is said to be a G-set. We say that
with an action of the group G on it, is said to be a G-set. We say that  is a transitive G-set if, for any
is a transitive G-set if, for any 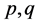 in
in  there exists a g in G such that
there exists a g in G such that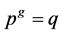 . Let
. Let , where
, where  and m is a square free positive integer. Then
and m is a square free positive integer. Then

is the set of all roots of primitive second degree equations , with reduced discriminant
, with reduced discriminant  equal to n and
equal to n and

is the disjoint union of  for all k. If
for all k. If  and its conjugate
and its conjugate  have opposite signs then
have opposite signs then  is called an ambiguous number [2] . The actual number of ambiguous numbers in
is called an ambiguous number [2] . The actual number of ambiguous numbers in  has been discussed in [3] as a function of n. The classification of the real quadratic irrational numbers
has been discussed in [3] as a function of n. The classification of the real quadratic irrational numbers  of
of  in the forms
in the forms  modulo n has been given in [4] [5] . It has been shown in [6] that the action of the modular group
modulo n has been given in [4] [5] . It has been shown in [6] that the action of the modular group , where
, where  and
and , on the rational projective line
, on the rational projective line  is transitive. An action of
is transitive. An action of , where
, where 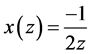 and
and  and its proper subgroups on
and its proper subgroups on  has been discussed in [7] [8] .
has been discussed in [7] [8] .
 invariant under the action of modular group G but
invariant under the action of modular group G but  is not invariant under the action of H. Thus it motivates us to establish a connection between the elements of the groups G and H and hence to deduce a common subgroup
is not invariant under the action of H. Thus it motivates us to establish a connection between the elements of the groups G and H and hence to deduce a common subgroup  of both groups such that each of
of both groups such that each of  and
and 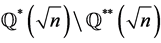 is invariant under H* and hence we find G-subsets of
is invariant under H* and hence we find G-subsets of  and H-subsets of
and H-subsets of  or
or  according as
according as  or
or  and
and 
for all non-square n. Also the partition of  has been discussed depending upon classes
has been discussed depending upon classes  modulo
modulo .
.
2. Preliminaries
We quote from [5] [6] and [8] the following results for later reference. Also we tabulate the actions on 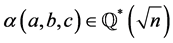 of
of  and
and , the generators of G and H respectively in Table 1.
, the generators of G and H respectively in Table 1.
Theorem 2.1 (see [5] ) Let ,
, . Then
. Then  and
and  are both G-subsets of
are both G-subsets of .
.
Theorem 2.2 (see [5] ) Let . Then
. Then  and
and  are both G-subsets of
are both G-subsets of .
.
Theorem 2.3 (see [6] ) If , then
, then  and
and  are exactly two disjoint G-subsets of
are exactly two disjoint G-subsets of  depending upon classes
depending upon classes  modulo 4.
modulo 4.
Theorem 2.4 (see [6] ) If , then
, then  and
and

Table 1. The action of elements of G and H on .
.
 are both G-subsets of
are both G-subsets of .
.
Lemma 2.5 (see [8] ) Let . Then:
. Then:
1) If  then
then  if and only if
if and only if .
.
2)  if and only if
if and only if .
.
Theorem 2.6 (see [8] ) The set , is invariant under the action of H.
, is invariant under the action of H.
Theorem 2.7 (see [8] ) For each non square positive integer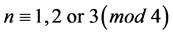 ,
,  is an H-subset of
is an H-subset of .
.
3. Action of  on
on 
We start this section by defining a common subgroup of both groups  and
and
 , where
, where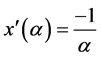 ,
,  ,
,  and
and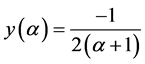 . For this, we need the following crucial results which show the relationships between the elements of G and H.
. For this, we need the following crucial results which show the relationships between the elements of G and H.
Lemma 3.1 Let 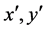 and
and  be the generators of G and H respectively defined above. Then we have:
be the generators of G and H respectively defined above. Then we have:
1)  and
and .
.
2)  and
and .
.
3)  and
and .
.
4)  and
and .
.
5)  and
and .
.
6)  and
and . In particular
. In particular  and
and .
.
Following corollary is an immediate consequence of Lemma 3.1.
Corollary 3.2 1) By Lemma 3.1, since  and
and  so
so  is a common subgroup of G and H where
is a common subgroup of G and H where  are the transformations defined by
are the transformations defined by  and
and .
.
2) As ,
,  , so
, so  is a proper subgroup of
is a proper subgroup of .
.
3)  and
and .
.
Since for each integer n, either  or
or  for each odd prime p. So in the following lemmawe classify the elements of
for each odd prime p. So in the following lemmawe classify the elements of  in terms of classes
in terms of classes  with 0 modulo p or qr, qnr nature of a, b and c modulo p.
with 0 modulo p or qr, qnr nature of a, b and c modulo p.
Lemma 3.3 Let  be prime and
be prime and . Then
. Then  consists of classes
consists of classes ,
, 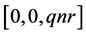 ,
,  ,
,  ,
, 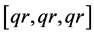 ,
,  ,
, 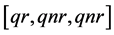 or
or .
.
Proof. Let  be any class of
be any class of . Then
. Then  leads us to exactly three cases. If
leads us to exactly three cases. If  then exactly one of
then exactly one of  is
is  and the other is qr or qnr of
and the other is qr or qnr of  as otherwise
as otherwise  and hence the class
and hence the class 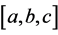 is one of the forms
is one of the forms ,
,  ,
,  ,
, . If
. If  then
then  and the class takes the form
and the class takes the form  or
or . In third case if
. In third case if  then
then  so again
so again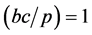 . This yields the class in the forms
. This yields the class in the forms  or
or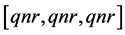 . Hence the result.
. Hence the result. 
Lemma 3.4 Let  and let
and let  be the class of
be the class of  of
of . Then:
. Then:
1) If  then
then  has the forms
has the forms ,
,  ,
,  ,
,  ,
,  ,
, 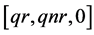 ,
,  ,
,  ,
,  ,
,  ,
,  or
or  only.
only.
2) If  then
then  has the forms
has the forms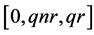 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 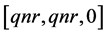 ,
,  or
or  only.
only.
Proof. Let  be the class of
be the class of  with
with . As
. As  so if
so if 
then  according as
according as  or
or . Thus we have
. Thus we have ,
, 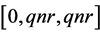 if
if  and
and ,
, 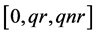 if
if . If
. If  then
then , so we get
, so we get ,
,  ,
,  ,
, 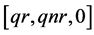 ,
, 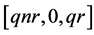 ,
,  ,
,  ,
,  ,
,  or
or  only. This proof is now complete.
only. This proof is now complete. 
Lemma 3.5 Let  and let
and let  be the class of
be the class of  of
of . Then:
. Then:
1) If then
then  has the forms
has the forms ,
,  ,
,  ,
,  ,
,  or
or  only.
only.
2) If  then
then  has the forms
has the forms ,
,  ,
,  ,
,  ,
,  or
or  only.
only.
Proof. The proof is analogous to the proof of Lemma 3.4. 
Note: If  then
then ,
,  and
and  are three classes of
are three classes of  in modulo 2. If n is an odd then three classes of
in modulo 2. If n is an odd then three classes of  are
are ,
,  and
and 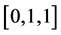 modulo 2. These are the only classes of
modulo 2. These are the only classes of 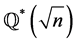 if
if . But if
. But if  then
then 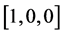 is also a class of
is also a class of  and there are no further classes. These classes in modulo 2 of
and there are no further classes. These classes in modulo 2 of 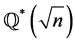 do not give any useful information during the study of action of
do not give any useful information during the study of action of  on
on  except that if
except that if  then the set consisting of all elements of
then the set consisting of all elements of 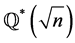 of the form
of the form  is invariant under the action of the group G. Whereas the study of action of H* on
is invariant under the action of the group G. Whereas the study of action of H* on  gives some useful information about these classes. The following crucial result determines the H*- subsets of
gives some useful information about these classes. The following crucial result determines the H*- subsets of  depending upon classes
depending upon classes  modulo 2. It is interesting to observe that
modulo 2. It is interesting to observe that 
splits into  and
and  in modulo 2. Each of these two H*-subsets further splits into proper H*-subsets in modulo 4.
in modulo 2. Each of these two H*-subsets further splits into proper H*-subsets in modulo 4.
Lemma 3.6  and
and  are two distinct H*-subsets of
are two distinct H*-subsets of  depending upon classes
depending upon classes  modulo 2.
modulo 2.
Theorem 3.7 and Remarks 3.8 are extension of Lemma 3.6 and discuss the action of H* on  depending upon classes
depending upon classes  modulo 4. Proofs of these follow directly by the equations
modulo 4. Proofs of these follow directly by the equations
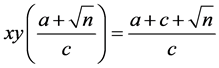 ,
,  and classes
and classes  modulo 4 given in [6] .
modulo 4 given in [6] .
Theorem 3.7 Let n be any non-square positive integer. Then 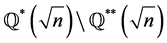 splits into two proper H*- subsets
splits into two proper H*- subsets ,
, . Similarly
. Similarly  splits into two proper H*-subsets
splits into two proper H*-subsets  and
and  .
.
Remark 3.8 1) Let . Then
. Then  and
and 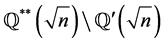 are H*-subsets of
are H*-subsets of . In particular if
. In particular if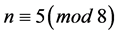 , then
, then  and
and  are H*-subsets of
are H*-subsets of . Whereas if
. Whereas if , then
, then ,
,  ,
,  and
and  are H*-subsets of
are H*-subsets of . Specifically,
. Specifically,  ,
, .
.
2) As we know that if  and
and  are even, then
are even, then  must be even as
must be even as . If
. If , then
, then  and
and .
.
3) If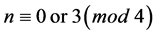 , then
, then  or
or  is empty according as
is empty according as 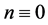 or
or . As we know that if n and c are even, then a must be even as
. As we know that if n and c are even, then a must be even as . However
. However ,
,  are proper H*-subsets of
are proper H*-subsets of  depending upon classes
depending upon classes  modulo 4.
modulo 4.
Lemma 3.9 Let n be any non-square positive integer. Then  and
and  are distinct H*-subsets of an H-set
are distinct H*-subsets of an H-set .
.
Proof. Follows by the equations  and vice versa. Hence
and vice versa. Hence  is equivalent to
is equivalent to .
.
Clearly  where
where 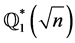 denotes the set of all ambigious numbers in
denotes the set of all ambigious numbers in
 (see [8] ).
(see [8] ).
Remark 3.10 1) Each G-subset X of  splits into two H*-subsets
splits into two H*-subsets  and
and  and
and .
.
2) Each H-subset Y of  splits into two H*-subsets
splits into two H*-subsets  and
and .
.
3) Each H-subset Y of ,
,  splits into two H*-subsets
splits into two H*-subsets  and
and .
.
4) Each H-subset Y of ,
,  splits into two H*-subsets
splits into two H*-subsets  and
and .
.
Theorem 3.11 a) If A is an H*-subset of  or
or , then
, then  is a G-subset of
is a G-subset of .
.
b) If A is an H*-subset of , then
, then  is an H-subset of
is an H-subset of  or
or  according as
according as  or
or .
.
c) If A is an H*-subset of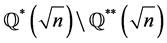 , then
, then  is an H-subset of
is an H-subset of 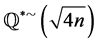 for all nonsquare n.
for all nonsquare n.
Proof. Proof of a) follows by the equation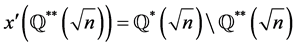 .
.
Proof of b) follows by the equations  or
or  according as
according as  or
or .
.
Proof of c) follows by the equation .
. 
Following examples illustrate the above results.
Example 3.12 1) Let . Then
. Then 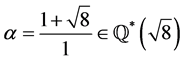 but
but . Also
. Also 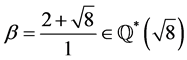 but
but . Similarly
. Similarly  whereas
whereas . Also
. Also ,
, . So
. So 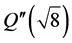 has exactly 4 orbits under the action of H whereas
has exactly 4 orbits under the action of H whereas  splits into two G-orbits namely
splits into two G-orbits namely ,
, .
.
2) 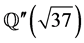 splits into nine H-orbits. Also
splits into nine H-orbits. Also  and
and  . Whereas
. Whereas  splits into four
splits into four  -orbits namely
-orbits namely ,
, 
 and
and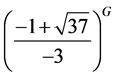 . (see Figure 1)
. (see Figure 1) 
Theorem 3.13 Let p be an odd prime factor of n. Then  and
and  are two H*-subsets of
are two H*-subsets of . In particular, these are the only H*- subsets of
. In particular, these are the only H*- subsets of  depending upon classes
depending upon classes  modulo p.
modulo p.
Proof. Let  be the class of
be the class of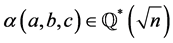 . In view of Lemma 3.3, either both of
. In view of Lemma 3.3, either both of 
are qrs or qnrs and the two equations ,
,
 fix b, c modulo p. If
fix b, c modulo p. If  then
then 
or  according as
according as  or
or . similarly for
. similarly for . This shows that the sets
. This shows that the sets  and
and  are H*-subsets of
are H*-subsets of  depending upon classes modulo p.
depending upon classes modulo p. 
The following corollary is an immediate consequence of Lemma 3.6 and Theorem 3.13.
Corollary 3.14 Let p be an odd prime and . Then
. Then  splits into four proper H*- subsets depending upon classes modulo 2p.
splits into four proper H*- subsets depending upon classes modulo 2p.
Proof. Since  implies that
implies that . This is equivalent to congruences
. This is equivalent to congruences  and
and . By Theorem 3.13
. By Theorem 3.13 ,
,  are H*-subsets and then, by Lemma 3.6, each of
are H*-subsets and then, by Lemma 3.6, each of  and
and
 further splits into two H*-subsets
further splits into two H*-subsets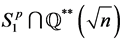 ,
,  ,
,  and
and .
. 
The next theorem is more interesting in a sense that whenever ,
,  is itself an H*-set depending upon classes
is itself an H*-set depending upon classes  modulo p.
modulo p.
Theorem 3.15 Let p be an odd prime and . Then
. Then 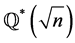 is itself an H*-set depending upon classes
is itself an H*-set depending upon classes  modulo p.
modulo p.
Proof. follows from Lemmas 3.4, 3.5 and the equations  and
and  given in Table 1.
given in Table 1.
Let us illustrate the above theorem in view of Theorem 3.4. If , then the set
, then the set
 is an H*-set.
is an H*-set.
That is,  is itself an H*-set depending upon classes
is itself an H*-set depending upon classes  modulo 3. Similarly for
modulo 3. Similarly for .
.
Theorem 3.16 Let p be an odd prime and n is a quadratic residue (quadratic non-residue) of 2p. Then  is the disjoint union of three H*-subsets
is the disjoint union of three H*-subsets ,
,  and
and  depending upon classes
depending upon classes  modulo 2p.
modulo 2p.
Proof. Follows by Theorems 2.6, 2.7 and 3.15. 
The following example justifies the above result.
Example 3.17 Since , then
, then  splits into these three H*-subsets
splits into these three H*-subsets ,
,  ,
, .
. 
The next theorem is a generalization of Theorem 3.13 to the case when n involves two distinct prime factors.
Theorem 3.20 Let  and
and  be distinct odd primes factors of n. Then
be distinct odd primes factors of n. Then ,
,  ,
,  and
and  are four H*-subsets of
are four H*-subsets of . More precisely these are the only H*subsets of
. More precisely these are the only H*subsets of  depending upon classes
depending upon classes 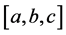 modulo
modulo .
.
Proof. Let  be any class of
be any class of  with
with . Then
. Then  implies that
implies that
 (1)
(1)
This is equivalent to congruences  and
and . By Theorem 3.14, the congruence
. By Theorem 3.14, the congruence  gives two H*-subsets
gives two H*-subsets  and
and
 of
of . As
. As , again applying Theorem 3.13 on each of
, again applying Theorem 3.13 on each of  and
and  we have four H*-subsets
we have four H*-subsets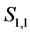 ,
,  ,
,  and
and  of
of .
.