On Bifurcation from Infinity and Multipoint Boundary Value Problems ()
1. Introduction
In this paper, we generalize and improve a result of Coyle et al. [1] about the bifurcation from infinity after stating in the line of Nussbaum [2] , Schmitt [3] , etc., a type of nonlinear Krein-Rutman theorem for a class of positively 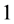 -homogeneous, compact and continuous operators in Banach spaces leaving invariant cones.
-homogeneous, compact and continuous operators in Banach spaces leaving invariant cones.
Our method is motivated by the maximum principle of Degla [4] and a result on the principal eigenvalue of multi-point Boundary Value Problems (BVP’s) of Degla [5] which allow the use of cone theoretic arguments and of the well-known general result on bifurcation from infinity; see Coyle [1] , Mawhin [6] and Rabinowitz [7] .
Furthermore, in our abstract setting, the nonlinear Krein-Rutman Theorem resets an important result on the simplicity of positive eigenvalues [8] by avoiding some inconclusive argument [8] (page 3086, lines 29-37) also misused in [9] (page 550, lines 15-27). However the gap in their arguments under their assumptions, remains an open question.
2. Preliminary Definitions and Notations
We say that a nonempty subset  of a Banach space
of a Banach space  is a cone if it is closed and 1)
is a cone if it is closed and 1) 2)
2)  and 3)
and 3) 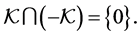
In other words, the cones considered here are closed convex cones with vertex at 0.
A cone  of a Banach space
of a Banach space  induces a partial ordering on
induces a partial ordering on  by the relation
by the relation

and it follows that

Therefore  is called an ordered Banach space with
is called an ordered Banach space with  as the positive cone of
as the positive cone of . Note that we write
. Note that we write  when
when 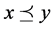 and
and ; i.e.,
; i.e.,
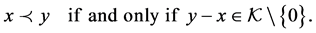
A cone 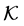 of a Banach space
of a Banach space  is said to be generating if
is said to be generating if , and total if
, and total if .
.
Given a Banach space  with dual
with dual , if a cone
, if a cone  of
of  is generating, then the set defined by
is generating, then the set defined by

is a cone of  called the dual cone of
called the dual cone of .
.
The positive cone  of an ordered Banach space
of an ordered Banach space  is said to be normal if there exists a positive constant
is said to be normal if there exists a positive constant  such that
such that

When , such an ordered Banach space is said to be monotone.
, such an ordered Banach space is said to be monotone.
Let  be an ordered Banach space. Then
be an ordered Banach space. Then
● A linear operator  is said to be positive if
is said to be positive if
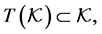
and strongly positive if
● 
● An arbitrary operator  is said to be increasing if
is said to be increasing if
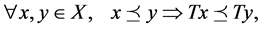
strictly increasing if
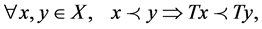
and strongly increasing if
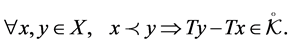
We shall say that  is increasing on
is increasing on 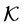 if
if
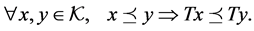
Observe that if an operator  is increasing on
is increasing on  and satisfies
and satisfies , then it leaves invariant
, then it leaves invariant .
.
Besides in our applications, we shall use the following terminology based on Degla [4] [5] , Elias [10] and Coppel [11] . Given fixed positive integers  and
and  such that
such that , and real numbers
, and real numbers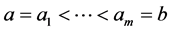 , we shall denote by
, we shall denote by  the Levin’s polynomial defined by
the Levin’s polynomial defined by  and we shall deal with disconjugate
and we shall deal with disconjugate  order differential operators on
order differential operators on  of the form
of the form

where the coefficients  are given continuous functions on
are given continuous functions on , that is, an
, that is, an 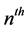 -order differential linear operator
-order differential linear operator  such that every nontrivial solution of the differential equation
such that every nontrivial solution of the differential equation  has less than
has less than  zeros counting their multiplicities.
zeros counting their multiplicities.
Recall that an  -order differential linear operator
-order differential linear operator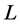 ;
;
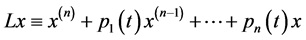
with , is disconjugate on
, is disconjugate on  if and only if
if and only if  has a Polya factorization; that is, there exist
has a Polya factorization; that is, there exist  smooth positive functions
smooth positive functions ,
,  , such that
, such that
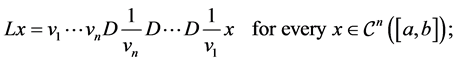
where 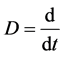
cf. [11] .
Furthermore  will denote the Green function associated to the Boundary Value Problems (in short BVP’s)
will denote the Green function associated to the Boundary Value Problems (in short BVP’s)

and besides, given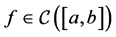 , we shall adopt the notation
, we shall adopt the notation  and
and

As in [5] , we shall also consider the Banach space
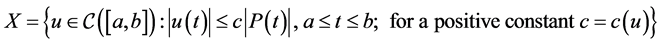
equipped with the norm
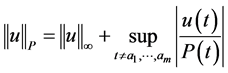
and ordered by the cone
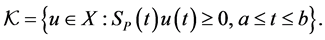
Now we are ready to state a variant of nonlinear Krein-Rutman theorems.
Proposition 1.1. Let  be a real Banach space,
be a real Banach space,  a nontrivial cone in
a nontrivial cone in  and assume that
and assume that  is a positively 1-homogeneous, compact and continuous operator.
is a positively 1-homogeneous, compact and continuous operator.
a) If  is increasing on
is increasing on  and there exist a positive vector
and there exist a positive vector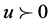 , a positive real number
, a positive real number  and a positive integer
and a positive integer , such that
, such that
 (i)
(i)
then 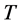 has a positive eigenvalue
has a positive eigenvalue  with a positive eigenvector.
with a positive eigenvector.
In case that  is linear, its spectral radius
is linear, its spectral radius  is such a positive eigenvalue and satisfies
is such a positive eigenvalue and satisfies
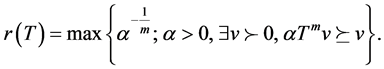
b) If  has a nonempty interior
has a nonempty interior  and
and  with the property
with the property
 (ii)
(ii)
then  has a unique positive eigenvalue and a unique positive normalized eigenvector.
has a unique positive eigenvalue and a unique positive normalized eigenvector.
In case that  is linear, this positive eigenvalue coincides with the spectral radius
is linear, this positive eigenvalue coincides with the spectral radius 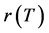 of
of , is algebraically simple and has the following variational characterization:
, is algebraically simple and has the following variational characterization:
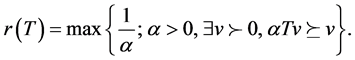
Remark 1.1. For a linear operator , the condition (ii) of b) is equivalent to
, the condition (ii) of b) is equivalent to
 (iii)
(iii)
Furthermore the conclusion of b) can be heuristically motivated by the application of the Krein-Rutman theorem to the quotient space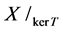 .
.
Remark 1.2. The above theorem is readily applicable to any positively  -homogeneous, compact and continuous operators that are strongly positive on the cone of an ordered Banach space.
-homogeneous, compact and continuous operators that are strongly positive on the cone of an ordered Banach space.
Remark 1.3. The proof of Theorem 2 of [8] does not fully hold but is valid for strongly increasing operators. The reason is that its conclusion (2.9) is not correct and should be read  which does not contradict the inequality (2.10) therein; that is
which does not contradict the inequality (2.10) therein; that is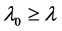 .
.
The fact is that for instance in the Banach space  ordered by the cone
ordered by the cone
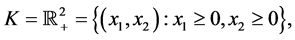
we have
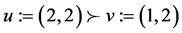
and so with 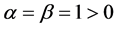 it is clear that
it is clear that
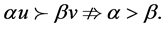
Likewise the inequality “ ” of the paragraph 4 of the proof of theorem 4.8 of [9] does not contradict the definition of “
” of the paragraph 4 of the proof of theorem 4.8 of [9] does not contradict the definition of “ ” as can be seen with
” as can be seen with 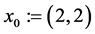 and
and  for which
for which  by simply considering again the ordered Banach space
by simply considering again the ordered Banach space .
.
Therefore we are led to raise the following Open Question: Does there exist a strictly increasing and positively 1-homogeneous compact operator of which positive eigenvalue is not simple?
Remark 1.4. For a positive compact linear operator , the condition (i) of Part a) of Proposition 1.1 is equivalent to
, the condition (i) of Part a) of Proposition 1.1 is equivalent to
 (iv)
(iv)
The following example illustrates Proposition 1.1.
Example 1.5. Consider the system of boundary value problems:
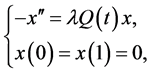
with  as a real parameter and
as a real parameter and

where the  are assumed to be nonnegative continuous functions on
are assumed to be nonnegative continuous functions on  such that on the one hand
such that on the one hand  and
and  have a common support
have a common support , and on the other hand
, and on the other hand  and
and  have a common support
have a common support  such that
such that ; i.e.
; i.e. , and where the unknown vector-valued function
, and where the unknown vector-valued function  is clearly searched in
is clearly searched in
 with zero Dirichlet boundary condition.
with zero Dirichlet boundary condition.
Then this system has a unique normalized solution with positive component functions on the interval  corresponding to a unique positive value of the parameter
corresponding to a unique positive value of the parameter .
.
Justification. We shall make use of Proposition 1.1 for the sake of illustration that may motivate other interesting works. Indeed it is immediately seen that for nontrivial solutions, we have , and the system of BVPs
, and the system of BVPs
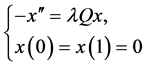
is equivalent to the integral equation

with
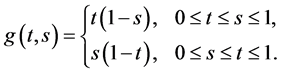
Moreover by considering the special space of continuous vector-valued functions
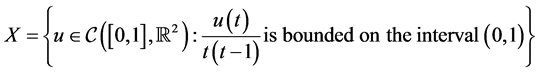
endowed with the norm 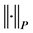 defined for any
defined for any 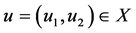 by
by
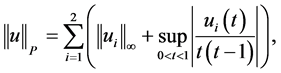
which contains all possible solutions of our eigenvalue problem, and by letting

we see that  is a normal ordered Banach space. Furthermore the non-zero linear operator
is a normal ordered Banach space. Furthermore the non-zero linear operator ;
; 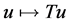 defined by
defined by
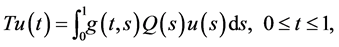
is compact and satisfies
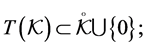
with
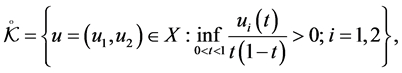
by the strong classical maximum principle.
The conclusion follows. 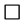
3. Bifurcation from Infinity of Conjugate Multipoint BVPs
This part can be considered as a more elaborated application of the main result of the previous section.
In the sequel we shall make use of the notations mentioned in Section 2. According to this,

equipped with the norm

and ordered by the cone
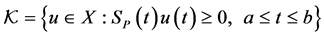
is an ordered Banach space.
Then the following theorem holds.
Theorem 2.1. Let 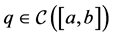 satisfy
satisfy
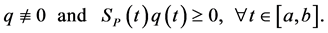
Moreover let 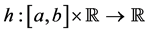 be a continuous function such that
be a continuous function such that
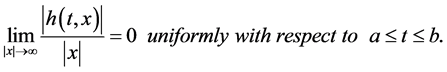
Then there exists a continuum  of positive solutions of the BVPs
of positive solutions of the BVPs
 (El)
(El)
and  such that 1) For each
such that 1) For each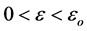 , there is a corresponding subcontinuum
, there is a corresponding subcontinuum 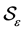 contained in
contained in
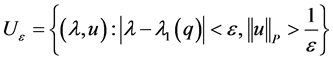
which connects  and
and .
.
2) If  with
with  as
as , then
, then

(in fact in ) to the unique normalized nontrivial solution of
) to the unique normalized nontrivial solution of
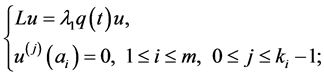
where .
.
Remark 2.2. An analogue version of Theorem 2.1 can be stated with  satisfying the following property:
satisfying the following property:

Remark 2.3. It is worth observing that Theorem 2.1 is a generalized version of a result of [1] since this Theorem 2.1 concerns multipoint conjugate boundary conditions and deals with a function  that may vanish on subintervals of
that may vanish on subintervals of 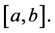
For a proof of this Theorem 2.1, we need the lemma below which can also be deduced from Proposition 1.1.
Lemma A. [5]
If  satisfies
satisfies  on a set of positive measure and
on a set of positive measure and  for a.e.
for a.e. , then the eigenvalue BVPs
, then the eigenvalue BVPs
 (Ql)
(Ql)
has a positive eigenvalue  which is simple with an eigenfunction
which is simple with an eigenfunction  such that
such that .
.
Now we recall a standard result on bifurcation theory which together with Lemma A will prove our Theorem 2.1 which is about a bifurcation from infinity for conjugate multipoint BVPs.
Lemma B. [1] [6] [7] [12]
Let  be a real Banach space with norm
be a real Banach space with norm . Assume that
. Assume that

is such that for each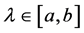 ,
,  is a compact linear operator, and for each
is a compact linear operator, and for each ,
,  is differentiable on
is differentiable on . Let
. Let 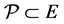 be a cone with nonempty interior,
be a cone with nonempty interior, .
.
Moreover suppose that
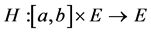
is a completely continuous map satisfying
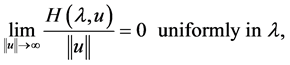
and consider the equation
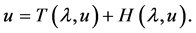
If ,
,  with
with ,
,

then there exist  and a continuum
and a continuum  such that for any
such that for any , there exists a corresponding subcontinuum
, there exists a corresponding subcontinuum  contained in
contained in
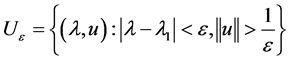
which connects  and
and . Moreover if
. Moreover if 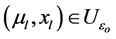 with
with  as
as ; then
; then
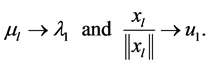
Proof of Theorem 2.1. First note that all possible solutions of the BVP’s (El) lie in  since they are of the form
since they are of the form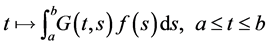 ; where
; where 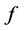 is continuous and
is continuous and 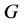 is the Green function of the BVPs
is the Green function of the BVPs
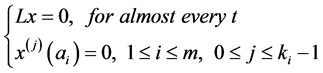
with the property that  is bounded on
is bounded on .
.
Now (El) is equivalent, by the properties of the Green function , to the following equation:
, to the following equation:

where 
and 
Moreover as seen in the proof of Lemma A [5] , the operator 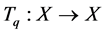 is a non-zero positive compact linear operator satisfying
is a non-zero positive compact linear operator satisfying

while 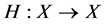 is completely continuous and satisfies
is completely continuous and satisfies

by the assumptions on . Indeed:
. Indeed:
1) We show that 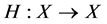 is completely continuous.
is completely continuous.
Step 1.  maps bounded subsets into compact subsets. Let
maps bounded subsets into compact subsets. Let  be a sequence of elements of
be a sequence of elements of  of which norms are bounded, say by a constant real number
of which norms are bounded, say by a constant real number . Let
. Let
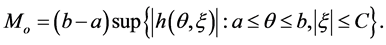
Then, on one hand,

and on the other hand, we have for all :
:
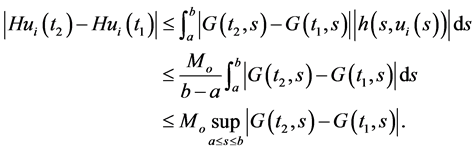
Hence for all 

where  is the modulus of continuity of
is the modulus of continuity of . Moreover as a continuous function,
. Moreover as a continuous function,  is uniformly continuous on the compact set
is uniformly continuous on the compact set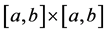 , and so
, and so . Therefore the Ascoli theorem implies the existence of a subsequence
. Therefore the Ascoli theorem implies the existence of a subsequence  of
of  such that
such that
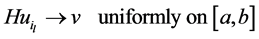
for some .
.
By applying again Ascoli theorem we see that there exists a subsequence of , still denoted by
, still denoted by , such that
, such that
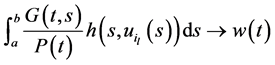
uniformly on  for a suitable
for a suitable . Indeed, to realize this claim, let
. Indeed, to realize this claim, let  and choose
and choose  satisfying
satisfying

where  is a finite upper-bound of the ratio
is a finite upper-bound of the ratio .
.
Consider now on the compact 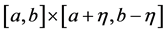 the function
the function  extending continuously the quotient function
extending continuously the quotient function . The function
. The function  is uniformly continuous on
is uniformly continuous on  and so there exists
and so there exists 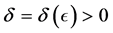 for which
for which
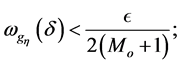
Therefore, denoting by  the continuous extension of
the continuous extension of  to
to , i.e.,
, i.e.,

we have for all  satisfying
satisfying :
:

This shows that the sequence of functions 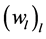 is equicontinuous on
is equicontinuous on  and proves the claim since the functions
and proves the claim since the functions  are also uniformly bounded as
are also uniformly bounded as
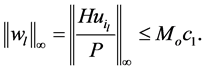
Now from the former convergence; i.e. , we deduce that for all
, we deduce that for all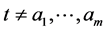 ,
,

Thus  for
for  and it follows that
and it follows that  converges to
converges to  in
in .
.
Step 2. If  converges to some
converges to some  in
in , then the Lebesgue dominated convergence theorem implies that
, then the Lebesgue dominated convergence theorem implies that  converges to
converges to  for each
for each .
.
It follows from the combination of Steps  that
that  is completely continuous; i.e.,
is completely continuous; i.e.,  maps bounded sets into compact sets and is continuous.
maps bounded sets into compact sets and is continuous.
2) We show that 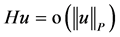 as
as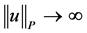 .
.
To this end, let  be arbitrary. Then by assumption there exists
be arbitrary. Then by assumption there exists  such that
such that
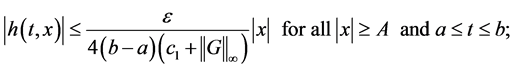
where 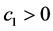 is an upper-bound of
is an upper-bound of 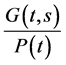 on
on . By setting
. By setting
 , we have at once
, we have at once

Therefore for every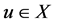 , we have on one hand
, we have on one hand
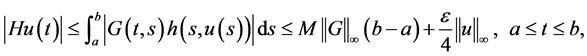
and on the other hand
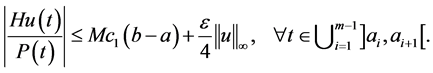
Thus

Now by putting
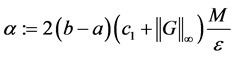
we see clearly that

That is

The result follows by applying Lemma B. 
Acknowledgements
The author is grateful to Professor R. Agarwal for having given him the opportunity to attend the International Conference on the Theory, Methods and Applications of Nonlinear Equations from the 17th to the 21st December 2012.
The author would like also to thank the Abdus-Salam International Centre for Theoretical Physics (ICTP, Trieste, Italy) for its hospitality during his first visit as a Regular Associate.