Fixed Point Theorem for Maps Satisfying a General Contractive Condition of Integral Type ()
1. Introduction
Recently, Azam et al. [1] introduced complex-valued metric space which is more general than classical metric space. Sastry et al. [2] proved that every complex-valued metric space is metrizable and hence is not real generalizations of metric spaces. But indeed it is a metric space and it is well known that complex numbers have many applications in Control theory, Fluid dynamics, Dynamic equations, Electromagnetism, Signal analysis, Quantum mechanics, Relativity, Geometry, Fractals, Analytic number theory, Algebraic number theory etc. For more detail, one can refer to [3] -[5] . The aim of this paper is to prove a common fixed point theorem for variants of weak compatible maps in a complex valued-metric space. As a consequence, we extend and generalize various known results in the literature using (CLRg) property in complex valued metric space.
2. Preliminaries
Let ℂ be the set of complex numbers and z1, z2 ∊ ℂ, recall a natural partial order relation ≾ on ℂ as follows:
 if and only if
if and only if  and
and 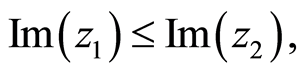
 if and only if
if and only if  and
and 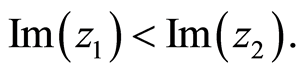
Definition 2.1. [1] . Let X be a nonempty set such that the map d: X × X → ℂ satisfies the following conditions:
(C1)  for all
for all  and
and 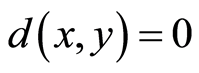 if and only if x = y;
if and only if x = y;
(C2)  for all
for all 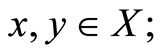
(C3)  for all
for all 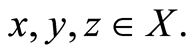
Then d is called a complex-valued metric on X, and (X, d) is called a complex-valued metric space.
Example 2.1. [1] Define complex-valued metric d: X × X → ℂ by . Then (X, d) is a complex-valued metric space.
. Then (X, d) is a complex-valued metric space.
Definition 2.2. [1] . Let (X, d) complex -valued metric space and x ∈ X. Then sequence {xn} sequence is i) convergent if for every  there is a natural number N such that
there is a natural number N such that , for all
, for all  We write it as
We write it as 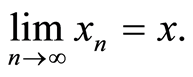
ii) a Cauchy sequence, if for every  there is a natural number N such that
there is a natural number N such that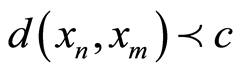 , for all
, for all 
Definition 2.3. [5] [6] . A pair of self-maps f and g of a complex-valued metric space  are weakly compatible if fgz = gfz for all z ∊ X at which fz = gz.
are weakly compatible if fgz = gfz for all z ∊ X at which fz = gz.
Example 2.2. [6] . Define complex-valued metric  defined by
defined by
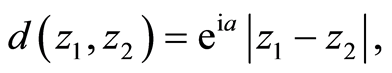
where a is any real constant. Then (X, d) is a complex-valued metric space. Suppose self maps f and g be defined as:

and

Clearly, f and g are weakly compatible self maps.
In 2011, Sintunavarat and Kumam [7] introduced a new property called as “common limit in the range of g property” i.e., (CLRg) property, defined as:
Definition 2.4. A pair (f, g) of self-mappings is said to be satisfy the common limit in the range of g property if there exists a sequence  in X such that
in X such that  for some
for some 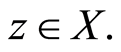
3. Main Results
Definition 3.1. Let (X, d) be a complex valued metric space and (f, g) be a pair of self mappings on X and  Let us consider the following sets:
Let us consider the following sets:

and define the following conditions:
A) For arbitrary  there exists
there exists
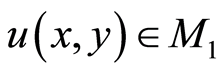
such that
 ;
;
B) For arbitrary  there exists
there exists

such that
 ;
;
C) For arbitrary  there exists
there exists
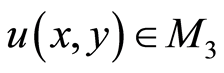
such that
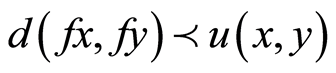 .
.
Conditions A), B) and C) are called strict contractive conditions.
Theorem 3.1. Let f and g be two weakly compatible self mappings of a complex valued metric space (X, d) such that
(3.1) f, g satisfy (CLRg) property;
(3.2) for all  there exists
there exists
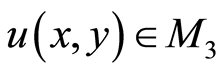
such that
 .
.
Then f and g have a unique common fixed point in X.
Proof. Since f and g satisfy the (CLRg) property, there exists a sequence {xn} in X such that  for some x
for some x  X.
X.
We first show that fx = gx. Suppose not, i.e., fx ≠ gx.
From (3.2),
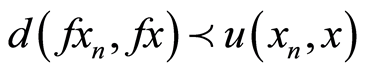 (3.3)
(3.3)
where


Three cases arises:
i) If
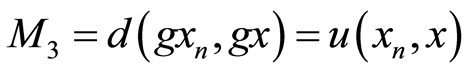
then (3.3) implies
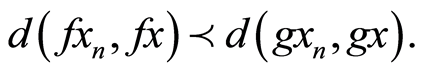
Taking limit as n→∞,

which gives,  contradiction.
contradiction.
ii) If

then (3.3) implies,
 .
.
Taking limit as n→∞,
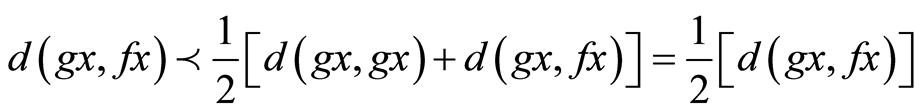
i.e.,  which gives,
which gives,  , a contradiction.
, a contradiction.
iii) If
 then (3.3) gives,
then (3.3) gives,
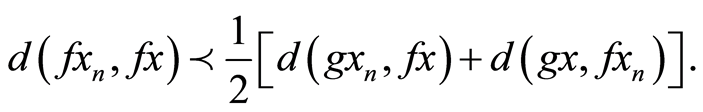
Making limit as n→∞,
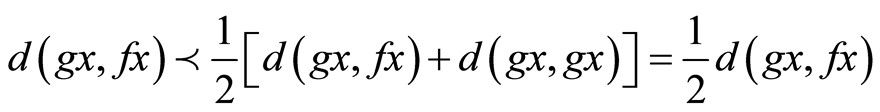
i.e.,  which gives,
which gives,  , a contradiction.
, a contradiction.
Hence, from all three cases, gx = fx.
Now let z = fx = gx. Since f and g are weakly compatible mappings fgx = gfx which implies that fz = fgx = gfx = gz.
We claim that fz = z. Let, if possible, fz ≠ z.
Now
 (3.4)
(3.4)
where
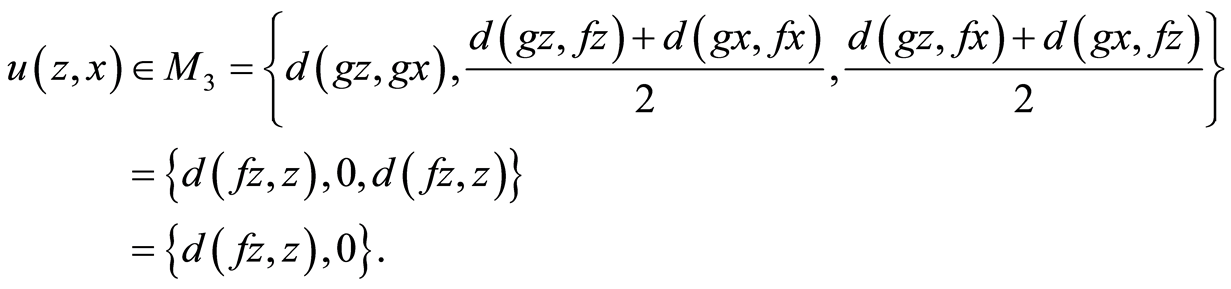
Two cases arises:
i) If , then (3.4) gives,
, then (3.4) gives,

which gives,  , a contradiction.
, a contradiction.
ii) If , then (3.4) gives,
, then (3.4) gives,
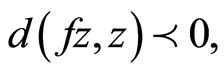
which gives,  a contradiction.
a contradiction.
Hence, from two cases, it is clear that fz = z = gz.
Hence z is a common fixed point of f and g.
For uniqueness, suppose that w is another common fixed point of f and g.
We shall prove that z = w. Let, if possible, z ≠ w.
Then
 (3.5)
(3.5)
where
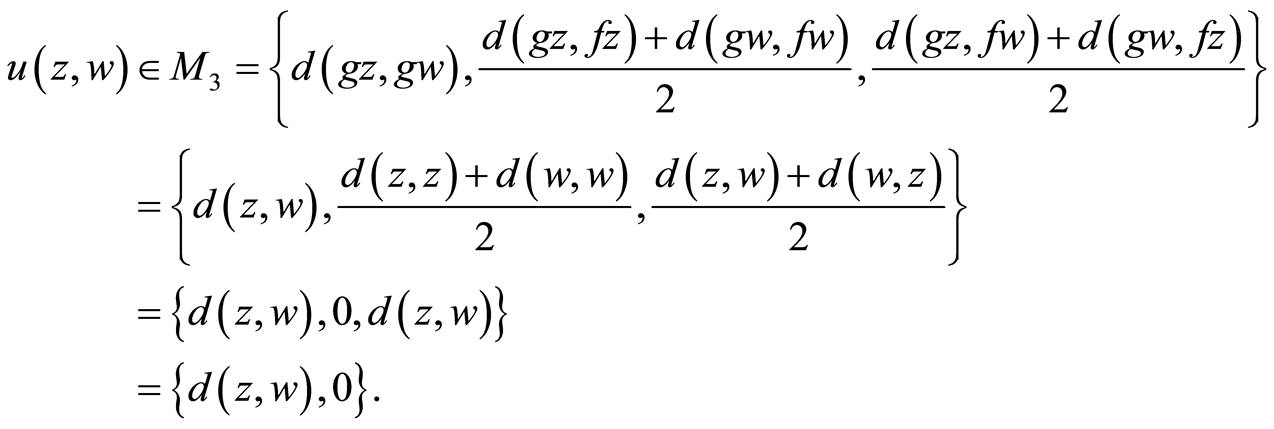
Again, two possible cases i) If , then by (3.5), we have
, then by (3.5), we have

which gives,  , a contradiction.
, a contradiction.
ii) If , then by (3.5), we have
, then by (3.5), we have

which gives,  , a contradiction.
, a contradiction.
Hence, z = w.
So, we can say that f and g have a unique common fixed point.
Remark 3.1. Theorem 3.1 also holds true if  is replaced by
is replaced by .
.
Definition 3.2. Let (X, d) be a complex valued metric space, and let f, g: X→X. Then f is called a g-quasicontraction, if for some constant  and for every x, y
and for every x, y X, there exists
X, there exists
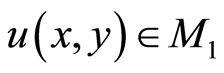
such that
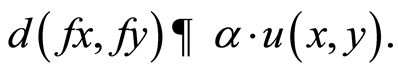
Theorem 3.2. Let f and g be two weakly compatible self mappings of a complex valued metric space (X, d) such that
(3.6) f is a g-quasi-contraction;
(3.7) f and g satisfy (CLRg) property.
Then f and g have a unique common fixed point.
Proof. Since f and g satisfy the (CLRg) property, there exists a sequence {xn} in X such that

We first claim that fx = gx. Suppose not. Since, f is a g-quasi-contraction, therefore
 (3.8)
(3.8)
for some 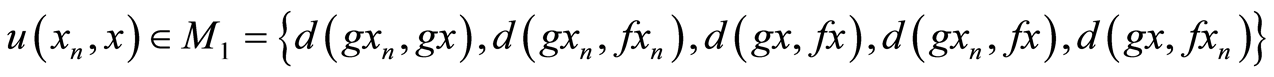
Following five cases arises:
i) If  then by (3.8), we have
then by (3.8), we have
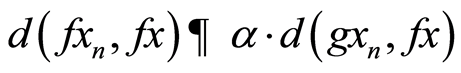
taking limit as n→∞,we have
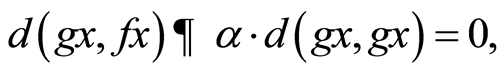
which gives, 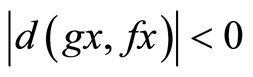 , a contradiction.
, a contradiction.
ii) If 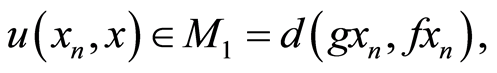 then by (3.8), we have
then by (3.8), we have
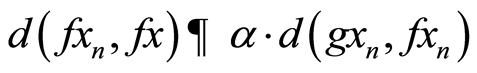
taking limit as n→∞,we have

which gives,  , a contradiction.
, a contradiction.
iii) If  then by (3.8), we have
then by (3.8), we have

taking limit as n→∞, we have
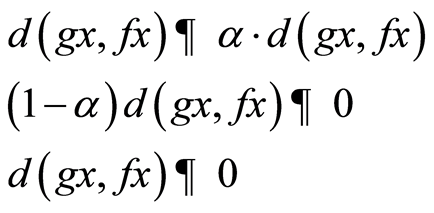
which gives,  , a contradiction.
, a contradiction.
iv) If  then by (3.8), we have
then by (3.8), we have

taking limit as n→∞,we have
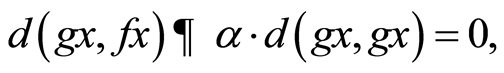
which gives,  , a contradiction.
, a contradiction.
v) If  then by (3.8), we have
then by (3.8), we have
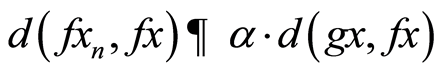
taking limit as n→∞,we have
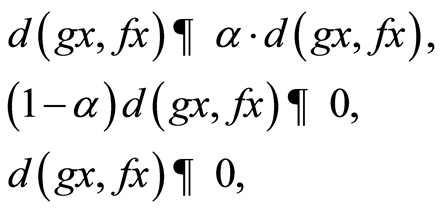
which gives,  , a contradiction.
, a contradiction.
Thus from all fives possible cases, gx = fx.
Now, let z = fx = gx. Since f and g are weakly compatible mappings fgx = gfx which implies that fz = fgx = gfx = gz.
We claim that fz = z. Suppose not, then by (3.6), we have
 (3.9)
(3.9)
where
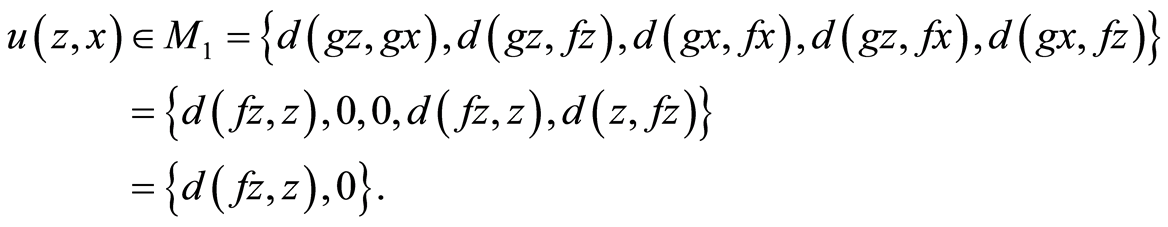
Two cases arises:
i) If  then by (3.9), we have
then by (3.9), we have

which gives,  a contradiction.
a contradiction.
ii) If , then by (3.9), we have
, then by (3.9), we have

which gives,  a contradiction.
a contradiction.
Thus, fz = z = gz.
Hence, z is a common fixed point of f and g.
For uniqueness, suppose that w is another common fixed point of f and g in X.
By (3.6), we have
 (3.10)
(3.10)
where
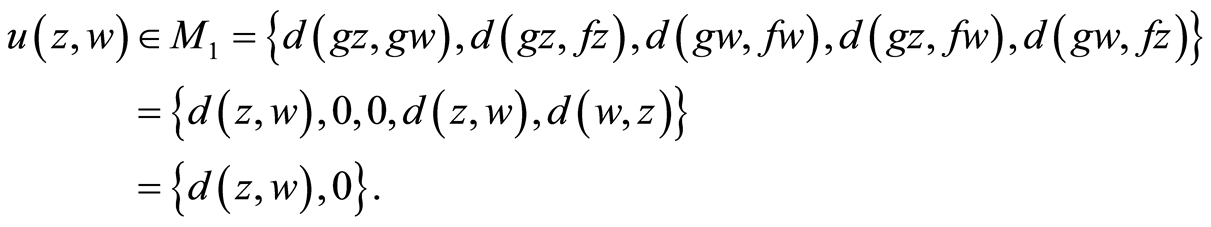
Two possible cases arises:
i) If , then by (3.9), we have
, then by (3.9), we have
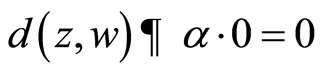
which gives , a contradiction.
, a contradiction.
ii) If 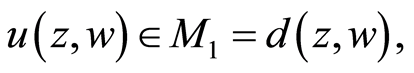 then by (3.9), we have
then by (3.9), we have

which gives , a contradiction.
, a contradiction.
Hence, z = w i.e., f and g have a unique common fixed point.
NOTES
*Corresponding author.