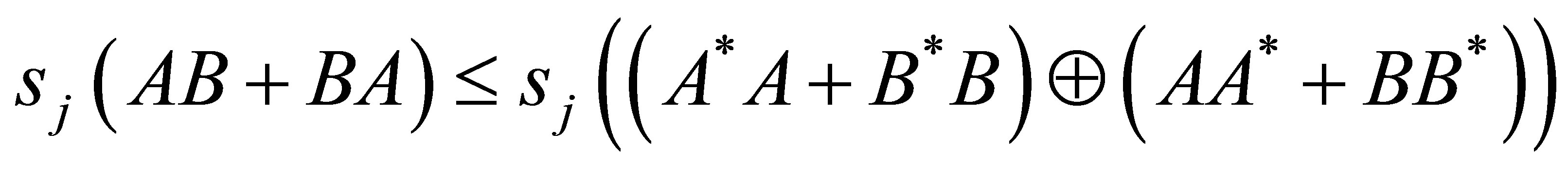1. Introduction
Let  denote the space of all bounded linear operators on a complex separable Hilbert space H, and let
denote the space of all bounded linear operators on a complex separable Hilbert space H, and let  denote the two-sided ideal of compact operators in
denote the two-sided ideal of compact operators in . For
. For , the singular values of
, the singular values of , denoted by
, denoted by  are the eigenvalues of the positive operator
are the eigenvalues of the positive operator  as
as  and repeated according to multiplicity. Note that
and repeated according to multiplicity. Note that 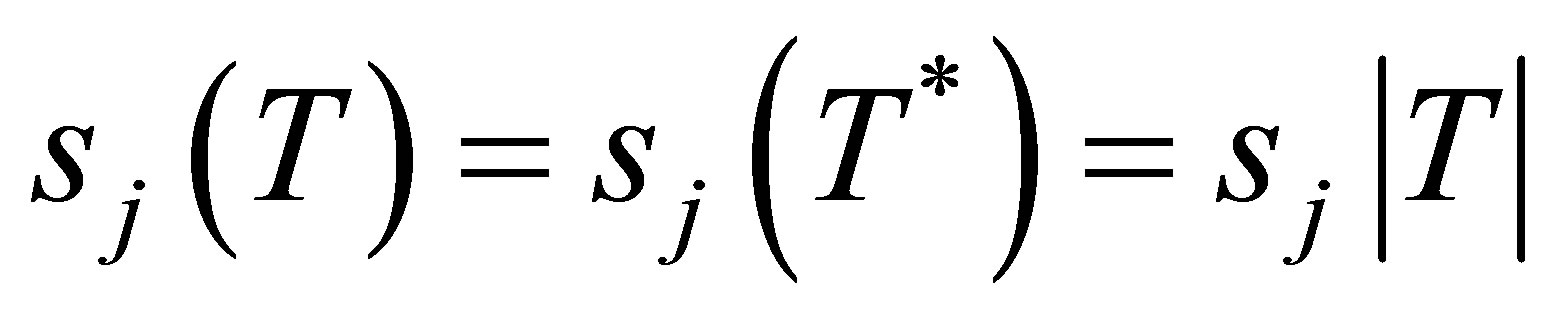
 It follows Weyl’s monotonicity principle (see, e.g., [1, p. 63] or [2, p. 26]) that if
It follows Weyl’s monotonicity principle (see, e.g., [1, p. 63] or [2, p. 26]) that if  are positive and
are positive and , then
, then 
 The singular values of
The singular values of  and
and  are the same, and they consist of those of
are the same, and they consist of those of  together with those of
together with those of  . Here, we use the direct sum notation
. Here, we use the direct sum notation  for the blockdiagonal operator
for the blockdiagonal operator 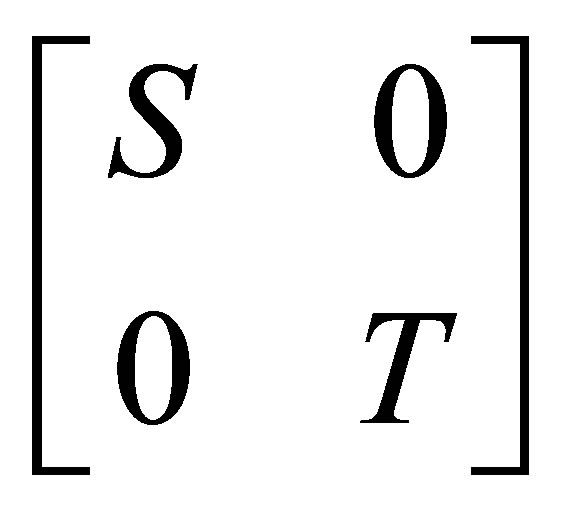 defined on
defined on .
.
The Jordan decomposition for self-adjoint operators asserts that every self-adjoint operator can be expressed as the difference of two positive operators. In fact, if 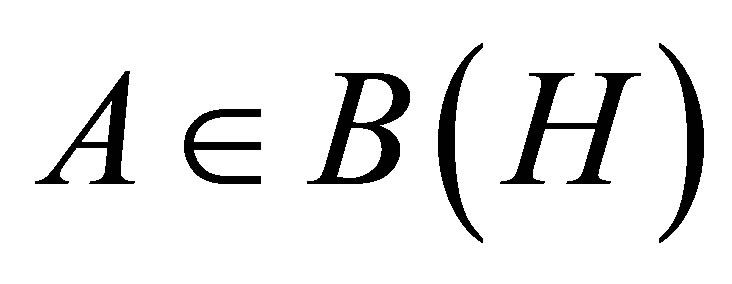 is self-adjoint, then
is self-adjoint, then  where
where
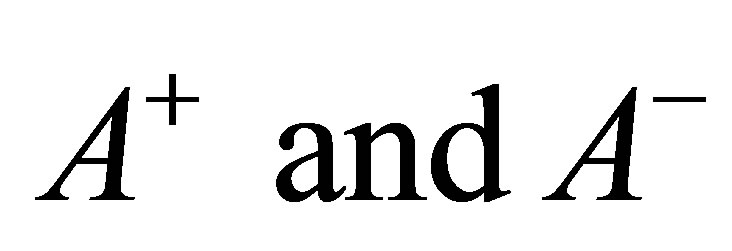 are the positive operators given by
are the positive operators given by
 and
and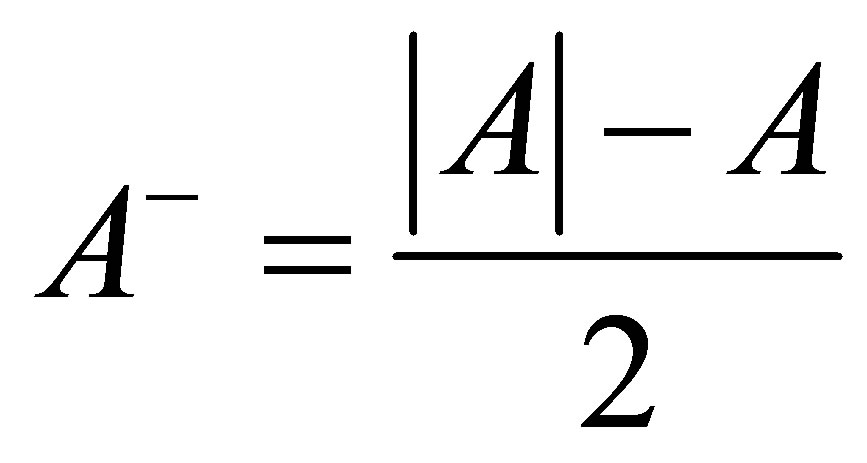 , see [1].
, see [1].
Let  be any operator, we can write
be any operator, we can write  in the form
in the form
 , where
, where 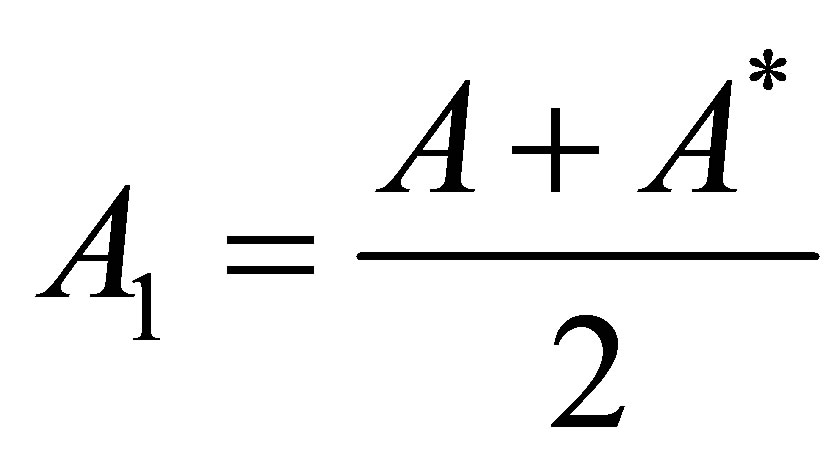 and
and  are self-adjoint operators, this is called the Cartesian decomposition of the operator
are self-adjoint operators, this is called the Cartesian decomposition of the operator . If
. If  is normal, then
is normal, then .
.
Audeh and Kittaneh have proved in [3] that if 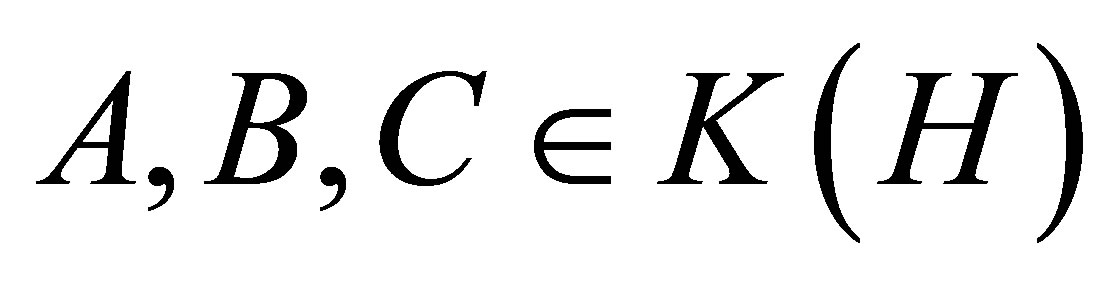 such that
such that , then
, then
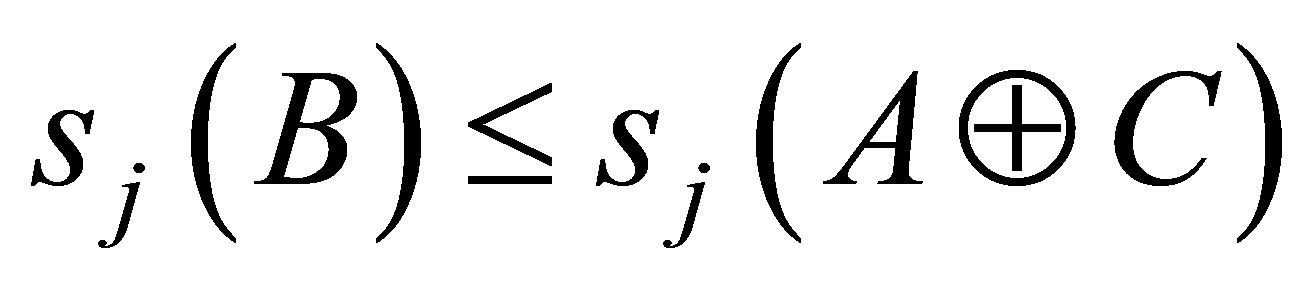 (1.1)
(1.1)
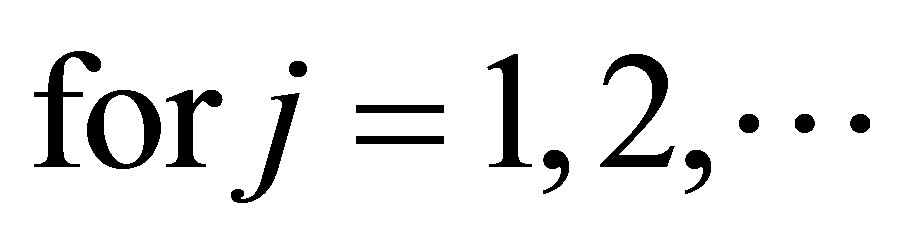
Also, Audeh and Kittaneh have proved in [3] that if 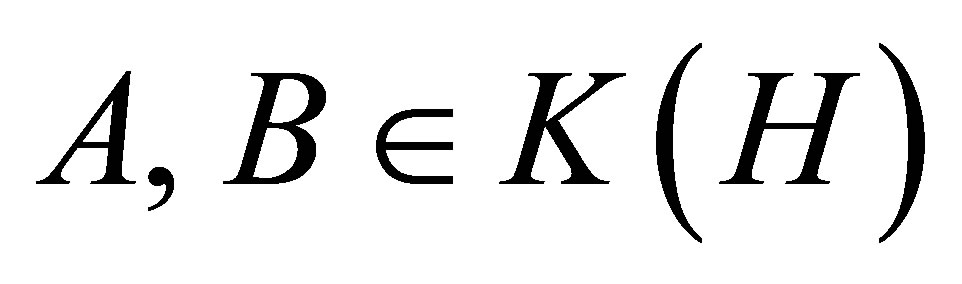 such that
such that  is self-adjoint,
is self-adjoint, 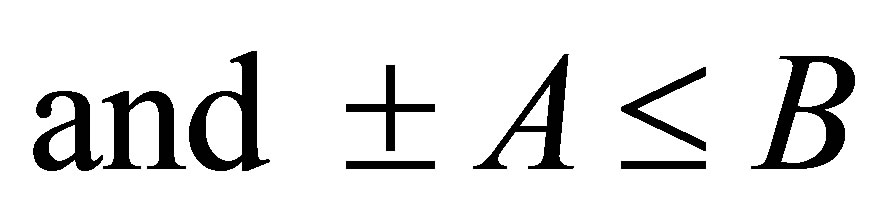
 , then
, then
 (1.2)
(1.2)
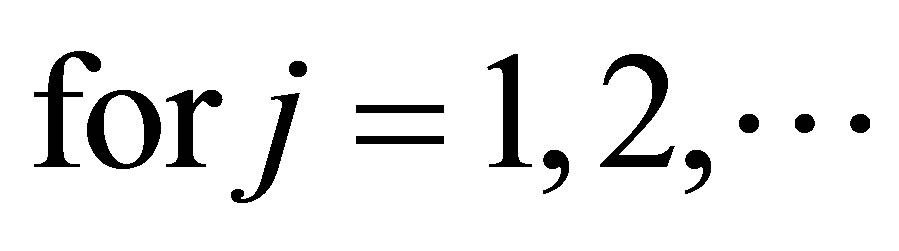
In addition to this, Audeh and Kittaneh have proved in [3] that if  be self-adjoint operators, then
be self-adjoint operators, then
 (1.3)
(1.3)

Zhan has proved in [4] that if  are positive, then
are positive, then
 (1.4)
(1.4)
 Moreover, it has proved in [3] that (1.3) is a generalization of (1.4).
Moreover, it has proved in [3] that (1.3) is a generalization of (1.4).
Hirzallah and Kittaneh have proved in [5] that if , then
, then
 (1.5)
(1.5)
In this paper, we will give singular value inequalities for normal operators:
Let  be normal operator in
be normal operator in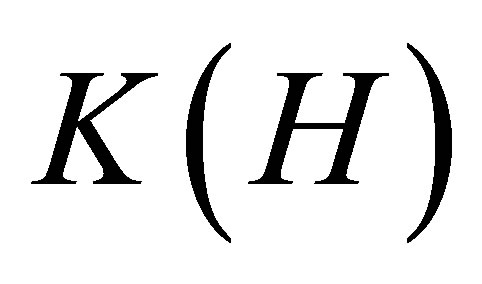 . Then
. Then
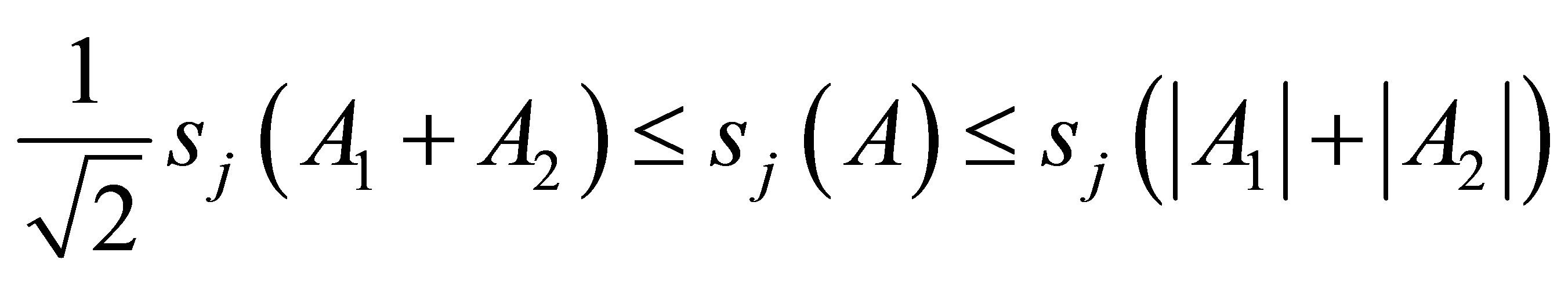 (1.6)
(1.6)

We will give singular value inequality to the normal operator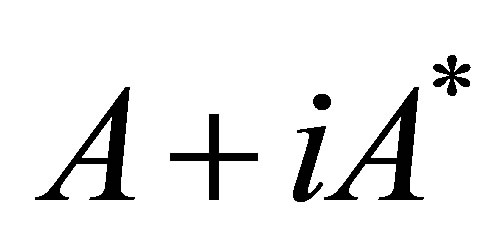 , where
, where  is normal:
is normal:
Let  be normal operator in
be normal operator in . Then
. Then
 (1.7)
(1.7)

2. Main Results
We will begin by presenting the following theorem for complex numbers Theorem 2.1. Let 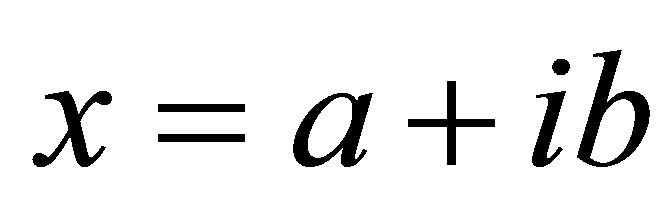 be complex number. Then
be complex number. Then
 (2.1)
(2.1)
Also,
 (2.2)
(2.2)
Proof. The right hand side of the inequalities is well known. To prove the left hand side,

Moreover, 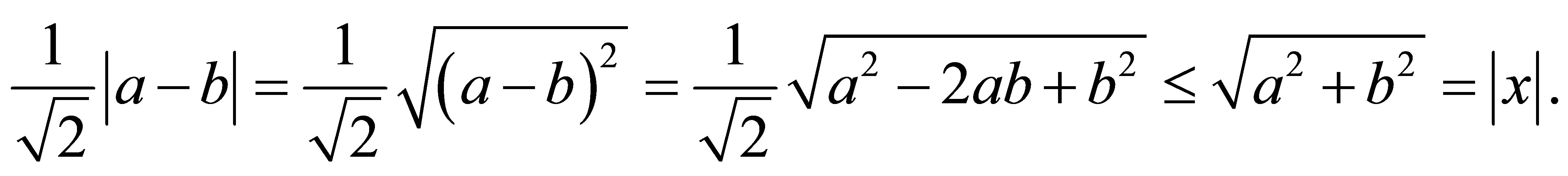
Now, we will present operator version of Theorem 2.1, inequality (2.1).
Theorem 2.2. Let  be normal operator in
be normal operator in , where
, where 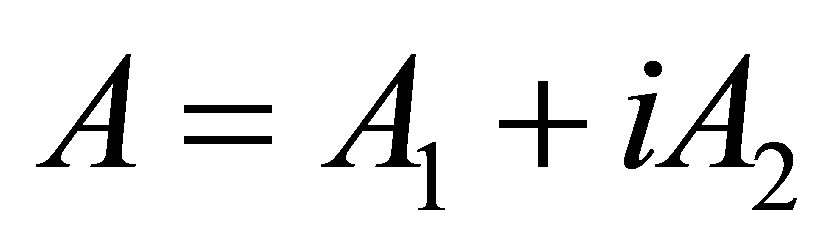 be the Cartesian decomposition of
be the Cartesian decomposition of . Then
. Then
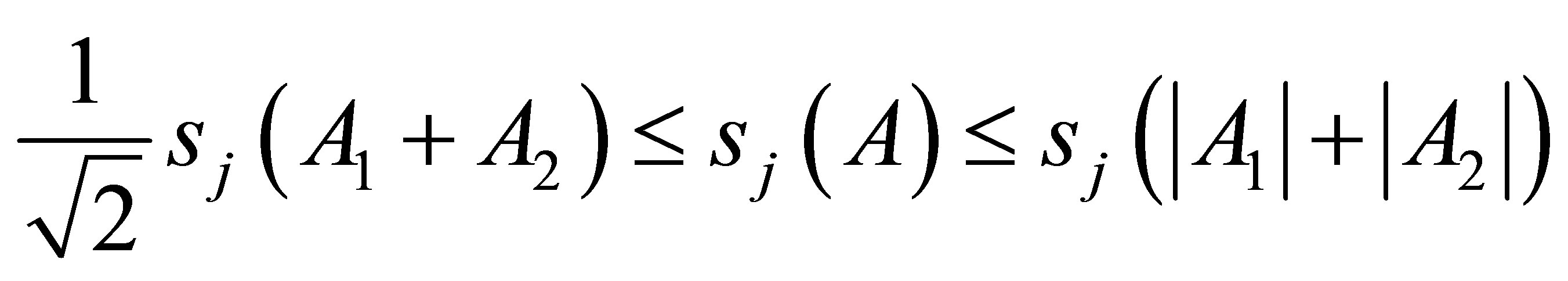
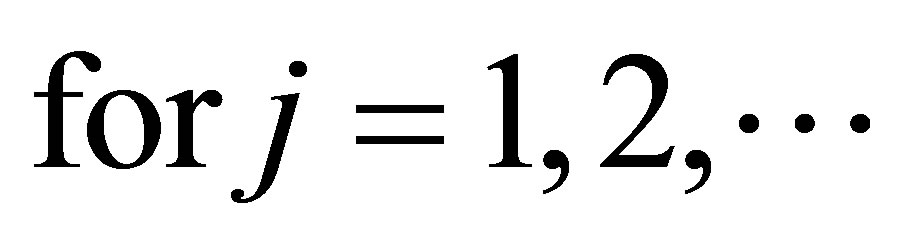
Proof. Let  be the Cartesian decomposition of the normal operator
be the Cartesian decomposition of the normal operator , which implies that
, which implies that . Now,
. Now,  , it follows that
, it follows that
 In fact
In fact  for
for
 By using Weyl’s monotonicity principle [1]
By using Weyl’s monotonicity principle [1]
and the inequality , we get the right hand side of the theorem. To prove the left hand side of the inequality, we will use the inequality which is well known for commuting self-adjoint operators and it asserts that
, we get the right hand side of the theorem. To prove the left hand side of the inequality, we will use the inequality which is well known for commuting self-adjoint operators and it asserts that
 (2.3)
(2.3)
This implies that
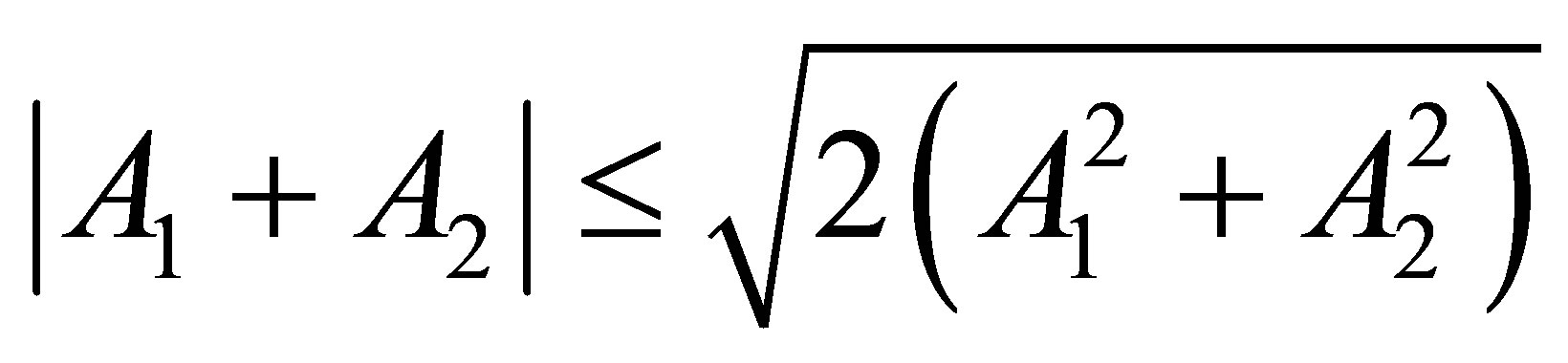 (2.4)
(2.4)
But it is known that it follows Weyl’s monotonicity principle [1] and the inequality (2.4) that
it follows Weyl’s monotonicity principle [1] and the inequality (2.4) that
 (2.5)
(2.5)
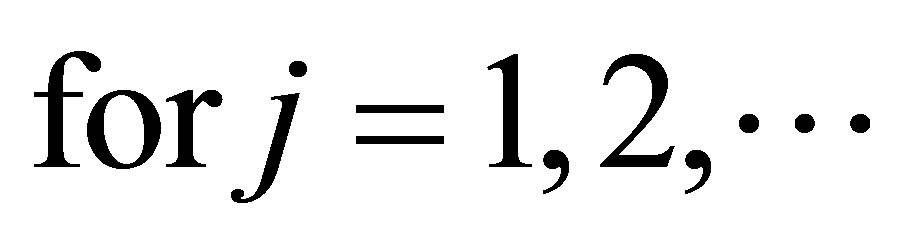
Inequality (2.5) is equivalent to saying that
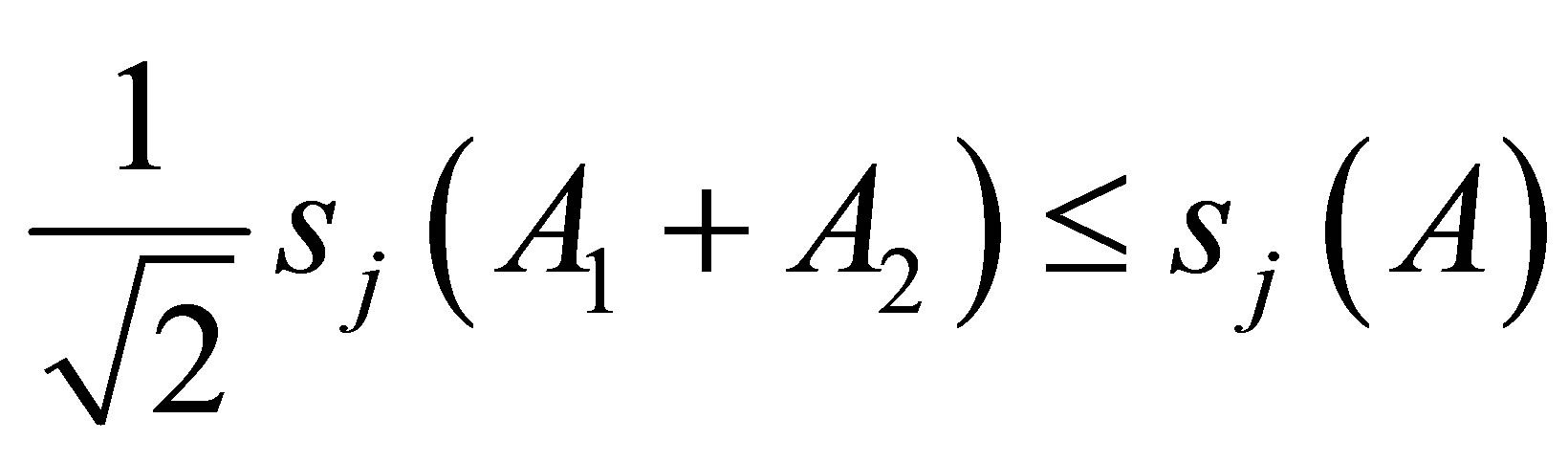

Remark 1. (i) Equality holds in the right hand side of Theorem 2.2 if either  or
or .
.
(ii) Equality holds in the left hand side of theorem 2.2 if .
.
We will present operator version of Theorem 2.1, inequality (2.2).
Remark 2. Let
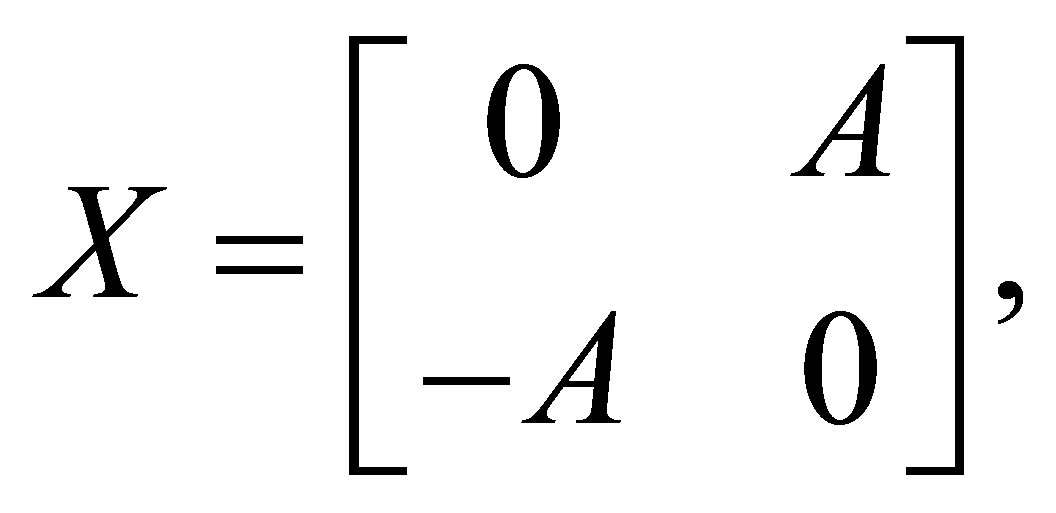
where  is normal operator. Then
is normal operator. Then  is normal operator with
is normal operator with  is the Cartesian decomposition of
is the Cartesian decomposition of .
.
 and
and .
.
It follows that , and
, and .
.
Now, by direct calculations and applying Theorem 2.2 we get
 (2.6)
(2.6)
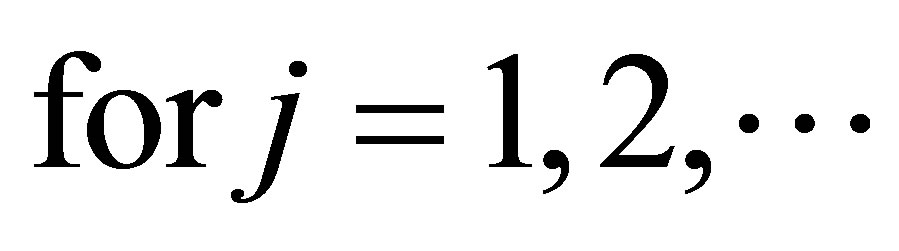
Remark 3. We note that the right hand side of the inequality (2.6) is the same as the inequality (1.6), but the left hand side of the inequalities (1.6) and (2.6) says that the singular value of the addition or subtraction of the Cartesian decomposition for the normal operator  divided by
divided by  is less than or equal to the singular value of the normal operator itself.
is less than or equal to the singular value of the normal operator itself.
As an application of the Theorem 2.2, we will determine upper and lower bounds for singular values of the normal operator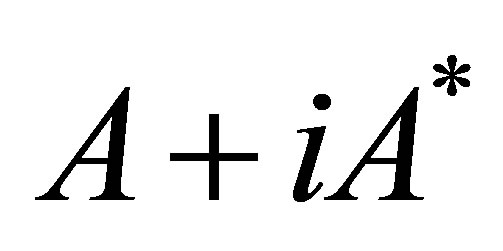 , where
, where  is normal.
is normal.
Theorem 2.3. Let 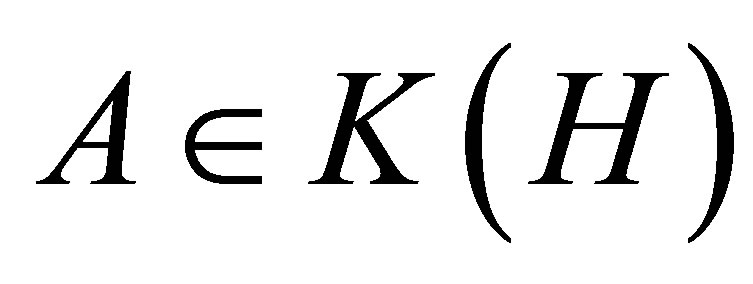 be normal operator, where
be normal operator, where  is the Cartesian decomposition of
is the Cartesian decomposition of
 . Then
. Then
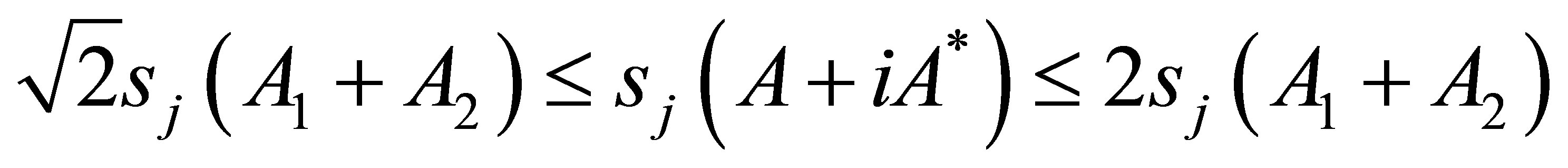

Proof. Note that  is normal operator, so we can write the Cartesian decomposition of
is normal operator, so we can write the Cartesian decomposition of  as
as
 where
where , and
, and
 where the cartesian decomposition of
where the cartesian decomposition of  is given by
is given by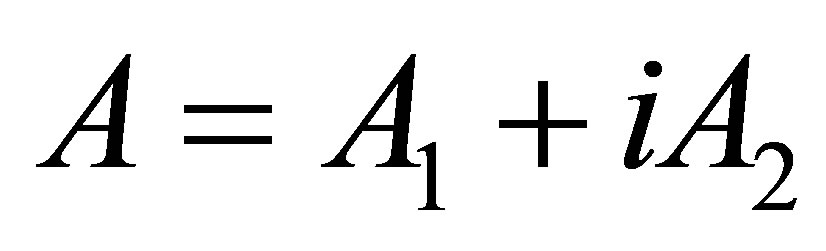 . By making comparison of
. By making comparison of  and
and  we see easily that
we see easily that . It follows that
. It follows that  . Moreover,
. Moreover,

Similarly, . Now, apply Theorem 2.2 to get
. Now, apply Theorem 2.2 to get
 (2.7)
(2.7)
 This is equivalent to saying that
This is equivalent to saying that

We will give simple and new proof to the inequality
(1.2).
Theorem 2.4. Let  such that
such that  is self-adjoint,
is self-adjoint,  , then
, then
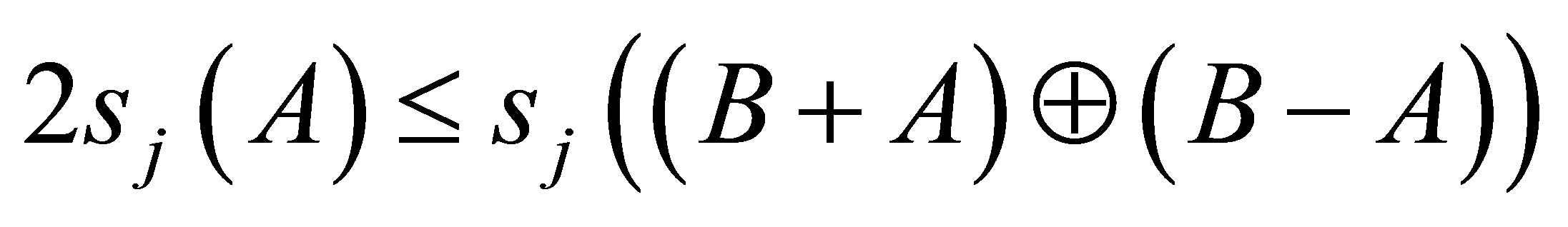

Proof. Since  is self-adjoint operator, we can write
is self-adjoint operator, we can write
 in the form
in the form  apply the inequality (1.4) we get
apply the inequality (1.4) we get
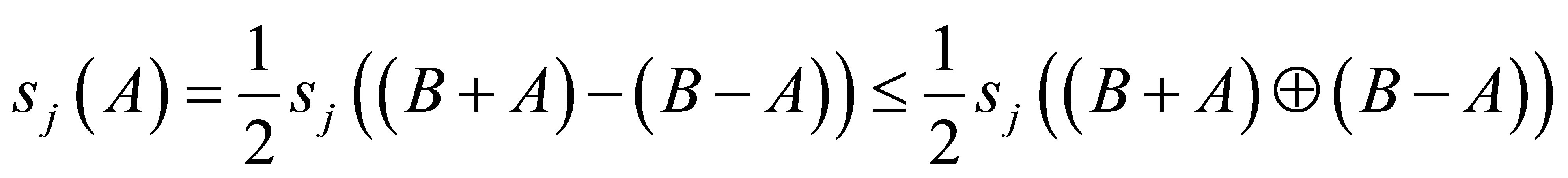
which is equivalent to saying that


Audeh and Kittaneh separates Jordan of self-adjoint operator in the inequality (1.3). Here we will give a shorter proof.
Theorem 2.5. Let  be self-adjoint operators. Then
be self-adjoint operators. Then
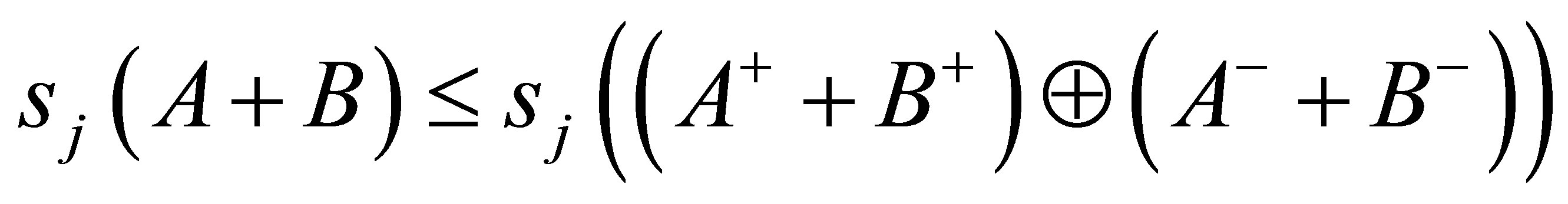

Proof. Since  and
and  are self-adjoint operators, we can write
are self-adjoint operators, we can write  in the form
in the form 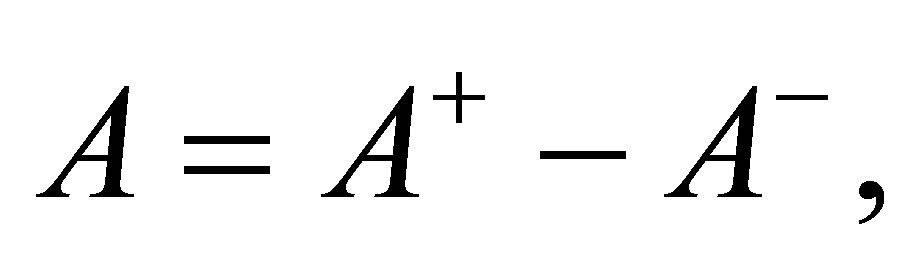 and similarly we will write
and similarly we will write  in the form
in the form . Apply the inequality (1.4) we get
. Apply the inequality (1.4) we get
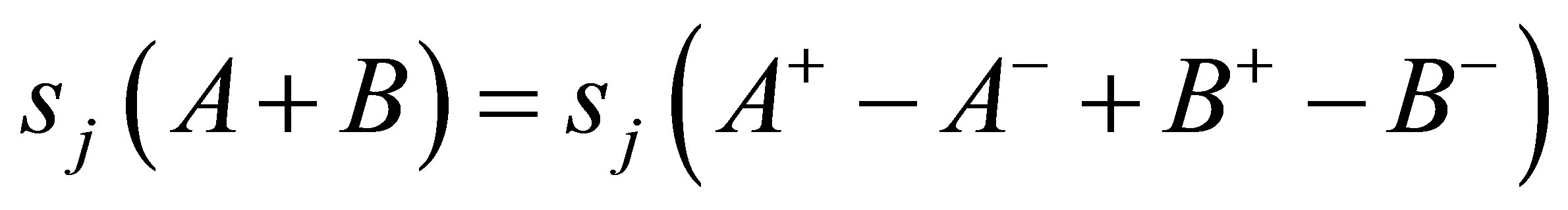
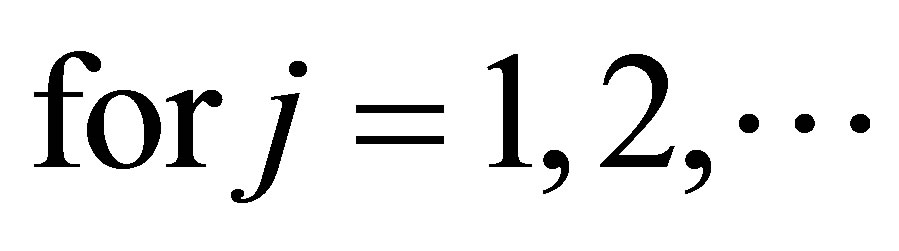
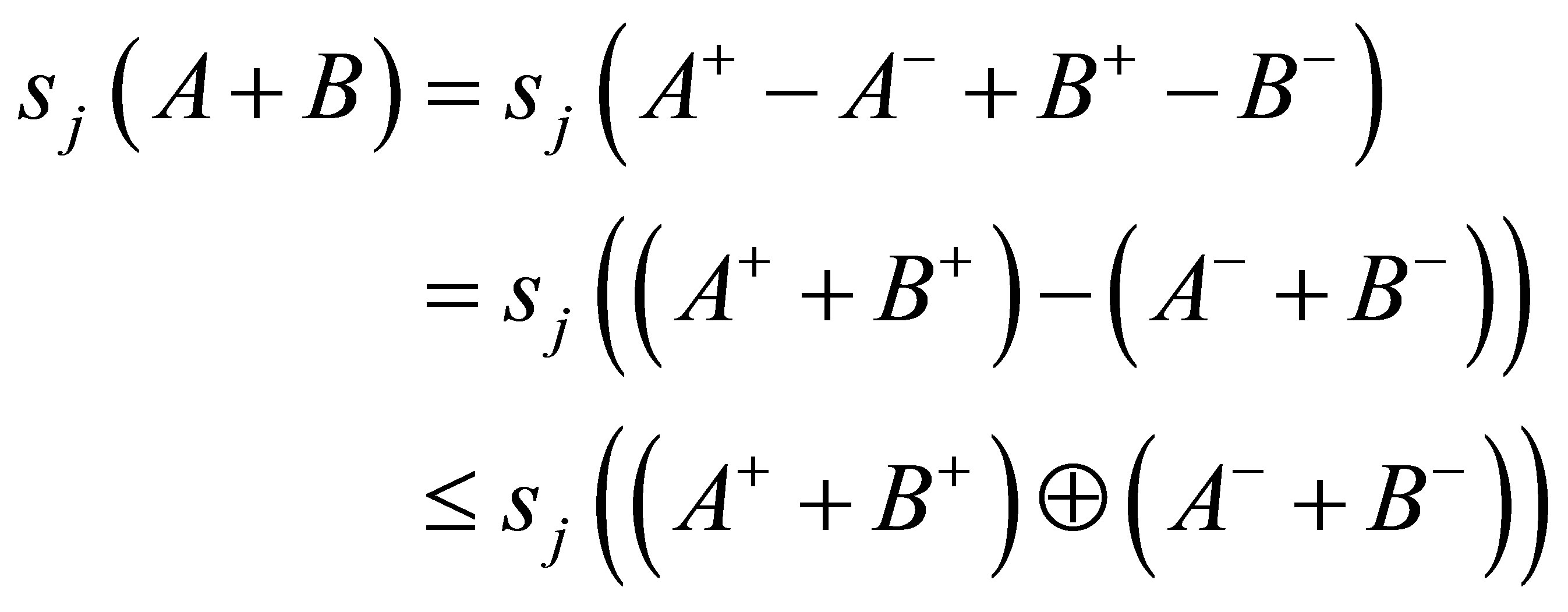
We will present the following two theorems as an application to the inequality (1.5).
Theorem 2.6. Let  be self-adjoint operator. Then
be self-adjoint operator. Then
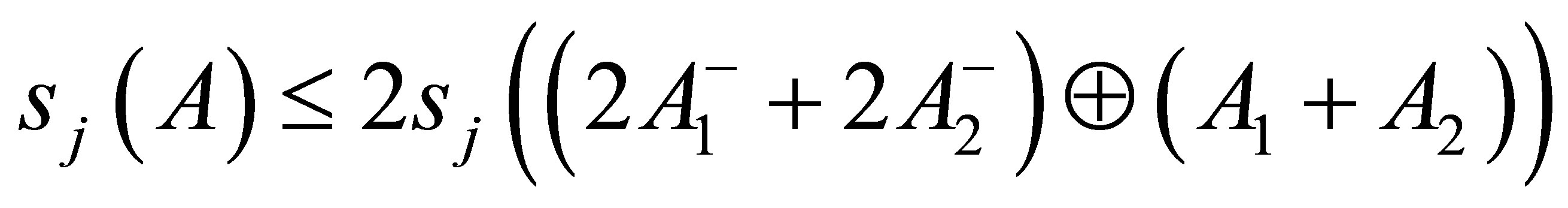 (2.8)
(2.8)
Proof. It was proved in Theorem 2.2 that if  is normal operator with Cartesian decomposition
is normal operator with Cartesian decomposition  , then
, then 
 from this, it follows that
from this, it follows that
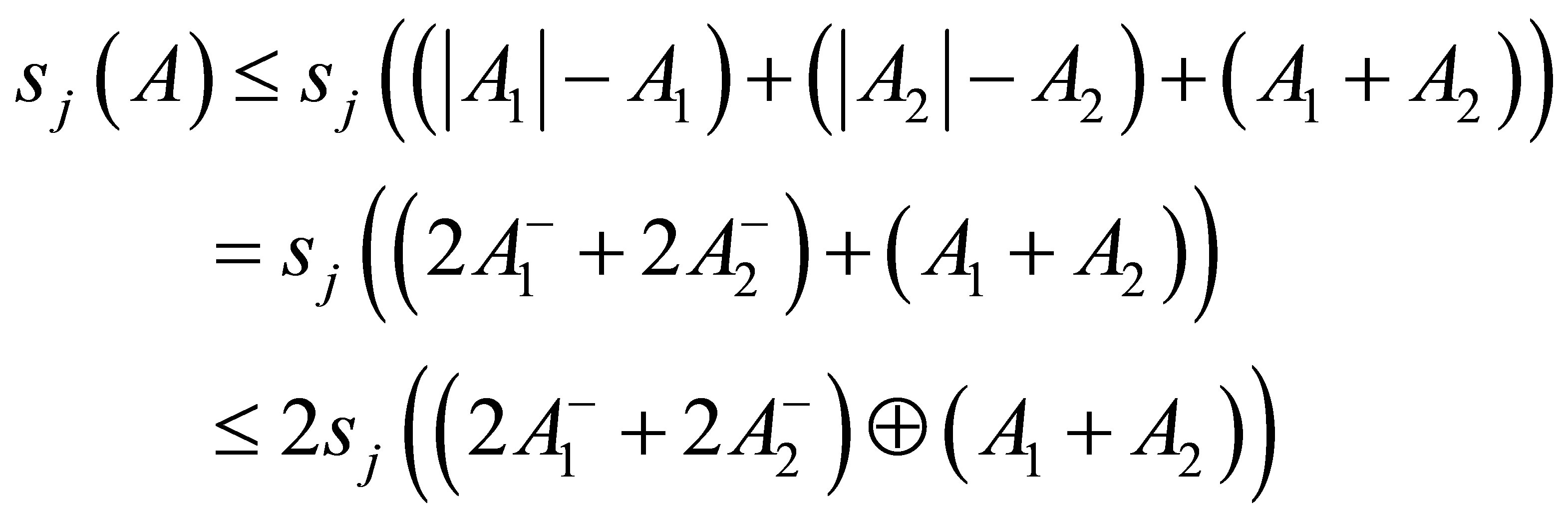
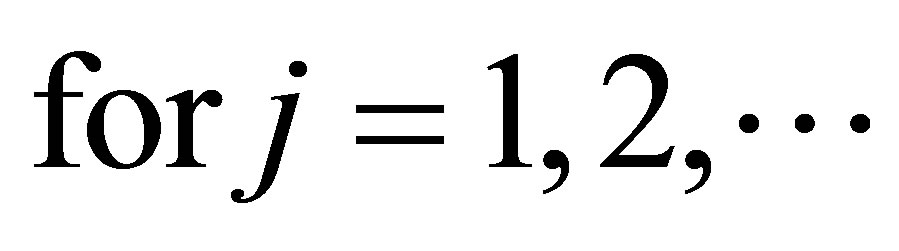
The following theorem is the second application of the inequality (1.5).
Theorem 2.7. Let  be self-adjoint operator. Then
be self-adjoint operator. Then
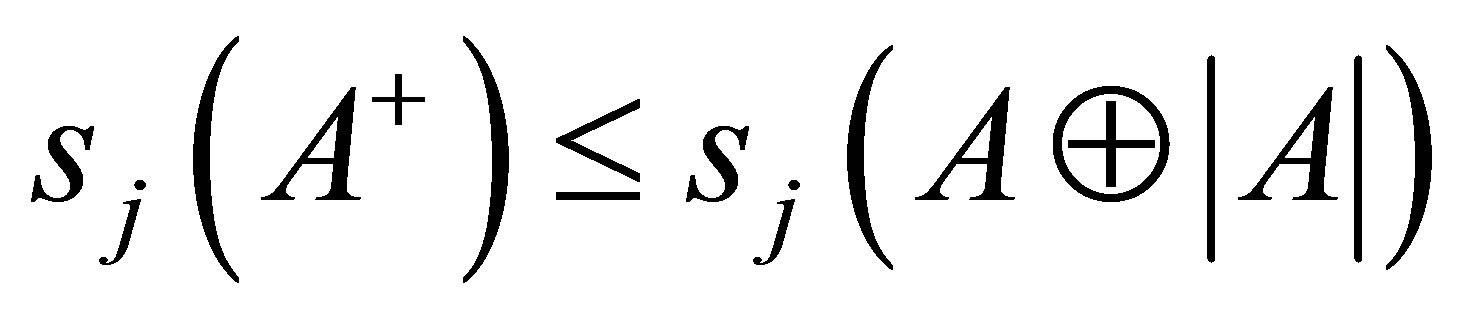 (2.9)
(2.9)
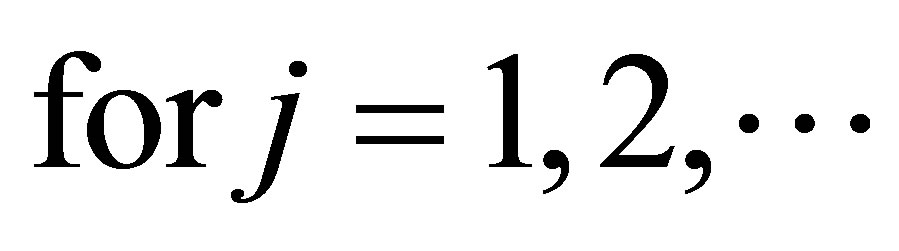 Moreover,
Moreover,
 (2.10)
(2.10)
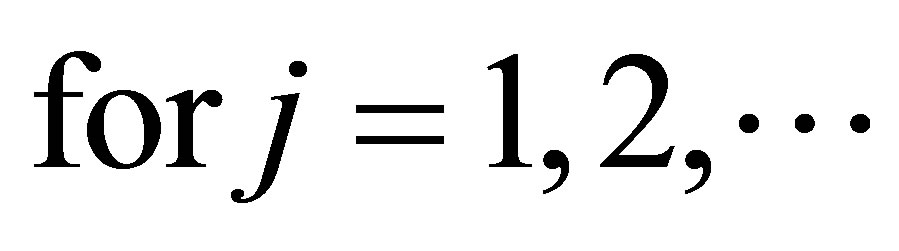
Proof. It is well known that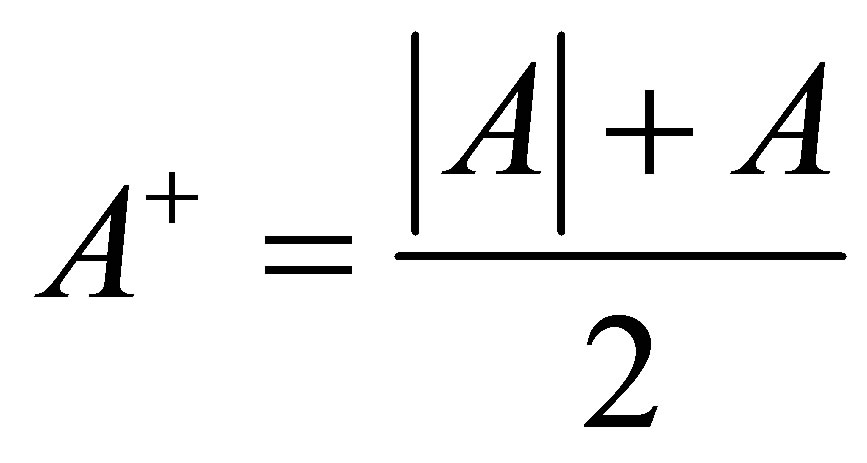 , so using the inequality (1.5) we get
, so using the inequality (1.5) we get
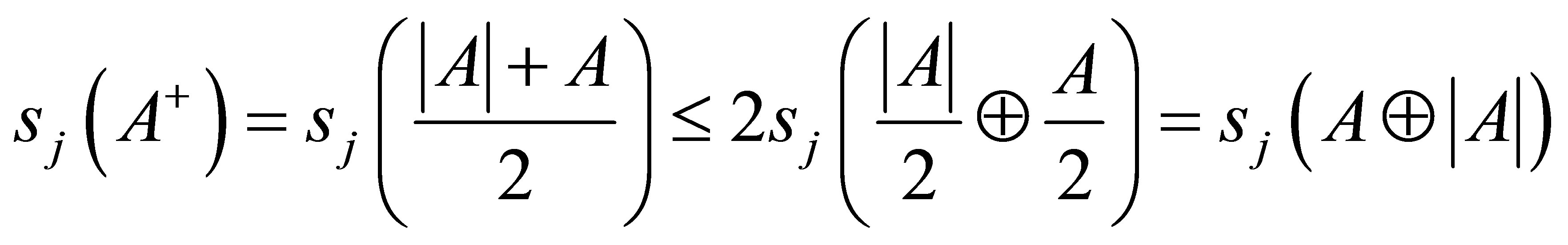

Similarly,  so using the inequality (1.5) we get
so using the inequality (1.5) we get

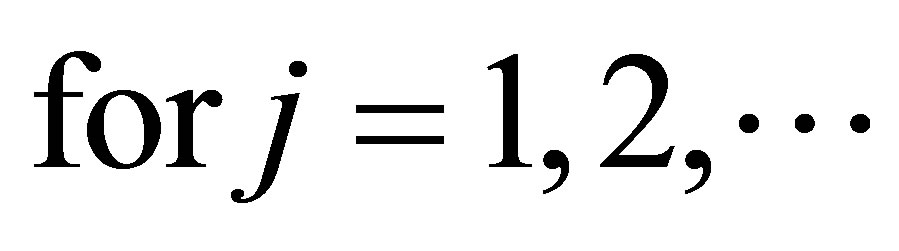
Bhatia and Kittaneh have proved in [6] that if , then
, then
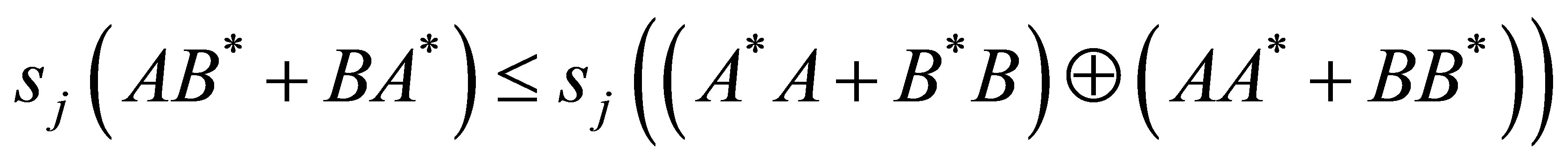
 For related Cauchy-Schwarz type inequalities, we refer to [2] and references therein. Here, we will present similar new inequality.
For related Cauchy-Schwarz type inequalities, we refer to [2] and references therein. Here, we will present similar new inequality.
Theorem 2.8. Let 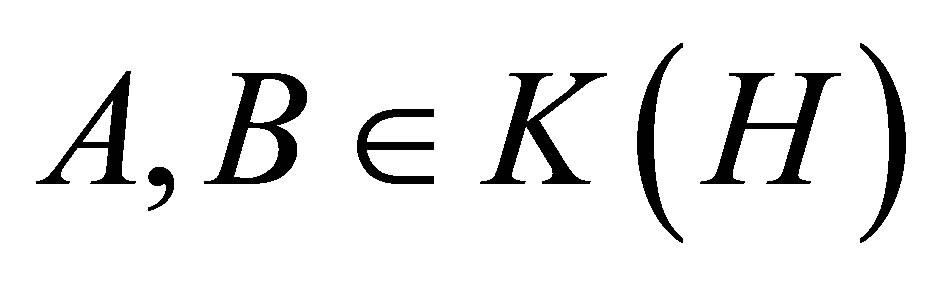 be operators. Then
be operators. Then
 (2.11)
(2.11)
Proof. Suppose  and
and  This implies that
This implies that
 , and
, and 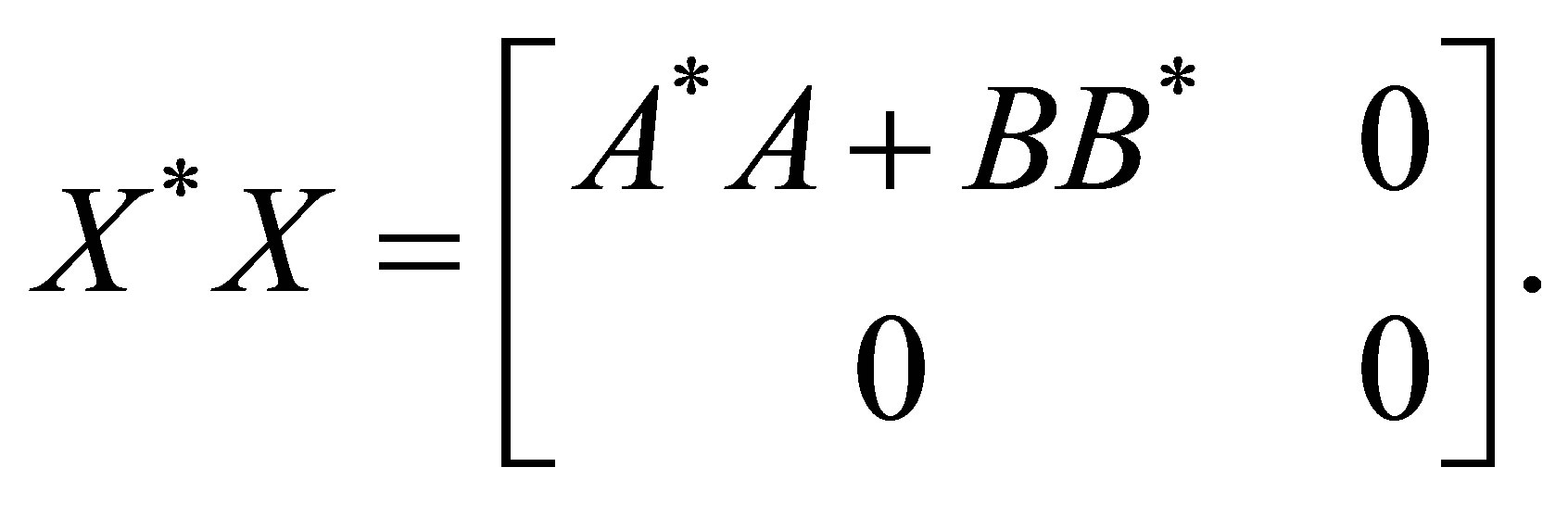
On the other hand, we have
 , and
, and .
.
Since 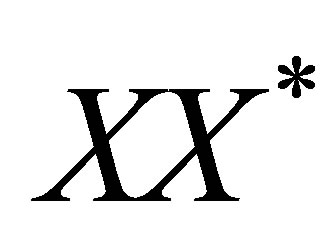 and
and  are positive operators, then
are positive operators, then
 is positive operator. Now by applying the inequality (1.1), we get
is positive operator. Now by applying the inequality (1.1), we get