On the Application of Bootstrap Method to Stationary Time Series Process ()
1. Introduction
The heart of the bootstrap is not simply computer simulation, and bootstrapping is not perfectly synonymous with Monte Carlo. Bootstrap method relies on using an original sample or some part of it, such as residuals as an artificial population from which to randomly resampled [1]. Bootstrap resampling methods have emerged as powerful tools for constructing inferential procedures in modern statistical data analysis. The Bootstrap approach, as initiated by [2], avoids having to derive formulas via different analytical arguments by taking advantage of fast computers. The bootstrap methods have and will continue to have a profound influence throughout science, as the availability of fast, inexpensive computing has enhanced our abilities to make valid statistical inferences about the world without the need for using unrealistic or unverifiable assumptions [3].
An excellent introduction to the bootstrap maybe found in the work of [4-9]. Recently, [10,11] have independently introduced non-parametric versions of the bootstrap that are applicable to weakly dependent stationary observations. Their sampling procedure have been generalized by [12,13] and by [14] by resampling “blocks of blocks” of observations to the stationary time series process.
In this article, we introduce a new resampling method as an improvement on the stationary bootstrap of [15] and the moving block bootstrap of [16,17].
The stationary bootstrap is essentially a weighted average of the moving blocks bootstrap distributions or estimates of standard error, where the weights are determined by a geometric distribution. The difficult aspect of applying these methods is how to choose b in moving blocks scheme and how to choose p in the stationary scheme.
On this note we propose a stationary bootstrap method generated by resampling blocks of random size, where the length of each block has a “truncated geometric distribution”.
In Section 2, the actual construction of a truncated geometric bootstrap method is presented. Some theoretical properties of the method are investigated in Section 3 in the case of the mean. In Section 4, it is shown how the theory may be extended to stationary time series processes.
2. Material and Method
To overcome the difficulties of moving blocks and geometric stationary scheme in determining both b (number of blocks) and p (probabilities). We introduced a truncated form for the geometric distribution and then demonstrated that it is a suitable model for a probability problem. This truncation is of more than just theoretical interest as a number of application has been reported [18,19].
A random length L may be defined to have a truncated geometric distribution with parameter P and N terms, when it has the probability distribution or probability density function
(2.1)
The constant K is found, using the condition
, to be 
Thus, we have
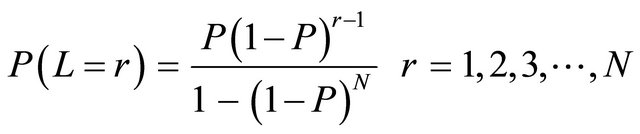(2.2)
These are the probabilities of a truncated geometric distribution with parameter P and N terms. Suppose that L length, number 1 to N are to be selected randomly with replacement. Then, the process continues until it is truncated geometrically at r with an appropriate probability P attached to its random selection in form of
,
. We take our N to be 4, that is, the random selections could be truncated between 1 to 4 at an appropriate probabilities.
Then, a description of the resampling algorithm when r > 1 is as follows:
1) Let 
be a random variables.
2) Let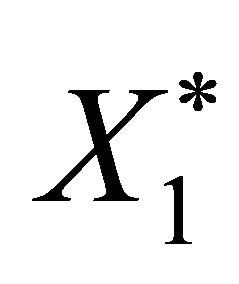 
be determined by the r-th truncated observation Xr in the original time series.
3) Let 
be equal to Xr+1 with probability 1 – P and picked at random from the original N observations with probability p.
4) Let
, be the block consisting of b observation starting from Xi.
5) Let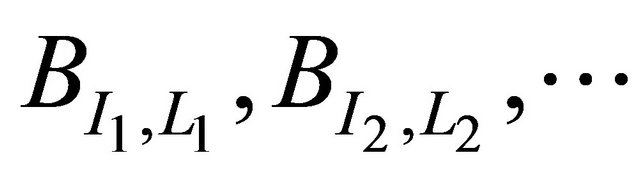 
be a sequence of blocks of random length determined by truncated geometric distribution.
6) The first L1, observations in the pseudo time series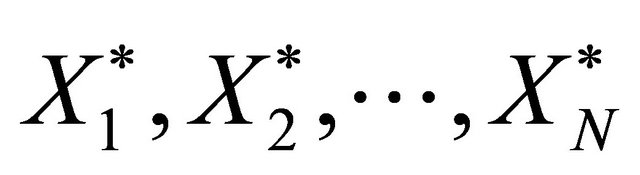 
are determined by the first block
, of observation 
the next L2 observations in the pseudo time series are the observations in the second sampled block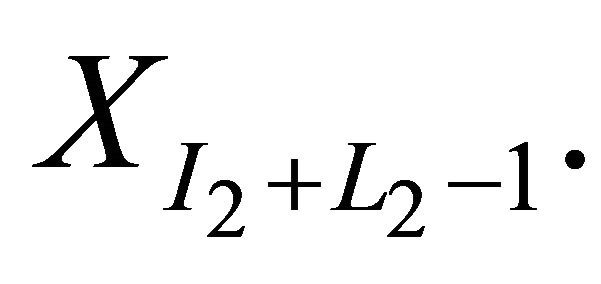
.
7) The process is resampled with replacement, until the process is stopped once N observation in the pseudo time series have been generated.
8) Once 
has been generated, one can compute the quantities of interest for the pseudo time series.
The algorithm has two major components, the construction of a bootstrap sample and the computation of statistics on this bootstrap sample, and repeat these operation many times through some kinds of a loop.
Proposition 1. Conditional on
, 
is stationary.
If the original observations 
are all distinct, then the new series 
is, conditional on
, 
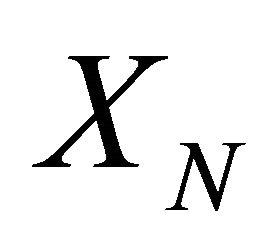a stationary Markov chain. If, on the other hand, two of the original observations are identical and the remaining are distinct, then the new series 
is a stationary second order Markov chain. The stationary bootstrap resampling scheme proposed here is distinct from the proposed by [20] but posses the same properties with that proposed by [21].
3. Result and Discussion
In this section, the emphasis is on the construction of valid inferential procedures for stationary time series data, and some illustrations with real data are given. The real data are the geological data from demonstratigraphic data from Batan well at 30 m regular interval, [22]. The data is the principal oxide of sand or sandstone, which is SiO2 or silicon oxide. The point is that the bulk of oil reservoir rocks in Nigeria sedimentary basins is sandstone and shale, a product of sill stone [23]. In other to improve on the geological analysis and prediction of the presence of these elements, a mathematical tool which can be used to examine a wide range of data sets is developed to detect and improve new and old oil basins.
The geological data of 130 observations was subjected to our new method described in section two of this article at 500 and 1000 bootstrap replicates, for block of (1, 2, 3, and 4).
The replicates with minimum variance was selected in each case of number of bootstrap replicates.
3.1. Model Fitting, Normality Test and Forecasting
The linear models are fitted and consider the choice of the order of the linear model on the basis of Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) and residual variance
, [24].
Fitting of AR Models to Bootstrapped Data
The linear models were fitted to the bootstrapped observations when the bootstrap replicates are (B = 500, B = 1000) for blocks of (1, 2, 3 and 4). When B = 500 replicates, we have the following models.
wang#title3_4:spBlock 1:
It is found that AIC and BIC is minzimum at P = 4.
The fitted model is
(3.1)
Block 2:
The fitted model is:
(3.2)
wang#title3_4:spBlock 3:
The model fitted is:
(3.3)
wang#title3_4:spBlock 4:
The fitted model is:
(3.4)
The table below shows the value of
, AIC and BIC for blocks (sizes) when B = 500 replicates.
When B = 1000 replicates
wang#title3_4:spBlock 1:
The fitted model is:
(3.5)
Block 2:
(3.6)
wang#title3_4:spBlock 3:
The fitted model is:
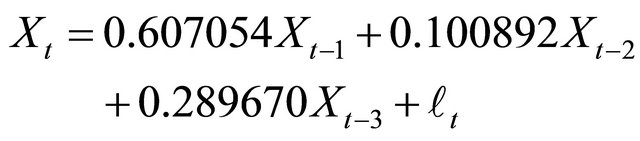(3.7)
wang#title3_4:spBlock 4:
The fitted model is:
(3.8)
The table below summarizes the value of
, AIC and BIC for blocks (sizes) when B = 1000 replicates.
From Tables 1 and 2, it observed that the residual variance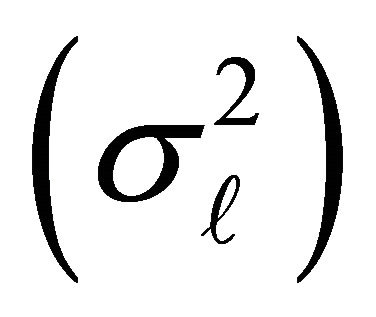 
for each block sizes are moderate, indicating a selection procedure from any of the models retain the time series data structure and any prediction from it is reliable.
3.2. Normality Test for Residual of Fitted Models
An important assumption we have made in fitting the linear and non-linear models to data is that the error 
of the model are mutually independent and normal. If a model is fitted to some data it may be appropriate to see whether the assumption is satisfied. Once it is satisfied
Table 1. Measure of goodness fit by block sizes for 500 replicates.
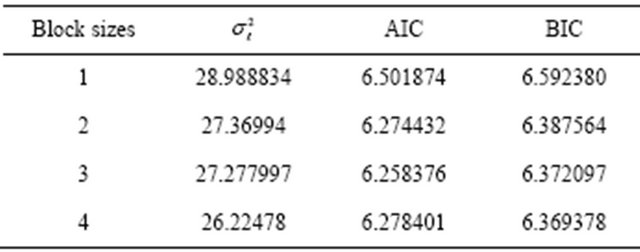
Table 2. Measures of goodness of fit by block sizes for 1000 replicates.
one can consider the model suitable for forecasting.
The normality test for residuals of fitted models is carried out using Jargue-Bera statistic tests (JB). At 5% level of significance with 2 degree of freedom the critical values of 
is 5.99, (15) So, if JB > 5.99, one rejects the null hypothesis that the test is normal.
Test for AR models of 500 replicates
H0: The test is normal H1: The test is not normal
Table 3 reveals that the test is normal in all the block sizes.
Test for AR models of 1000 replicates
H0: The test is normal H1: The test is not normal
Table 4 reveals that the test is normal in all block sizes.
Therefore, the normality test carried out in this article reveals that the proposed truncated geometric bootstrap method for dependent data at different replications is normal in all block sizes and any forecast from this models are good. That is, the residual of the models satisfied the normality test.
3.3. Forecasting
The linear models are fitted and then prediction or forecast are calculated for the next 10 observations. The following are the forecast values for 500 and 1000 replicates of different block sizes.
The forecast values for the replication of different block sizes from the Tables 5 and 6 reveals that while the probability forecast increases that of elementary forecast are not stable over time. The forecast shows a decline values throughout the period, except for block of
Table 3. Summary for JB statistics, B = 500.
Table 4. Summary for JB statistics, B = 1000.
Table 5. Forecast values for B = 500 replicates.
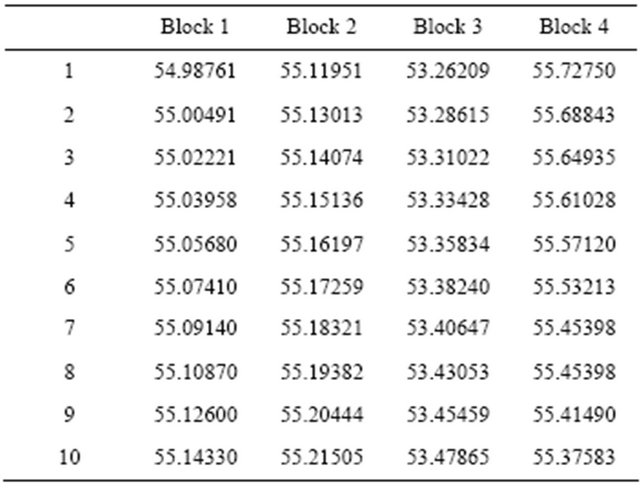
Table 6. Forecast values for B = 1000 replicates.
Table 7. Root mean square error
, for the forecast value.
3, that shows upward values throughout the period.
In order to justify the best model for prediction, one must consider the root mean square error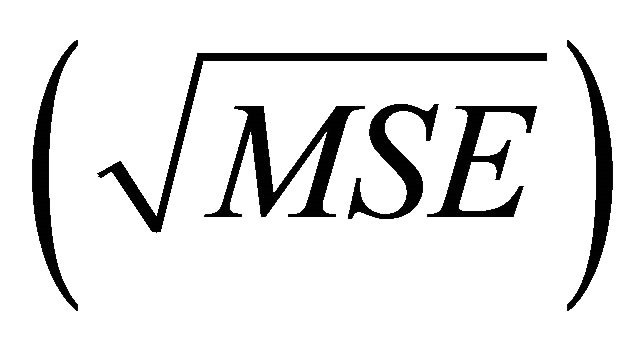 
of the forecast values. Table 7 is some of root mean square error of the forecast values.
To measure and establish the best model, we use the root mean square error of the forecast values. The above table reveals that the values are moderate for all the models in all bootstrap replicates. Therefore models fitted for all block of sample sizes are the best model for prediction purposes.
4. Summary and Conclusions
The truncated geometric bootstrap method proposed in this article is able to determine P in (0, 1) and provides b, for stationary time series process.
We proposed an algorithm for effective truncated geometric bootstrap method, which shares the construction of resampling blocks of different sizes of observation to form pseudo-time series, so that the statistics of interest are calculated along based on the resampled data sets. We implemented this method with real geological data and generated bootstrap replications of (B = 500 and 1000) for different block sizes of (b = 1, 2, 3, 4) which represents each number of truncations.
The linear models of AR (10) are fitted to the resampled pseudo-time series data, and the choice of the order are determined by AIC and BIC. The normality test was carried out using Jargue Bera statistic on the residual variance of the fitted models. Forecast was generated for the next 10 observations based on the fitted models, which are justified by root mean square error of the models.
In conclusion, the bootstrap method gives a better and a reliable models for predictive purposes. All the models for the different block sizes are good. They preserve and maintain stationary data structure of the process and are reliable for predictive purposes, confirming the efficiency of the proposed method.