High-Frequency Electrostatic SW at the Boundary between Quantum Plasma and Metal ()
1. Introduction
Recently, there has been a great deal of interest in investigating quantum plasma which is characterized by high plasma particle densities and low-temperature, in contrast to classical plasma which has high-temperatures and low particle number densities. Quantum plasmas are common in different environments, e.g. in superdense astrophysical bodies [1] (i.e. the interior of Jupiter and massive white dwarfs magnetors, and neutron stars), in intense laser-solid density plasma experiments [2-4], and in ultra-small electronic devices [5], quantum dots, nanowires [6], carbon nanotubes [7], quantum diodes [8], biophotonics [9], ultra-cold plasmas [10] and microplasmas [11].
Besides, quantum plasmas are gaining momentum [12] in the context of studies of waves, instabilities and nonlinear structures. The quantum effects become important in plasmas when de Broglie wavelength associated with the particles is equal to or greater than the average interparticle distance.
Quite recently, Glenzer et al. [13] have experimentally confirmed the collective X-ray scattering of plasmons in solid-density plasmas. It has been also demonstrated [14] that the bulk (high frequency) electronstatic oscillations can propagate in an underdense quantum plasma due to the quantum mechanical effects (the Bohm potential). Lazer et al. [15] has presented the dispersion relation for surface plasmons that can exist on a dense quantum plasma half-space. Also, Mohamed [16] studied the quantum effects on the propagation of electromagnetic surface waves in magnetized and unmagnetized plasma and got the dispersion relations for TM- (and TE- [17]) polarized surface modes.
In this letter, it has been studied the possibility of propagation of electrostatic surface waves on the boundary between a metal and quantum plasma by employing the full set of the quantum hydrodynamic model (QHD). Besides, the effect of external magnetic field is also taken into account.
2. Modeling Equations
Let the half-space  be filled by a gaseous (or semiconducting plasma with a finite thermal electron pressure, we assumed that ions are cold and the electrons obey the equation of state pertaining to a one-dimensional zero-temperature Fermi gas [18] as:
be filled by a gaseous (or semiconducting plasma with a finite thermal electron pressure, we assumed that ions are cold and the electrons obey the equation of state pertaining to a one-dimensional zero-temperature Fermi gas [18] as:
 (1)
(1)
where 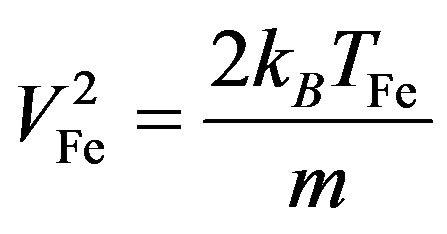 is the Fermi thermal speed,
is the Fermi thermal speed,  is the particle Fermi temperature, KB is the Boltizmann’s constant and
is the particle Fermi temperature, KB is the Boltizmann’s constant and  is the equilibrium particle density. In the x = 0 plane, the plasma is bounded by a perfectly conducting metal surface. However, Equation (1) is relevant to the physics of ordinary metal clusters and nanoparticles, for which the electron Fermi temperature is generally much higher than the room temperature [19].
is the equilibrium particle density. In the x = 0 plane, the plasma is bounded by a perfectly conducting metal surface. However, Equation (1) is relevant to the physics of ordinary metal clusters and nanoparticles, for which the electron Fermi temperature is generally much higher than the room temperature [19].
We consider electrostatic surface wave perturbations propagating transverse to the external magnetic field . We choose the potential depends on y-coordinate and the time in the form
. We choose the potential depends on y-coordinate and the time in the form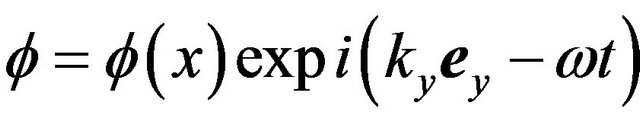 . We assume that the frequency of the waves studied is large compare to the characteristic ion frequency in the gaseous plasma (and the frequencies of the hole and phenon oscillations in the case of semiconductor plasma). The dynamics of the electrons are governed by the basic set of QHD equations:
. We assume that the frequency of the waves studied is large compare to the characteristic ion frequency in the gaseous plasma (and the frequencies of the hole and phenon oscillations in the case of semiconductor plasma). The dynamics of the electrons are governed by the basic set of QHD equations:
 (2)
(2)
 (3)
(3)
And the Poisson equation
 (4)
(4)
with 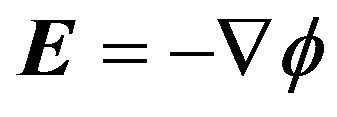 (here
(here  is the electrostatic potential). The quantum effects are represented by the momentum statistical effect involving the electron Fermi temperature
is the electrostatic potential). The quantum effects are represented by the momentum statistical effect involving the electron Fermi temperature  and
and  -dependent term which is called the Bohm potential term.
-dependent term which is called the Bohm potential term.
From perturbation theory and by expansion Equations (2) and (3), we can obtain the following equation:
 (5)
(5)
where


Besides, Equation (4) gives the following wave equation:
 (6)
(6)
Where  and
and  are the electron plasma frequency and cyclotron frequency. Equation (6) has the following finite solution for the perturbed density of the electron as:
are the electron plasma frequency and cyclotron frequency. Equation (6) has the following finite solution for the perturbed density of the electron as:
 (7)
(7)
where, C is the amplitude of the perturbed density and the very slow nonlocal variations are neglected (i.e.,  ). The wave Equation (5) for the potential of the surface waves has the following solution (as a function of the x-coordinate) in the two regions:
). The wave Equation (5) for the potential of the surface waves has the following solution (as a function of the x-coordinate) in the two regions:
 for
for  (8)
(8)
 for
for  (9)
(9)
where, D1 and D2 are the electrostatic potential of surface waves. One can show that the electrostatic potential is sharply increased at  with the following dispersion relation:
with the following dispersion relation:
 (10)
(10)
For the boundary conditions which consist in the vanishing of the potential and the normal component of the hydrodynamic electron velocity on the boundary of the metal with plasma, we get the amplitudes (D1 and D2) of the potential at the two regions.
 and
and 
Also, the general dispersion relation for the high-frequency electrostatic surface waves is obtained as follows:
 (11)
(11)
3. Discussions
In this section, we discuss and investigate the dispersion relationship (11) analytically and numerically in some cases. First, in the absence of the external magnetic field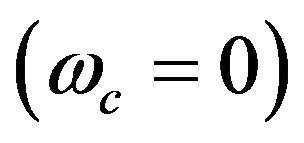 , it is reduced to the following equation:
, it is reduced to the following equation:
 (12)
(12)
In the case of cold  classical plasma (in contact with vacuum) Equation (12) gives the frequency of surface plasmons
classical plasma (in contact with vacuum) Equation (12) gives the frequency of surface plasmons .
.
By ignoring the effects caused by the Bohm potential , we have
, we have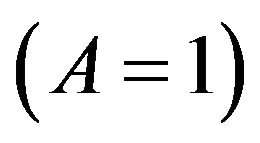 :
:
 (13)
(13)
which agrees with the equation derived by Lazar et al. [15] (at ) for the surface electrostatic waves on the plasma half-space.
) for the surface electrostatic waves on the plasma half-space.
Introducing the normalized quantities ,
, 
 and the plasmonic coupling
and the plasmonic coupling  which describes the ratio of plasmonic energy density to the electron Fermi energy density, we rewrite Equation (12):
which describes the ratio of plasmonic energy density to the electron Fermi energy density, we rewrite Equation (12):
 (14)
(14)
where .
.
For typical parameters of the gold metallic plasma at room temperature [15], n0 = 5.9 × 1022 cm−3, ωp = 1.37 × 1016 s−1, and , Equation (14) is plotted for different H.
, Equation (14) is plotted for different H.
It has been found that Equation (13) has two positive solutions ( and
and ) for different plasmonic coupling ratio H. Figure 1 displays the dispersion relation of electrostatic SW between unmagnetized quantum plasma and gold metal for different quantum ratios H = 0, 3 and 5. It is noticed for unmagnetized plasma that phase velocity of electrostatic SW increases with increasing quantum effects (the increase is more in the case of
) for different plasmonic coupling ratio H. Figure 1 displays the dispersion relation of electrostatic SW between unmagnetized quantum plasma and gold metal for different quantum ratios H = 0, 3 and 5. It is noticed for unmagnetized plasma that phase velocity of electrostatic SW increases with increasing quantum effects (the increase is more in the case of  than
than ).
).
The dispersion relation (11) of electrostatic SW in magnetized plasma is also putting in the form of normalized quantities as follows:
 (15)
(15)
Equation (15) is plotted for the previous parameters of the gold metallic plasma, where
 . It has been found in
. It has been found in
Figure 2 that phase velocity decreases with increased external magnetic field until cyclotron frequency equal plasma frequency 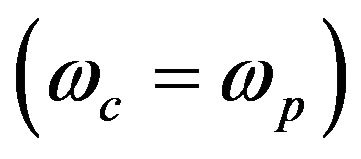 at which it decreases to zero for quantum plasmonic parameter H = 1. But with
at which it decreases to zero for quantum plasmonic parameter H = 1. But with

Figure 1. Dispersion relation of electrostatic SW in unmagnetized quantum plasma for different quantum ratios H = 0, 3 and 5 with frequency of surface plasmons 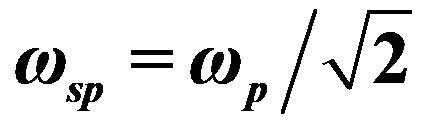 in case of cold (VFe ® 0) classical plasma.
in case of cold (VFe ® 0) classical plasma.
increasing the quantum parameter to H = 3 (Figure 3), the phase velocity tends sharply to zero nearly at 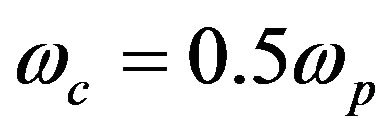 .
.
4. Conclusion
In this work, we have discussed the linear properties of the propagation of high frequency electrostatic surface waves on the boundary between metal and magnetized plasma based on the quantum hydrodynamic model. We have taken account of Fermi pressure and Bohm poten-

Figure 2. Dispersion relation of electrostatic SW between quantum plasma and gold metal with quantum plasmonic ratio H = 1 for different external magnetic fields ( = 0, 0.1, 0.5, 1) at which the phase velocity decreases with increased external magnetic field.
= 0, 0.1, 0.5, 1) at which the phase velocity decreases with increased external magnetic field.

Figure 3. Plot frequency and wave number of electrostatic SW along the external magnetic field with quantum plasmonic ratio H = 3. It shows that the phase velocity tends sharply to zero nearly at .
.
tial terms in our calculations. Also, the effect of strong external magnetic field which is parallel to the wave propagation has been investigated. We have derived the dispersion relations for these electrostatic SW modes in different cases (quantum or classical and magnetized or unmagnetized plasma). It is shown that the increasing of external magnetic field decreases the phase velocity to zero depending on quantum plasmonic ratio H. However, it has been investigated that for typical parameters of gold metallic plasma the quantum effects must be taken into account.