A Weaker Constraint Qualification of Globally Convergent Homotopy Method for a Multiobjective Programming Problem ()
1. Introduction
Let 
be the 
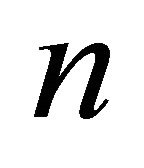-dimensional Euclidean space, and let 
and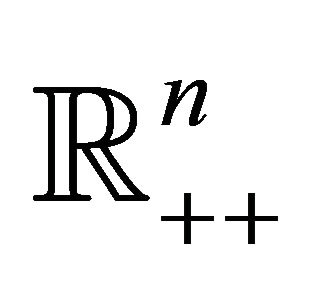 
denote the nonnegative and positive
, respectively. For any two vectors 
and 
in
, we use the following conventions: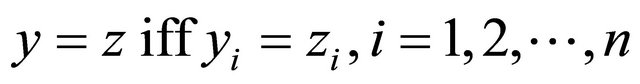
. Similarly, we can define
, and
.
Consider the following multiobjective programming problem (MOP)
where
We assume that all 
and 
are twice continuously differentiable functions, where 
Let
It is well known that if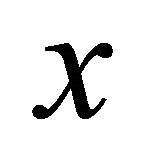 
is an efficient solution of (MOP), under some constraint qualifications, such as the Kuhn and Tucker constraint qualification (see Ref. [2]) or the Abadie constraint qualification (see Ref. [3]), then the following Karush-Kuhn-Tucker (KKT) condition at 
for (MOP) holds (see Refs. [4,5]):
(1)
where 
and
We say that 
is a KKT point of (MOP) if it satisfies the KKT condition.
Since the remarkable papers of Kellogg et al. (Ref. [6]) and Chow et al.(Ref. [7]) have been published, more and more attention has been paid to the homotopy method. As a globally convergent method, the homotopy method (or path-following method) now becomes an important tool for numerically solving nonlinear problems includeing nonlinear mathematical programming and complementarily problems (see Refs. [3,4]).
In 1988, Megiddo (see Ref. [8]) and Kojima et al. (see Ref. [9]) discovered that the Karmakar interior point method was a kind of path-following method for solving linear programming. Since then, the interior path-following method has been generalized to convex programming, and becomes one of the main methods for solving mathematical programming problems. Among most interior methods, one of the main ideas is numerically tracing the center path generated by the optimal solution set of the so-called logarithmic barrier function. Usually, the strict convexity of the logarithmic barrier function or nonemptiness and boundedness of the feasible set (see Ref. [10]) are needed. In 1997, Lin, Yu and Feng (see Ref. [11]) presented a new interior point method—combined homotopy interior point method (CHIP method)—for convex nonlinear programming without such assumptions. Subsequently, Lin, Li and Yu (see Ref. [12]) generalized CHIP method to general nonlinear programming where, instead of convexity condition, they used a more general “normal cone condition”.
In 2003, Lin, Zhu and Sheng (see Ref. [13]) generalized CHIP method to convex multiobjective programming(CMOP) with only inequality constraints. Instead of (CMOP), they considered an associated non-convex nonlinear scalar optimization problem and constructed the homotopy mapping.
In Refs. [1,14], we considered a combined homotopy interior point method for the multiobjective programming (MOP) under the condition linearly independent constraint qualification (LICQ). To find a KKT point of (MOP), we construct a homotopy as follows
(2)
where 
Let
Let 
be a nonempty closed set and
. We recall that the Fréchet normal cone of 
at 
is defined as
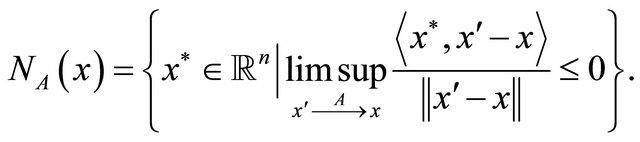
We used the following basic assumptions which are commonly used in that literature:
(A1) 
is nonempty (Slater condition) and bounded;
(A2) (LICQ) 
the matrix
is a matrix of full column rank;
(A3) Normal condition:
It is well known that if condition (A2) holds, then
(3)
We have proved the following convergence result in Ref. [1].
Theorem 1.1 (Convergence of the method) Suppose 
and 
are twice continuously differentiable functions such that the conditions (A1), (A2), and (A3) hold. Then for almost all
the zero-point set 
of the homotopy map (2)
contains a smooth curve 
which starts from 
As 
the limit set
of 
is nonempty, and the
component of every point in 
is a KKT point of (MOP).
Recently, many researchers extended and improved the results in Ref. [1] to convex multiobjective programming problem, see Ref. [14-17]. The purpose of this paper is to show that Theorem 1.1 remains true under the condition MFCQ instead of LICQ. The paper is organized as following. In Section 2, we prove the existence and convergence of a smooth homotopy path from almost any interior initial point 
to a solution of the KKT system of (MOP) under the condition MFCQ.
2. Main Results
We need the following elementary condition.
(A2′) (MFCQ) For every 
the following conditions hold:
• 
are linear independent;
• there exists a 
such that
and 
Clearly, condition (A2) implies (A2′). It is also known that if (A2′) holds, then (3) remains valid.
By using an analogue argument as in Ref. [1], we can prove the following two theorems.
Theorem 2.1 Suppose that 
and conditions (A1), (A2′) hold. Then for almost all initial points
is a regular value of 
and 
consists of some smooth curves. Among them, a smooth curve, say 
starts from 
Theorem 2.2 Suppose that 
and conditions (A1), (A2′) hold. For a given 
if 0 is a regular value of
, then the projection of the smooth curve 
on the 
component is bounded.
We next prove that 
is a bounded curve.
Theorem 2.3 (Boundedness) Suppose that the conditions (A1), (A2′), and (A3) hold. Then for a given
if 0 is a regular value of
, then 
is a bounded curve.
Proof: By Theorem 2.2, it is sufficient to show that the 
component of smooth curve is bounded. Suppose that there exists a sequence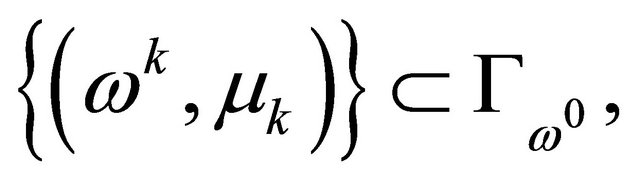 
such that
and
where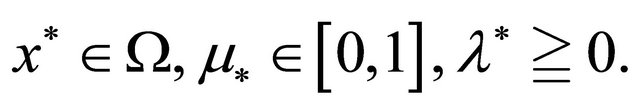 
Since closed unit circle of 
is compact, without loss of generality we can assume that
Clearly,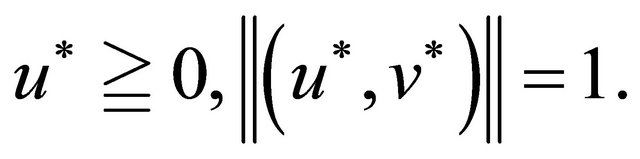 
By (2), we have
(4)
(5)
Let
By (5), we know 
Rewrite (4) as
(6)
Divide (6) by 
and let 
since
, (6) becomes
(7)
where
1) If 
then 
By
(A2′), 
This is a contradiction with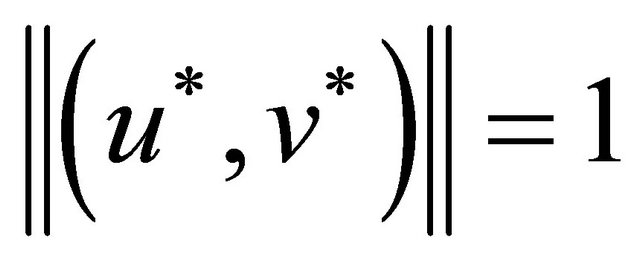
.
2) If 
we consider the following two cases:
1. If
, we know 
because of 
By (A2′), there exists a nonzero vector 
such that
(8)
This, together with (7), implies that 
which is a contradiction.
2. If
, by (7) and (A2′), we know 
So,
since 
Because of (5), 
Thus
Without loss of generality, we can assume that
Hence 
a) If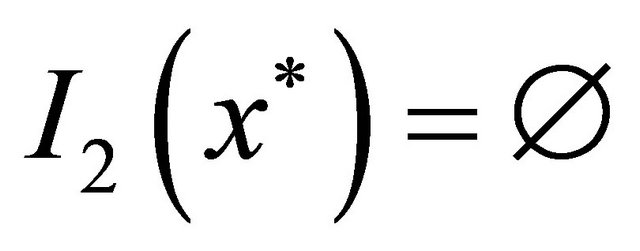
, then 
is bounded. We may assume 
Divide (6) by 
and let
(6) becomes
(9)
This implies that
exists. Indeed,
If
that is
By condition (A3),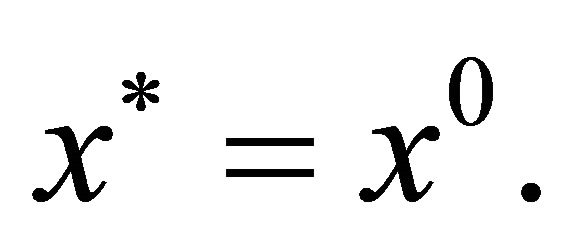 
This is impossible since
. So
By (9), we then have that 
exists. Assume 
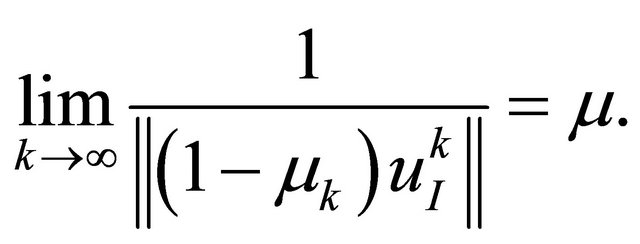
Then 
If
, (9) becomes
This contradicts to condition (A3).
If
, (9) becomes
By (A2′), there exists a nonzero vector 
such that
Thus 
which contradicts 
b) If
, without loss of generality, we can assume that
where 
Since
(10)
we divide (4) by 
and let 
we have that
(11)
If 
then
By condition (A2′), 
This is a contradiction since 
If 
by (A2′), there is a nonzero vector 
such that
This, together with (11), implies 
This is a contradiction.
Therefore, 
is a bounded curve.
By an analogue argument as in Ref. [1], it is easy to show the following result.
Theorem 2.4 (Convergence of the method) Suppose that the conditions (A1), (A2′), and (A3) hold. Then for almost all 
the zero-point set 
of the homotopy map (2) contains a smooth curve
which starts from 
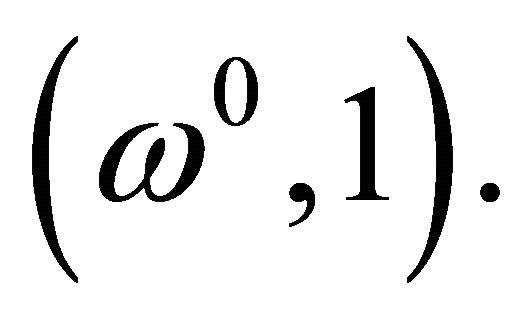As
the limit set 
of 
is nonempty, and every point in 
is a solution of (1).
Therefore, Theorem 2.4 shows that for almost all 
the homotopy Equation (2)
generates a smooth curve 
starts from 
which is called the homotopy path, the limit set
of 
is nonempty, and the x-component of every point in 
is a KKT point of (MOP), the 
of the homotopy path is the solution of (1) as 
goes to 0.