Spiky Development at the Interface in Rayleigh-Taylor Instability: Layzer Approximation with Second Harmonic ()
1. Introduction
Hydrodynamic instabilities such as Rayleigh Taylor instability (RTI) which sets in when a lighter fluid supports a heavier fluid against gravity or Richtmyer Meshkov instability (RMI) which is initiated when a shock passes an interface between two fluids with different acoustic impedances are of increasing importance in a wide range of physical phenomena starting from inertial confinement fusion (ICF) to astrophysical ones like supernova explosions. In ICF, the capsule shell undergoes the RTI both in the acceleration and deceleration phases. RTI can retard the formation of the hot spot by the cold RTI spike of capsule shell resulting in the destruction of the ignition hot spot or autoignition [1-4]. The hydrodynamic instabilities lead to development of heavy fluid “spikes” penetrating into the lighter fluid and “bubbles” of lighter fluid rising through the heavier fluid. Different approaches have been used for the study of such problems. Among these Layzer’s [5] approach applied to single mode potential flow model [6-11] is a useful one giving approximate estimate of both Rayleigh Taylor and Richtmyer Meshkov instability evolution. The bubbles were shown by Zhang [7] to rise at a rate tending asymptotically to a terminally constant velocity while spikes were shown to descend with a constant acceleration. However, whether for bubbles or for the spikes, Zhang’s analysis was applicable only for Atwood number A = 1, i.e., only for fluid-vacuum interface. An extension to arbitrary value of Atwood number A was done by Goncharov [8]. Within limitations of Layzer’s model as pointed out by Mikaelian [12] bubbles were shown to rise with a velocity tending to an asymptotic value dependent on A and having a fairly close agreement with the simulation results of Ramaprabhu et al. [13]. But the spikes were found to descend with a terminal constant velocity in contrast to a constant acceleration as obtained by Zhang [7] for A = 1.
Asymptotic spike evolution in Rayleigh Taylor instability behaving almost as a free fall was obtained by Clavin and Williams [14] and also by Duchemin et al. [15] by conformal mapping method. Associated with the free fall of the spike, the surface curvature of the spike was also found to increase with time (i.e. the spike sharpens as it falls).
The present paper described the dynamics of bubble and spike tips arising at the two fluid interfacial structure due to RTI with extended Layzer’s model replacing the zeroth harmonic term [8] by second harmonic term to satisfy the condition that the fluid velocity vanishes at infinity. The obtained asymptotic velocity of the bubble tip is slightly large compared to the classical value derived by Goncharov [8] and coincide when A = 1. Although the asymptotic curvature of the bubble tip remain unchanged. On the other hand, the curvature of the spike tip is an increasing function of time as well as Atwood number. As time increases, the tip of the spike is shown to become sharpen and falling nearly free fall.
This paper is organized in the following manner. In Section 2, we described the potential flow model with extended Layzer’s approach and derived the governing equations of the interfacial structure. The behavior of the bubble and spike tips are discussed analytically and numerically in Section 3 and finally we conclude the results in Section 5.
2. Basic Model and Governing Equation
In the single mode Layzer model with generalization [8] for arbitrary Atwood number the equation to the interface taken in X-Y plane as
 (1)
(1)
with ,
,  for bubble while
for bubble while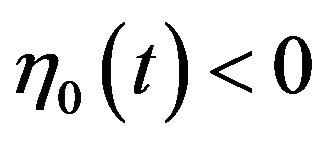 ,
,  for spike. The velocity potential describing the motion of the heavier fluid (density
for spike. The velocity potential describing the motion of the heavier fluid (density ) and the lighter fluid (density
) and the lighter fluid (density ) are (gravity g is along the negative y direction)
) are (gravity g is along the negative y direction)
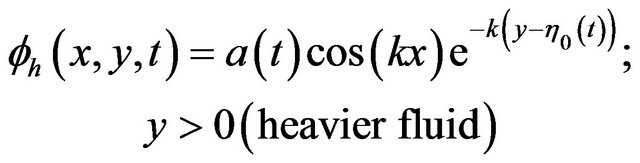 (2)
(2)
 (3)
(3)
where k is the wave number and ,
, 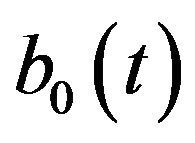 ,
,  are amplitudes. This conventional single mode Layzer model has the drawback that rather than conforming to the physical requirement:
are amplitudes. This conventional single mode Layzer model has the drawback that rather than conforming to the physical requirement:  as
as  it necessitates the assumption of a time dependent source at
it necessitates the assumption of a time dependent source at  [16]. To avoid this difficulty we modify the single mode Layzer model by replacing the zeroth mode term
[16]. To avoid this difficulty we modify the single mode Layzer model by replacing the zeroth mode term  in Equation (3) by a second harmonic term viz,
in Equation (3) by a second harmonic term viz,
 (4)
(4)
Equations (2) and (4) give
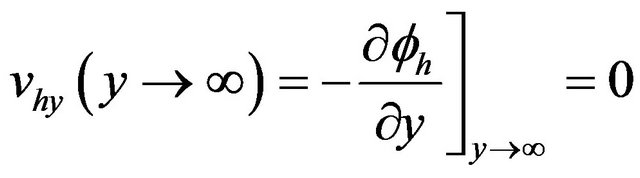 (5)
(5)
 (6)
(6)
The kinematic boundary conditions at the interface (1) are
 (7)
(7)
 (8)
(8)
Setting the pressure boundary condition  in Bernoulli’s equation for the heavier and lighter fluids leads to [7,8,11,17-22]
in Bernoulli’s equation for the heavier and lighter fluids leads to [7,8,11,17-22]
 (9)
(9)
Following the usual procedure [19-22], i.e., expanding  and the velocity potentials in powers of
and the velocity potentials in powers of 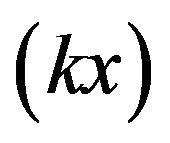 and equating coefficients of
and equating coefficients of ,
, 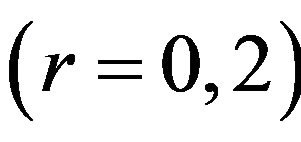 we obtain from Equations (7)-(9) the evolution equation for the RT bubbles/spikes (non-dimensionalized) tip elevation
we obtain from Equations (7)-(9) the evolution equation for the RT bubbles/spikes (non-dimensionalized) tip elevation  , curvature
, curvature  and velocity
and velocity 
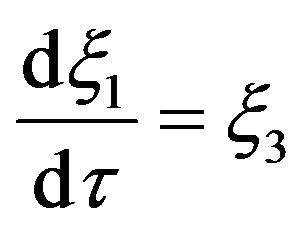 (10)
(10)
 (11)
(11)
 (12)
(12)
where
 (13)
(13)
and
 (14)
(14)
is nondimensionalized time.
3. Results and Discussion
Starting from a set of initial values ,
,  and
and  which correspond to the description of temporal evolution of the tip of the bubble we arrive at the asymptotic value
which correspond to the description of temporal evolution of the tip of the bubble we arrive at the asymptotic value 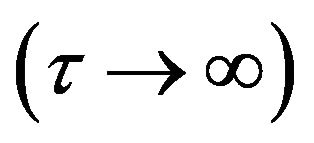
 (15)
(15)
and
 (16)
(16)
(by classical we mean the single mode Layzer approximation as used by Goncharov [8]). Two values coincide as . The growth rate of the development of the height of the bubble tip is shown in Figure 1 and compared with classical value. It is seen that presence or absence of a source does not give rise to any qualitatively significant change in the growth rate of the bubble height [8,9,17].
. The growth rate of the development of the height of the bubble tip is shown in Figure 1 and compared with classical value. It is seen that presence or absence of a source does not give rise to any qualitatively significant change in the growth rate of the bubble height [8,9,17].
To get spike like behavior of the perturbation of the interface we used
 (17)
(17)
Corresponding to a start from an initial value
 (18)
(18)
 (a)
(a) (b)
(b)
Figure 1. (a) Variation of ξ3 against A; and (b) Variation of ξ3 against τ, where the black line gives the saturation growth rate since by Equations (11) and (12) and the dashed line gives the classical value of growth rate of the tip of the bubble.
Equation (11) shows that  increases monotonically
increases monotonically
( for all
for all ) while from Equation (12) it follows that the depth of the spike tip below the surface of separation increases continuously (
) while from Equation (12) it follows that the depth of the spike tip below the surface of separation increases continuously ( and
and ). These are shown in Figures 2(a) and (b) by plotting
). These are shown in Figures 2(a) and (b) by plotting  and
and  as function of
as function of  obtained from numerical solution of Equations (11) and (12) by employing fifth order Runge-Kutta-Fehlberg method. The initial value taken are
obtained from numerical solution of Equations (11) and (12) by employing fifth order Runge-Kutta-Fehlberg method. The initial value taken are  and
and  −0.5 which satisfy condition (17) for all the following three values of
−0.5 which satisfy condition (17) for all the following three values of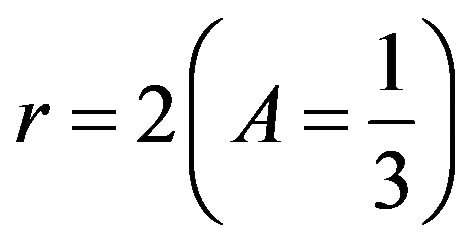 ,
,  ,
,
 . The value of
. The value of  which represents the curvature at the tip of the spike is an increasing function of
which represents the curvature at the tip of the spike is an increasing function of  for every value of the Atwood number A (Figure 2(a)). Moreover for every given value of
for every value of the Atwood number A (Figure 2(a)). Moreover for every given value of  the curvature
the curvature  increases with A. This implies that the spike continues to sharpen with time as well as with increasing
increases with A. This implies that the spike continues to sharpen with time as well as with increasing
 (a)
(a) (b)
(b)
Figure 2. (a) Variation of ξ2 against τ; and (b) Variation of ξ3 against τ with initial value ξ1 = −0.1, ξ2 = 1.0, ξ3 = −0.5 and r = 2 (dot-dashed), 5 (dashed), 20 (black).
Atwood number and is explicitly shown in Figure 3. Figure 2(b) shows that except very close to the starting instant the spike descends with a constant acceleration  (i.e., nearly a free fall). This agrees with the conclusions [7] for Atwood number A = 1.
(i.e., nearly a free fall). This agrees with the conclusions [7] for Atwood number A = 1.
The time development of spiky behavior for 
 and
and  is demonstrated in Figures 4(a) and (b). This is shown both for increasing A with fixed
is demonstrated in Figures 4(a) and (b). This is shown both for increasing A with fixed  (Figure 4(a)) and with increasing
(Figure 4(a)) and with increasing  for given A (Figure 4(b)). But for
for given A (Figure 4(b)). But for  with
with
 one encounters development of finite time singularity i.e.,
one encounters development of finite time singularity i.e.,  and
and  at a finite value of
at a finite value of . The possibility of the occurrence of such an eventuality at (or near) the tip of the spike is also found to arise when the RT instability is addressed by conformal mapping method [23,24] as mentioned by Clavin and Williams [14].
. The possibility of the occurrence of such an eventuality at (or near) the tip of the spike is also found to arise when the RT instability is addressed by conformal mapping method [23,24] as mentioned by Clavin and Williams [14].
Finally for a trajectory starting from  and
and
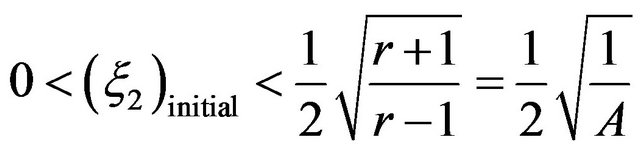 one finds that
one finds that  continues to increase towards
continues to increase towards , i.e., the spike continues to sharpen as time progresses and its speed of fall slowly decreases in magnitude. Because of the presence of singularity at
, i.e., the spike continues to sharpen as time progresses and its speed of fall slowly decreases in magnitude. Because of the presence of singularity at  (Equation (12)), it is not possible to continue the numerical integration towards and beyond this point. This is shown in Figure 5 for initial values in the domain mentioned above.
(Equation (12)), it is not possible to continue the numerical integration towards and beyond this point. This is shown in Figure 5 for initial values in the domain mentioned above.
4. Conclusion
In this report, we have extended the Layzer’s model with
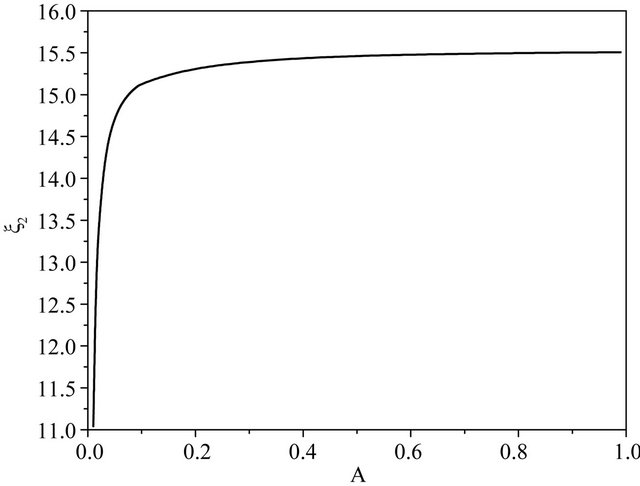
Figure 3. Variation of ξ2 against A with initial value ξ1 = −0.1, ξ2 = 1.0, ξ3 = −0.5.
the inclusion of second harmonic term. In asymptotic stage, the velocity of the tip of the bubble becomes
 which is slightly large compared to classical value and agree with the previous obtained results. However, in case of spike, the curvature of the spike tip is increasing with time as well as the Atwood number
which is slightly large compared to classical value and agree with the previous obtained results. However, in case of spike, the curvature of the spike tip is increasing with time as well as the Atwood number
 (a)
(a) (b)
(b)
Figure 5. (a) Variation of ξ2 against τ; and (b) Variation of ξ3 against τ with initial value ξ1 = −0.1, ξ2 = 0.1, ξ3 = −0.1 and r = 2 (dot-dashed), 5 (dashed), 20 (black).
and as time goes the spike becomes sharpen and behave like a free fall. This is a theoretical work supported by the other previous results.
5. Acknowledgements
This work is supported by the C.S.I.R, Government of India under ref. no. R-10/B/1/09.
NOTES