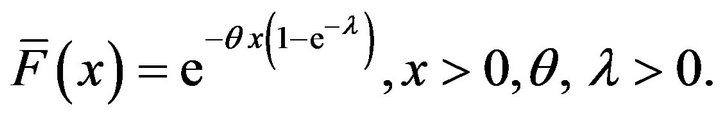On Moment Generating Function of Generalized Order Statistics from Erlang-Truncated Exponential Distribution ()
1. Introduction
A random variable X is said to have Erlang-truncated exponential distribution if its probability density function (pdf) is of the form
 (1)
(1)
and the corresponding distribution function  is
is
 (2)
(2)
where
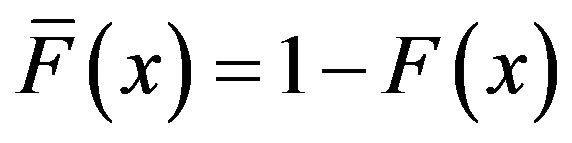 .
.
For more details on this distribution and its applications one may refer to [1].
[2] introduced and extensively studied the generalized order statistics . The order statistics, sequential order statistics, Stigler’s order statistics, record values are special cases of
. The order statistics, sequential order statistics, Stigler’s order statistics, record values are special cases of . Suppose
. Suppose 
 are n
are n  from an absolutely continuous distribution function
from an absolutely continuous distribution function 
 with the corresponding probability density function
with the corresponding probability density function 
 . Their joint pdf is
. Their joint pdf is
 (3)
(3)
for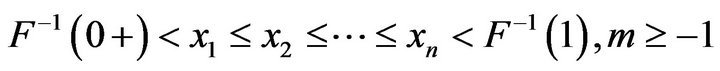 ,
,
 and
and  is a positive integer.
is a positive integer.
Choosing the parameters appropriately, models such as ordinary order statistics (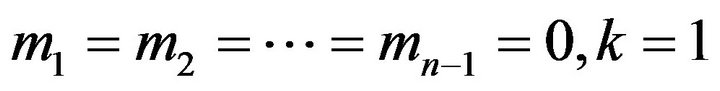
 ), k-th record values
), k-th record values
 , sequential order statistics
, sequential order statistics , order statistics with non-integral sample size
, order statistics with non-integral sample size
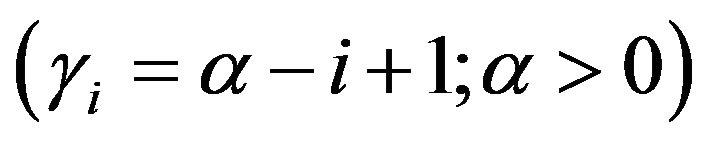 , Pfeifer’s record values
, Pfeifer’s record values
 and progressive type II censored order statistics
and progressive type II censored order statistics  are obtained [2, 3].
are obtained [2, 3].
The marginal 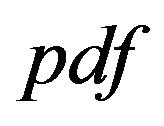 of the r-th
of the r-th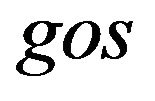 ,
,  ,
, 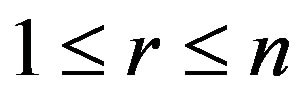 , is
, is
 (4)
(4)
and the joint  of
of  and
and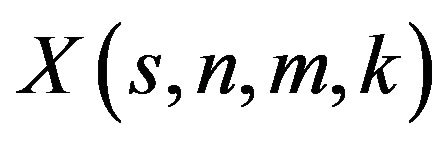 ,
,  , is
, is
 (5)
(5)
where
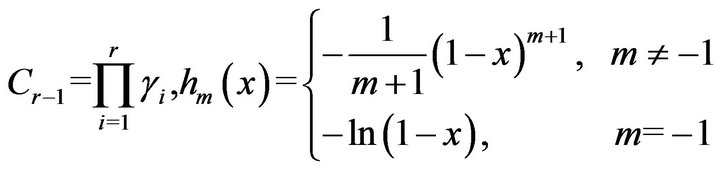
and .
.
[4-6] have established recurrence relations for moment generating functions of record values from Pareto and Gumble, power function and extreme value distributions.
Recurrence relations for marginal and joint moment generating functions of  from power function distribution are derived by [7]. [8,9] have established recurrence relations for conditional and joint moment generating functions of
from power function distribution are derived by [7]. [8,9] have established recurrence relations for conditional and joint moment generating functions of  based on mixed population, respectively. [10] has established explicit expressions and some recurrence relations for moment generating function of gos from Gompertz distribution.
based on mixed population, respectively. [10] has established explicit expressions and some recurrence relations for moment generating function of gos from Gompertz distribution.
In the present study, we establish exact expressions and some recurrence relations for marginal and joint moment generating functions of gos from Erlang-truncated exponential distribution. Results for order statistics and record values are deduced as special cases and a characterization of this distribution is obtained by using the conditional expectation of function of gos.
2. Relations for Marginal Moment Generating Functions
Note that for Erlang-truncated exponential distribution defined in (1).
 . (6)
. (6)
The relation in (6) will be exploited in this paper to derive exact expressions and some recurrence relations for the moment generating functions of  from the Erlang-truncated exponential distribution.
from the Erlang-truncated exponential distribution.
Let us denote the marginal moment generating functions of  by
by 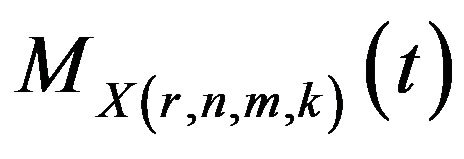 and its j-th derivative by
and its j-th derivative by .
.
We shall first establish the explicit expression for . Using (4) and (6), we have when
. Using (4) and (6), we have when 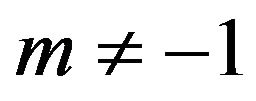
 , (7)
, (7)
where
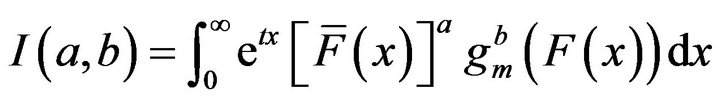 . (8)
. (8)
On expanding 
binomially in (8), we get when 
 , (9)
, (9)
where

On substituting for  from (2) in (9), we have
from (2) in (9), we have
 (10)
(10)
Now on substituting for  from (10) in (7) and simplifying, we obtain when
from (10) in (7) and simplifying, we obtain when 
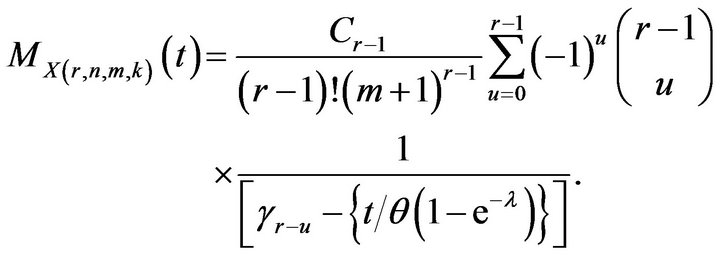 (11)
(11)
When , we have
, we have

Since (11) is of the form  at
at , therefore, we have
, therefore, we have
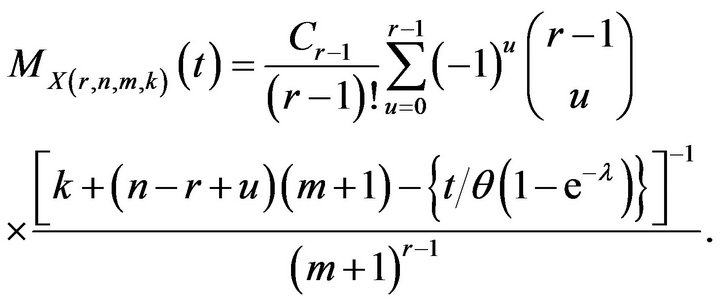 (12)
(12)
Differentiating numerator and denominator of (12)  times with respect to
times with respect to , we get
, we get

On applying L’ Hospital rule, we have
 (13)
(13)
But for all integers  and for all real numbers x, we have [11]
and for all real numbers x, we have [11]
 (14)
(14)
Therefore,
 (15)
(15)
Now on substituting (14) in (13), we find that
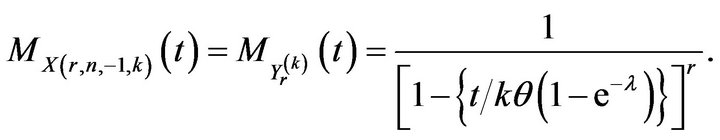 (16)
(16)
Differentiating 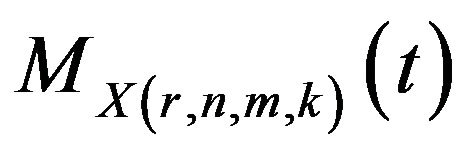 with respect to t and evaluating at
with respect to t and evaluating at , we get the mean of the r-th
, we get the mean of the r-th  when
when 
 (17)
(17)
and when  that
that
 (18)
(18)
as obtained by [12] for exponential distribution at .
.
Special Cases
1) Putting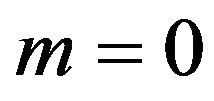 ,
,  in (11) and (17), the explicit formula for marginal moment generating function and mean of order statistics from Erlang-truncated exponential distribution can be obtained as
in (11) and (17), the explicit formula for marginal moment generating function and mean of order statistics from Erlang-truncated exponential distribution can be obtained as

and
 where
where
 .
.
2) Setting  in (16) and (18), the results for upper records from Erlang-truncated exponential distribution may be obtained in the form
in (16) and (18), the results for upper records from Erlang-truncated exponential distribution may be obtained in the form

and

as obtained by [13] for exponential distribution at  .
.
A recurrence relation for marginal moment generating function for  from
from  (1) can be obtained in the following theorem.
(1) can be obtained in the following theorem.
Theorem 2.1 For the distribution given in (1) and for 
 (19)
(19)
Proof [10] has shown that for a positive integer ,
,
 (20)
(20)
On substituting for  from (6) in (20) and simplifying the resulting expression, we find that
from (6) in (20) and simplifying the resulting expression, we find that
 (21)
(21)
Differentiating both the sides of (21) j times with respect to t, we get
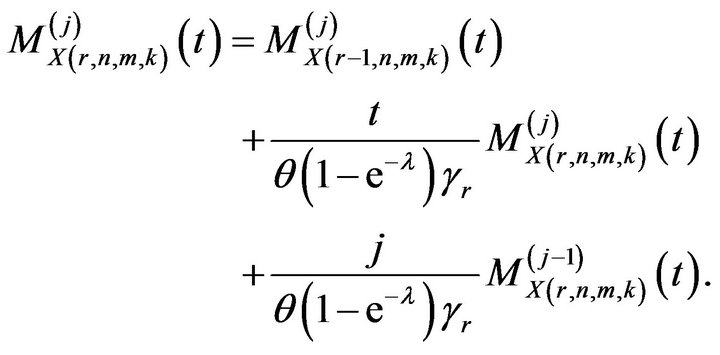
The recurrence relation in (19) is derived simply by rewriting the above equation.
At  in (19), we obtain the recurrence relations for moments of
in (19), we obtain the recurrence relations for moments of  from Erlang-truncated exponential distribution in the form
from Erlang-truncated exponential distribution in the form
 (22)
(22)
Remark 2.1 Putting ,
,  in (19) and (22), we can get the relations for marginal moment generating function and moments of order statistics for Erlang-truncated exponential distribution as
in (19) and (22), we can get the relations for marginal moment generating function and moments of order statistics for Erlang-truncated exponential distribution as

and

Remark 2.2 Setting  and
and  in (19) and (22), relations for record values can be obtained as
in (19) and (22), relations for record values can be obtained as
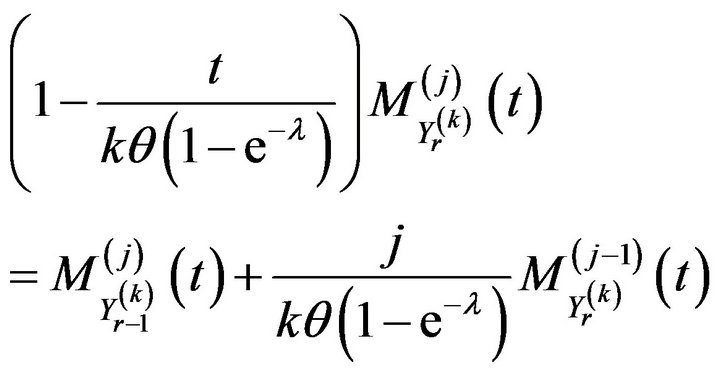
and

for 

Remark 2.3 At ,
,  in (22), the result for single moments of gos obtained by [2] for exponential distribution is deduced.
in (22), the result for single moments of gos obtained by [2] for exponential distribution is deduced.
3. Relations for Joint Moment Generating Functions
Before coming to the main results we shall prove the following Lemmas.
Lemma 3.1 For the Erlang-truncated exponential distribution as given in (1) and non-negative integers a, b and c with ,
,
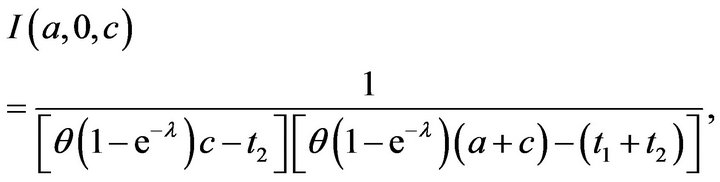 (23)
(23)
where
 (24)
(24)
Proof From (24), we have
 , (25)
, (25)
where
 . (26)
. (26)
On substituting for 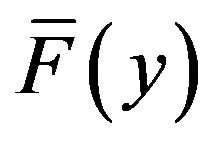 from (2) in (26), we get
from (2) in (26), we get
 .
.
Upon substituting this expression for  in (25) and then integrating the resulting expression, we establish the result given in (23).
in (25) and then integrating the resulting expression, we establish the result given in (23).
Lemma 3.2 For the distribution as given in (1) and any non-negative integers a, b and c,
 (27)
(27)
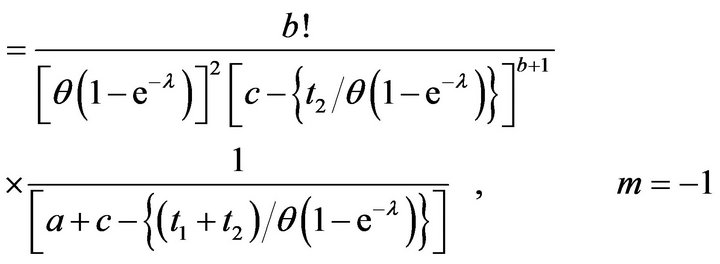 (28)
(28)
where  is as given in (24).
is as given in (24).
Proof Expanding  binomially in (24) after noting that
binomially in (24) after noting that
 , we get
, we get

Making use of Lemma 3.1, we establish the result given in (27).
When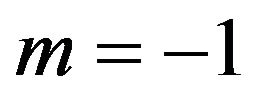 ,
,  as
as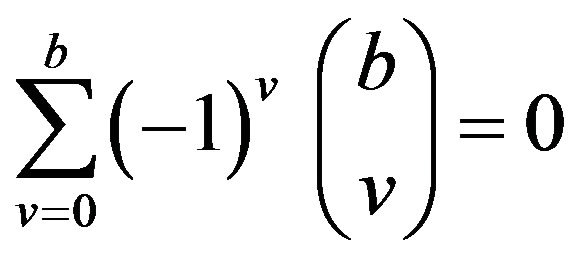 so after applying L’Hospital rule and (15), (28) can be proved on the lines of (16).
so after applying L’Hospital rule and (15), (28) can be proved on the lines of (16).
Theorem 3.1 For Erlang-truncated exponential distribution as given in (1) and for 
 (29)
(29)
 (30)
(30)
Proof From (5), we have
 (31)
(31)
upon using the relation (6). Now expanding  binomially in (31), we get
binomially in (31), we get

Making use of Lemma 3.2, we establish the relation given in (30).
Special Cases
1) Putting ,
,  in (30), the explicit formula for the joint moment generating function of order statistics of the Erlang-truncated exponential distribution can be obtained as
in (30), the explicit formula for the joint moment generating function of order statistics of the Erlang-truncated exponential distribution can be obtained as

where
 .
.
2) Putting  in (30), we deduce the explicit expression for joint moment generating function of upper k record values for Erlang-truncated exponential distribution in view of (29) and (28) in the form
in (30), we deduce the explicit expression for joint moment generating function of upper k record values for Erlang-truncated exponential distribution in view of (29) and (28) in the form
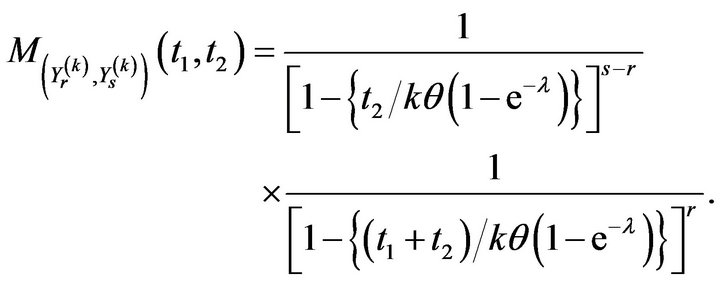
Differentiating  and evaluating at
and evaluating at , we get the product moments of
, we get the product moments of  when
when 
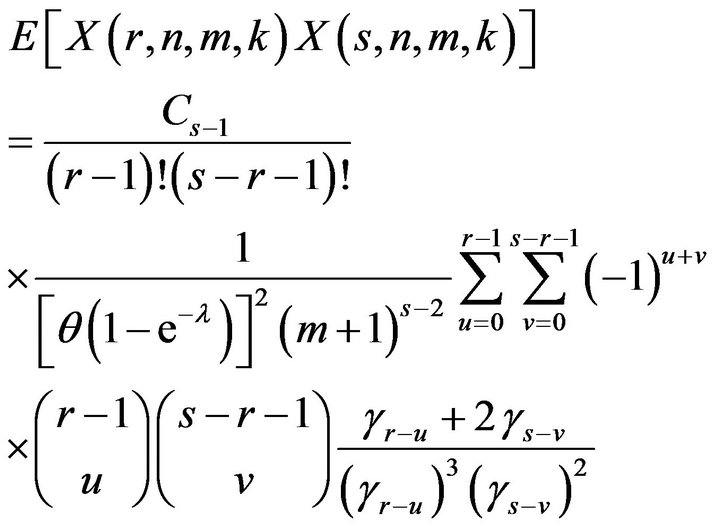 (32)
(32)
and when  that
that
 (33)
(33)
and for 
 .
.
Making use of (6), we can derive the recurrence relations for joint moment generating function of  from (5).
from (5).
Theorem 3.2 For the distribution given in (1) and for 
 (34)
(34)
Proof [10] has shown that for 
 and a fixed positive integer
and a fixed positive integer 

Differentiating both the sides of (34)  times with respect to
times with respect to 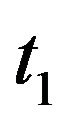 and then
and then  times with respect to
times with respect to , we get
, we get

which, when rewritten gives the recurrence relation in (26).
At 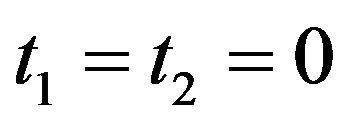 in (34), we obtain the recurrence relations for product moments of gos from Erlang-truncated exponential distribution in the form
in (34), we obtain the recurrence relations for product moments of gos from Erlang-truncated exponential distribution in the form
 (35)
(35)
One can also note that Theorem 2.1 can be deduced from Theorem 3.2 by letting 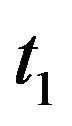 tends to zero.
tends to zero.
Remark 3.1 Putting ,
,  in (34) and (35), we obtain the recurrence relations for joint moment generating function and product moments of order statistics for Erlang-truncated exponential distribution in the form
in (34) and (35), we obtain the recurrence relations for joint moment generating function and product moments of order statistics for Erlang-truncated exponential distribution in the form
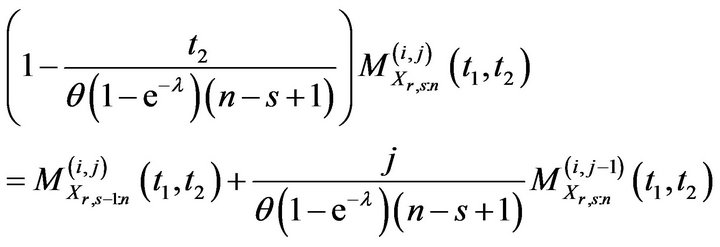
and

as obtained by [14] for exponential distribution at  and
and .
.
Remark 3.2 Substituting  and
and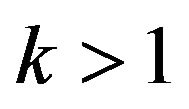 , in (34) and (35), we get recurrence relations for joint moment generating function and product moments of upper k record values for Erlang-truncated exponential distribution.
, in (34) and (35), we get recurrence relations for joint moment generating function and product moments of upper k record values for Erlang-truncated exponential distribution.
4. Characterization
Let  be
be , then the conditional
, then the conditional  of
of  given
given 
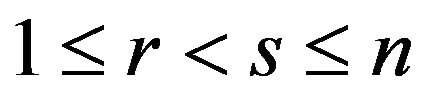 , in view of (4) and (5), is
, in view of (4) and (5), is
 (36)
(36)
Theorem 4.1 Suppose , for all
, for all  be a distribution function of the random variable X and
be a distribution function of the random variable X and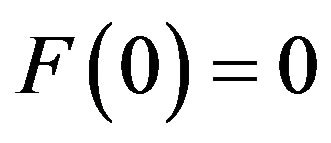 ,
, 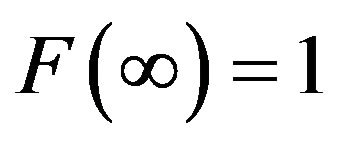 , then
, then
 (37)
(37)
if and only if
 .
.
Proof From (36), we have
 (38)
(38)
By setting  from (2) in (38)we obtain
from (2) in (38)we obtain
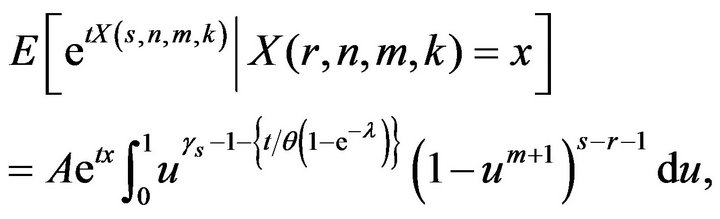 (39)
(39)
where
 .
.
Again by setting 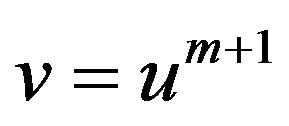 in (39), we get
in (39), we get

and hence the relation given in (37).
To prove sufficient part, we have from (36) and (37)
 (40)
(40)
where
 .
.
Differentiating (40) both the sides with respect to , we get
, we get

or
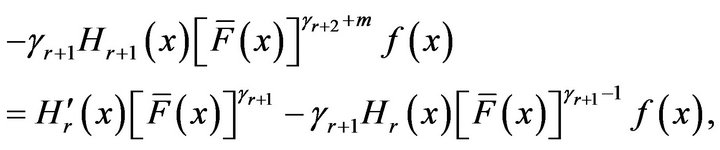
where
 and
and

Therefore,

which proves that