Approximate Solution of Fuzzy Matrix Equations with LR Fuzzy Numbers ()
1. Introduction
Systems of simultaneous matrix equations are essential mathematical tools in science and technology. In many applications, at least some of the parameters of the system are represented by fuzzy rather than crisp numbers. So, it is very important to develop a numerical procedure that would appropriately handle and solve fuzzy matrix systems. The concept of fuzzy numbers and arithmetic operations were first introduced and investigated by Zadeh [1] and Dubois [2].
Since M. Friedman et al. [3] proposed a general model for solving a n × n fuzzy linear systems whose coefficients matrix is crisp and the right-hand side is a fuzzy number vector in 1998, many works have been done about how to deal with some advanced fuzzy linear systems such as dual fuzzy linear systems (DFLS), general fuzzy linear systems (GFLS), fully fuzzy linear systems (FFLS), dual fully fuzzy linear systems (DFFLS) and general dual fuzzy linear systems (GDFLS), see [4-9]. However, for a fuzzy linear matrix equation which always has a wide use in control theory and control engineering, few works have been done in the past decades. In 2010, Gong Zt [10,11] investigated a class of fuzzy matrix equations 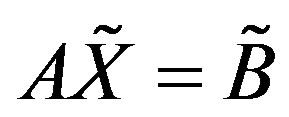 by means of the undetermined coefficients method, and studied least squares solutions of the inconsistent fuzzy matrix equation by using generalized inverses. In 2011, Guo X. B. [12] studied the minimal fuzzy solution of fuzzy Sylvester matrix equations
by means of the undetermined coefficients method, and studied least squares solutions of the inconsistent fuzzy matrix equation by using generalized inverses. In 2011, Guo X. B. [12] studied the minimal fuzzy solution of fuzzy Sylvester matrix equations . Recently, they [13] considered the fuzzy symmetric solutions of fuzzy matrix equations
. Recently, they [13] considered the fuzzy symmetric solutions of fuzzy matrix equations .
.
The LR fuzzy number and its operations were firstly introduced by Dubois [2]. In 2006, Dehgham et al. [6] discussed the computational methods for fully fuzzy linear systems whose coefficient matrix and the right-hand side vector are denoted by LR fuzzy numbers. In this paper, we propose a practical method for solving a class of fuzzy matrix system  in which A is an m × n crisp matrix and
in which A is an m × n crisp matrix and 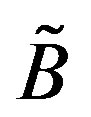 is an m × p arbitrary LR fuzzy numbers matrix. In contrast, the contribution of this paper is to generalize Dubois’ definition and arithmetic operation of LR fuzzy numbers and then use this result to solve fuzzy matrix systems numerically. The importance of converting fuzzy linear system into two systems of linear equations is that any numerical approach suitable for system of linear equations may be implemented. In addition, since our model does not contain parameter r,
is an m × p arbitrary LR fuzzy numbers matrix. In contrast, the contribution of this paper is to generalize Dubois’ definition and arithmetic operation of LR fuzzy numbers and then use this result to solve fuzzy matrix systems numerically. The importance of converting fuzzy linear system into two systems of linear equations is that any numerical approach suitable for system of linear equations may be implemented. In addition, since our model does not contain parameter r,  , its numerical computation is relatively easy.
, its numerical computation is relatively easy.
2. Preliminaries
Definition 2.1. [2] A fuzzy number  is said to be a LR fuzzy number if
is said to be a LR fuzzy number if

where m is the mean value of , and
, and 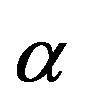 and
and are left and right spreads, respectively. The function
are left and right spreads, respectively. The function , which is called left shape function satisfying: 1)
, which is called left shape function satisfying: 1)
 ; 2)
; 2)  and
and ; 3)
; 3)  is a non increasing on
is a non increasing on .
.
The definition of a right shape function is usually similar to that of
is usually similar to that of . A LR fuzzy number
. A LR fuzzy number is symbolically shown as
is symbolically shown as .
.
Noticing that 
 in Definition 2.1, which limits its applications, we extend the definition of LR fuzzy numbers as follows.
in Definition 2.1, which limits its applications, we extend the definition of LR fuzzy numbers as follows.
Definition 2.2. (Generalized LR fuzzy numbers) Let , we define
, we define
1) if 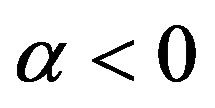 and
and , then
, then
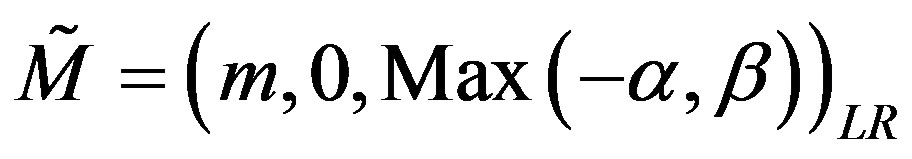 , and
, and
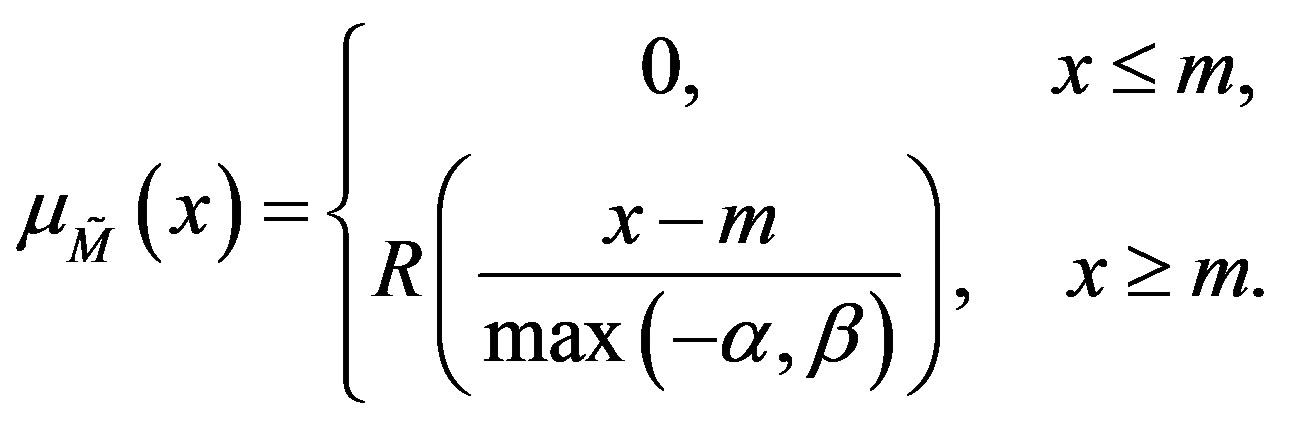
2) if  and
and , then
, then
 , and
, and

3) if  and
and , then
, then , and
, and

For arbitrary LR fuzzy number  and
and , we have
, we have
1) 
2) 
Definition 2.3. The matrix system
 (1)
(1)
where  are crisp numbers and
are crisp numbers and  are LR fuzzy numbers, is called a LR fuzzy matrix equation (LRFME).
are LR fuzzy numbers, is called a LR fuzzy matrix equation (LRFME).
Using matrix notation, we have
 . (2)
. (2)
A LR fuzzy numbers matrix
 ,
,  ,
,
 ,
, 
is called a solution of the LR fuzzy matrix systems if  satisfies (2).
satisfies (2).
3. Method for Solving LRFME
In this section we investigate the LR fuzzy matrix system (2). Firstly, we propose a model for solving the LR fuzzy matrix system, i.e., convert it into two crisp systems of matrix equations. Then we define the LR fuzzy solution and give its solution representation to the original fuzzy matrix system. At last, the existence condition of the strong LR fuzzy solution to the original fuzzy matrix system is also discussed.
3.1. Extended Crisp Matrix Equations
By using arithmetic operations of LR fuzzy numbers, we extend the LR fuzzy matrix Equation (2) into two crisp matrix equations.
Theorem 3.1. The LR dual fuzzy linear Equation (2) can be extended into two crisp systems of linear equations as follows:
 , (3)
, (3)
i.e.,

and
 , (4)
, (4)
i.e.,

where 
 ,
,  are determined as follows:
are determined as follows:
If , then
, then ,
,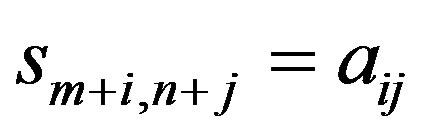 ; if
; if , then
, then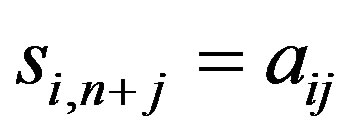 ,
,  , and any
, and any  which is not determined by the above items is zero,
which is not determined by the above items is zero,  ,
, .
.
Proof. Let 

and 
 .
.
Then the fuzzy matrix Equation (1) can be rewritten in the block forms
 Thus the original system (1) is equivalent to the following fuzzy linear equations
Thus the original system (1) is equivalent to the following fuzzy linear equations
 (5)
(5)
Now we consider the Equations (4). Let  be the ith row of matrix A,
be the ith row of matrix A, 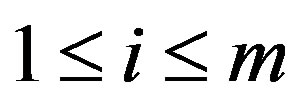 , we can represent
, we can represent  in the form
in the form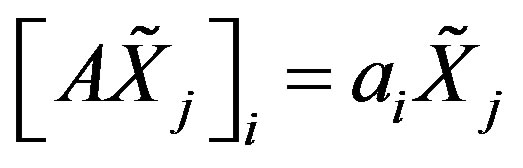 ,
, .
.
Denoting  and
and
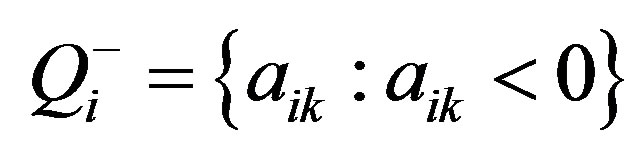 , we have
, we have
 .
.
i.e.,
 (6)
(6)
Consider the given LR fuzzy vector
 we can write the system (2) as
we can write the system (2) as

Suppose the system ,
,  has a solution. Then, the corresponding mean value
has a solution. Then, the corresponding mean value
 of the solution must lie in the following linear system
of the solution must lie in the following linear system
 . (7)
. (7)
Meanwhile, the left spread 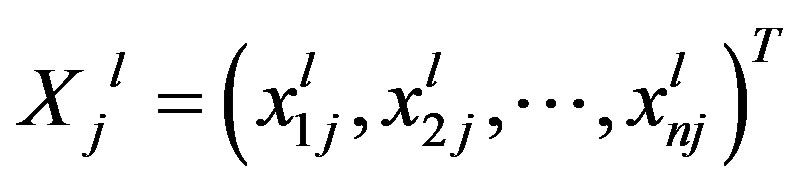 and the right spread
and the right spread  of the solution can be derived from solving the following crisp linear system
of the solution can be derived from solving the following crisp linear system
 . (8)
. (8)
Finally, we restore the Equation (5) and obtain above matrix Equations (3) and (4).
The proof is completed.
3.2. Computing Model Matrix Equations
In order to solve the original fuzzy linear Equation (2), we need to consider crisp matrix Equations (3) and (4). Since Equations (3) and (4) are crisp, their computation is relatively easy.
In general [14], the minimal solutions of matrix systems (3) and (4) can be expressed uniformly by
 (9)
(9)
and
 (10)
(10)
respectively, no matter the Equations (3) and (4) are consistent or not.
It seems that we have obtained the solution of the original fuzzy linear system (2) as follows:
 (11)
(11)
But the solution vector may still not be an appropriate LR fuzzy numbers vector except for . So we give the definition of the minimal LR fuzzy solution to the Equation (2) as follows:
. So we give the definition of the minimal LR fuzzy solution to the Equation (2) as follows:
Definition 3.1. Let 
 . If
. If  is the minimal solution of Equation (3),
is the minimal solution of Equation (3),  and
and  are minimal solution of Equation (4) such that
are minimal solution of Equation (4) such that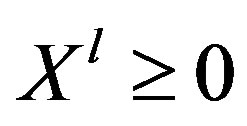 ,
,  , then we call
, then we call  is a strong LR fuzzy solution of Equation (2). Otherwise, it is a weak LR fuzzy solution of Equation (2) given by
is a strong LR fuzzy solution of Equation (2). Otherwise, it is a weak LR fuzzy solution of Equation (2) given by
 (12)
(12)
3.3. A Sufficient Condition of Strong Fuzzy Solution
The key points to make the solution vector being a LR fuzzy solution are  and
and . Since
. Since
 ,
,  we know that the non negativities of
we know that the non negativities of  and
and  are equivalent to the condition
are equivalent to the condition  now that
now that  is known.
is known.
By the above analysis, we have the following result.
Theorem 3.2. Let A belong to . If
. If  is nonnegative, the solution of the LR fuzzy matrix system (2) is expressed by
is nonnegative, the solution of the LR fuzzy matrix system (2) is expressed by
 (13)
(13)
and it admits a strong minimal LR fuzzy solution.
The following Theorem gives a result for such  to be nonnegative.
to be nonnegative.
Theorem 3.3. [15] Let S be an 2p × 2p nonnegative matrix with rank r. Then the following assertions are equivalent:
1)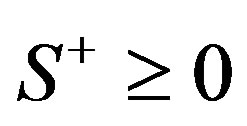 ;
;
2) There exists a permutation matrix P, such that PS has the form
 where each
where each  has rank 1 and the rows of
has rank 1 and the rows of  are orthogonal to the rows of
are orthogonal to the rows of , whenever
, whenever , the zero matrix may be absent.
, the zero matrix may be absent.
3) 
for some positive diagonal matrix . In this case,
. In this case,
 .
.
4. Numerical Examples
In this section, we work out two numerical examples to illustrate the proposed method.
Example 4.1. Consider the fuzzy matrix systems:
 .
.
The coefficient matrix A is nonsingular and the extended matrix S is singular. By the Theorem 3.1., the mean value x, the left spread  and the right spread
and the right spread 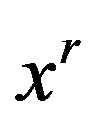 of solution are obtained from
of solution are obtained from
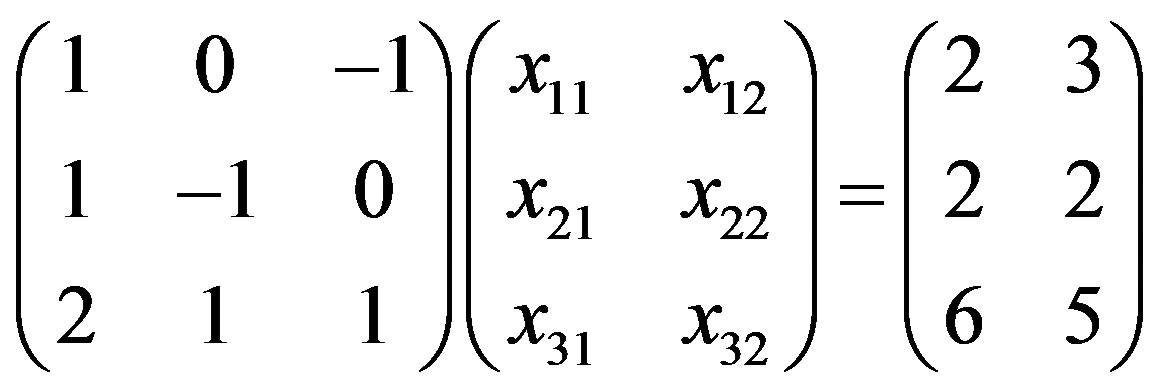
and
 .
.
Thus, we have

and
 .
.
Since  is negative, according to Definition 3.1., the LR fuzzy approximate solution of the original fuzzy matrix system is
is negative, according to Definition 3.1., the LR fuzzy approximate solution of the original fuzzy matrix system is

and it admits a strong LR fuzzy solution.
Example 4.2. Consider the following matrix systems:
 .
.
By the Theorem 3.1., the mean value x of solution lies in the following crisp matrix system
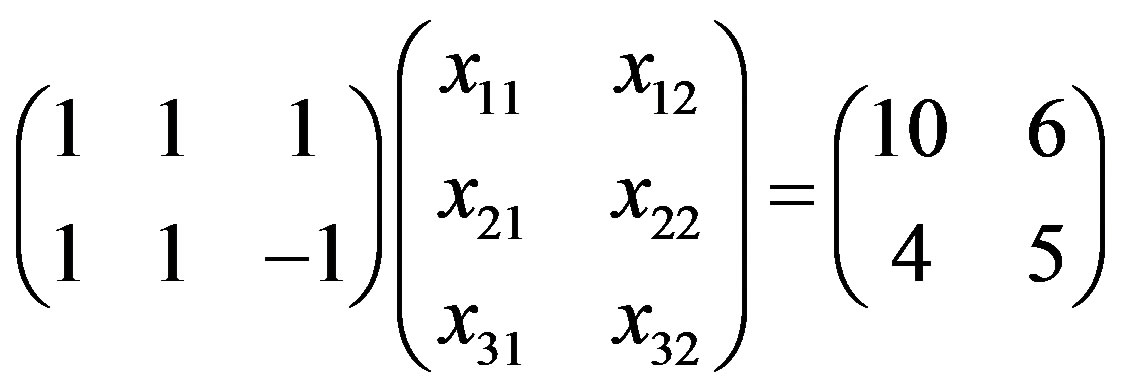 .
.
Meanwhile, the left spread  and the right spread
and the right spread  of solution are obtained by solving the following crisp matrix system
of solution are obtained by solving the following crisp matrix system
 .
.
Thus, we have

and

By Definition 3.1., the original fuzzy system has a strong LR fuzzy approximate solution given by
 .
.
5. Conclusion
In this work we proposed a general model for solving the fuzzy matrix equation 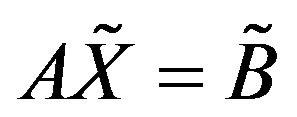 where A is an m × n crisp matrix and
where A is an m × n crisp matrix and  is a n × p arbitrary LR fuzzy numbers matrix. We converted the fuzzy matrix system into two crisp matrix equations and obtained the LR fuzzy solution to the original fuzzy system by solving crisp matrix equations. Moreover, the existence condition of strong LR fuzzy solution was studied. Numerical examples showed that our method is effective to solve LR fuzzy matrix equations.
is a n × p arbitrary LR fuzzy numbers matrix. We converted the fuzzy matrix system into two crisp matrix equations and obtained the LR fuzzy solution to the original fuzzy system by solving crisp matrix equations. Moreover, the existence condition of strong LR fuzzy solution was studied. Numerical examples showed that our method is effective to solve LR fuzzy matrix equations.
6. Acknowledgements
The authors are very thankful for the reviewer’s helpful suggestions to improve the paper. This research was financially supported by the National Natural Science Foundation of China (Grant No. 71061013) and the Youth Scientific Research Ability Promotion Project of Northwest Normal University (NWNU-LKQN-11-20).