On the Generality of Orthogonal Projections and e-Projections in Banach Algebras ()
1. Introduction
Orthogonal projections on Hilbert spaces play important roles in many applications in mathematics, science and engineering including signal and image processing, integral equations and many other areas. In this article we introduce generalized orthogonal projections, generalized e-projections in Banach algebras and we show that they share many useful properties with their corresponding notions in C*-algebras. For more information we refer to the articles by Berkson [1], Schmoeger [2], Du et al. [3], Grob et al. [4] and Lebtahi et al. [5].
The paper is organized as follows: Section 1, contains a few elementary definitions and results from Banach algebras theory. In this section we introduce the concepts of numerical range and the spectrum and the spectral radius of an element and investigate their properties. In section 2, we introduce the generalized orthogonal projections, generalized e-projections in Banach algebras and we study some necessary and sufficient conditions for them and their spectrums.
Throughout this paper,  will denote a complex unital Banach algebras (with unit 1) and
will denote a complex unital Banach algebras (with unit 1) and  denote the dual space of
denote the dual space of  . For
. For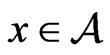
 ,
,  , define the support set at x
, define the support set at x
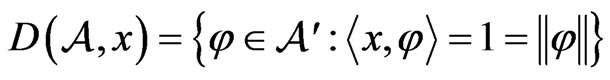
Then for all  define the sets
define the sets

and their union, the numerical range of 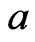
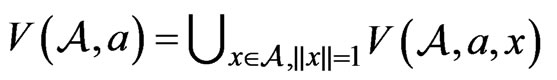
We also denote the spectrum and the spectral radius of 𝔞 by  and
and  respectively.
respectively.
Lemma 1.1. [6]. Let  then 1)
then 1) 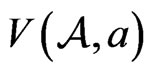 is a compact convex subset of ℂ.
is a compact convex subset of ℂ.
2) 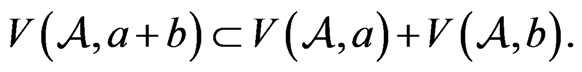
3) 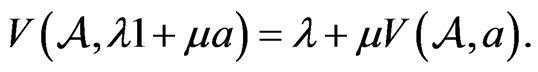
4) 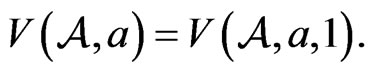
5) 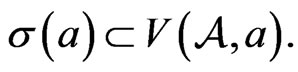
The fundamental link between the numerical range of  and the group
and the group  is as follows:
is as follows:
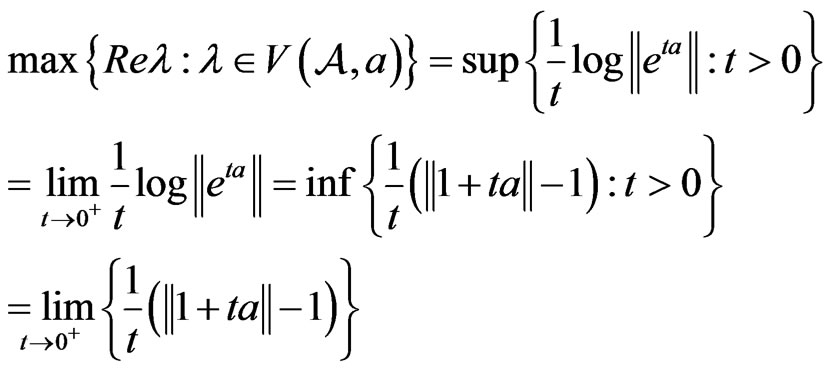
By Lemma 5.2 of [6], an element 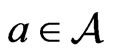 is said to be hermitian if
is said to be hermitian if  or equivalently
or equivalently 
 , equivalently
, equivalently .
.
We denote the set of all hermitian elements of  by
by . It is well-known that if
. It is well-known that if  then the convex hull of the spectrum satisfies
then the convex hull of the spectrum satisfies  and
and . Also
. Also  is closed real subspace of
is closed real subspace of  and
and  and if
and if  then
then 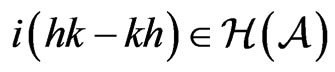
Furthermore, if  is a
is a  -algebra, then by Example 5.3 of [6],
-algebra, then by Example 5.3 of [6], 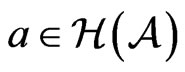 if and only if
if and only if .
.
An element  is called positive if
is called positive if  . We denote the set of all positive elements of
. We denote the set of all positive elements of  by
by . By Theorem 5.14 of [6],
. By Theorem 5.14 of [6],  if and only if
if and only if  and
and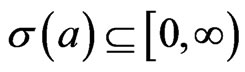 . In the real Banach space
. In the real Banach space , the set
, the set  is a normal closed cone in which 1 is an interior point. Let
is a normal closed cone in which 1 is an interior point. Let  . Since
. Since , hence each element of
, hence each element of 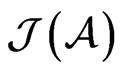 has a unique representation of the form
has a unique representation of the form  with
with . If we define a linear involution
. If we define a linear involution  from
from  to itself by
to itself by  then
then  with the norm of
with the norm of  is a complex Banach space and
is a complex Banach space and  is a continuous linear involution on
is a continuous linear involution on . In the general case
. In the general case 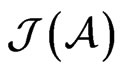 is not an algebra and
is not an algebra and  is not an involution because in particular
is not an involution because in particular 
 . However, if
. However, if  and for every
and for every 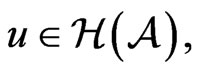
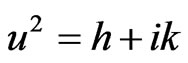 with
with ,
,  , then
, then  is a complex unital
is a complex unital  -algebra with continuous involution
-algebra with continuous involution  and
and  is its set of self-adjoint elements [6].
is its set of self-adjoint elements [6].
We say that  is normal if
is normal if 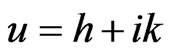 with
with 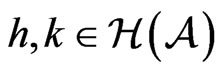 and
and . Observe that
. Observe that  is normal if and only if
is normal if and only if 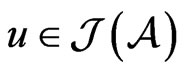 and
and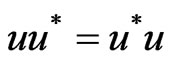 . An element
. An element  satisfying
satisfying  is called a partial isometry.
is called a partial isometry.
Definition 1.2. Let 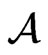 be a complex unital
be a complex unital  -algebra, then
-algebra, then 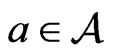 is called an orthogonal projection if
is called an orthogonal projection if . Moreover
. Moreover  is called a Moore-Penrose invertible if there exists some
is called a Moore-Penrose invertible if there exists some  such that
such that

In this case 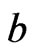 is the Moore-Penrose inverse of
is the Moore-Penrose inverse of  and usually denoted by
and usually denoted by . If
. If  is Moore-Penrose invertible, then
is Moore-Penrose invertible, then  is unique.
is unique.
Definition 1.3. Let  be a complex unital Banach algebra. An element
be a complex unital Banach algebra. An element  is called an orthogonal projection if
is called an orthogonal projection if  and
and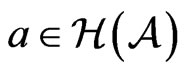 . Moreover
. Moreover 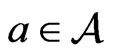 is called a Moore-Penrose invertible if there exists
is called a Moore-Penrose invertible if there exists  such that
such that

then the element  is called the Moore-Penrose inverse of
is called the Moore-Penrose inverse of , and it also will be denoted by
, and it also will be denoted by . The MoorePenrose inverse of
. The MoorePenrose inverse of  is unique in the case when it exists.
is unique in the case when it exists.
If 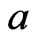 is Moore-Penrose invertible then the equality
is Moore-Penrose invertible then the equality  does not hold in general. Hence it is interesting to distinguish such elements.
does not hold in general. Hence it is interesting to distinguish such elements.
Definition 1.4. An element  of a unital Banach algebra
of a unital Banach algebra  is said to be e-projection if there exists
is said to be e-projection if there exists  and
and .
.
If 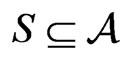 , we define the centralizer of
, we define the centralizer of 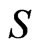 by
by
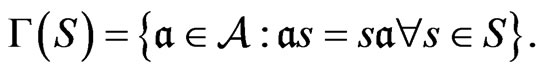
We say that  commutes if any two elements of
commutes if any two elements of  commute with each other. If
commute with each other. If  is commutes and
is commutes and  then by Theorem 11.22 of [7]
then by Theorem 11.22 of [7]  is a commutative Banach algebra (with unit 1),
is a commutative Banach algebra (with unit 1),  and
and  for every
for every .
.
Lemma 1.5. [7]. Let  be a complex unital Banach algebra, let
be a complex unital Banach algebra, let  be a normal element,
be a normal element, . If
. If 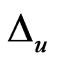 is the set of all nontrivial complex homomorphisms of
is the set of all nontrivial complex homomorphisms of . Then 1)
. Then 1) 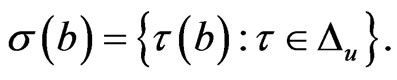
2) 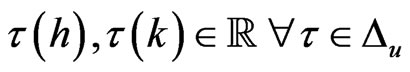
3)  for all
for all  and
and 
4) If , then
, then
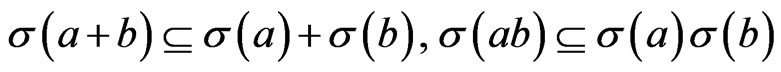
2. g-Orthogonal Projections and Generalized e-Projections
Definition 2.1. An element  is called generalized orthogonal projection or simply a g-orthogonal projection if there exists a natural number
is called generalized orthogonal projection or simply a g-orthogonal projection if there exists a natural number  such that
such that  Also
Also  is said to be generalized e-projection if there exists
is said to be generalized e-projection if there exists  and
and 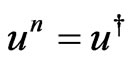
Theorem 2.2. Suppose that  is a g-orthogonal projection. Then 1)
is a g-orthogonal projection. Then 1)  is normal.
is normal.
2) 
3) If  for all
for all  then
then
 and
and 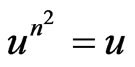
Proof.
1) Since  hence we have
hence we have
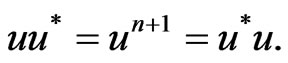
2) Let , then by the Lemma 1.5 there is a
, then by the Lemma 1.5 there is a  such that
such that , thus we have
, thus we have
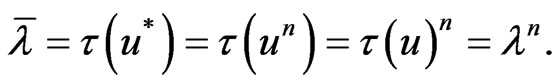
Now if , then
, then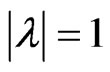 and hence
and hence 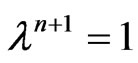 which implies that
which implies that 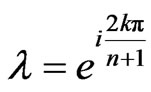 with
with 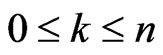
3) Since  hence
hence
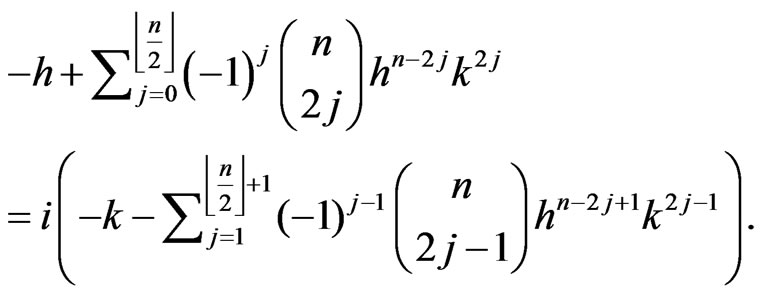
Using the Lemma 1.6 (4) we have
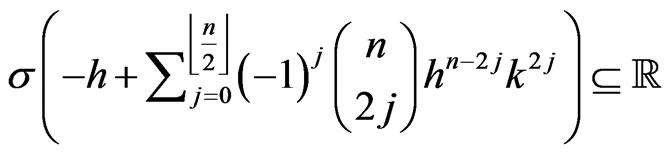
and

This yields
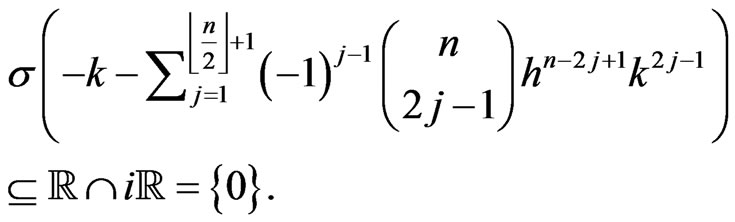
Thus we have

Since
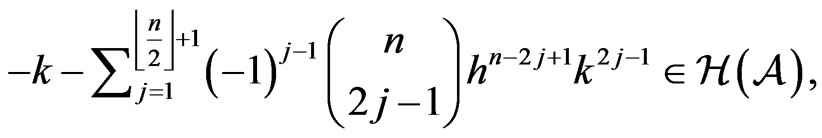
hence
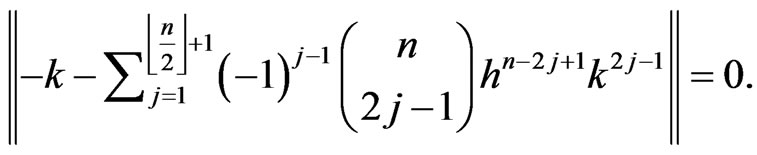
which shows that
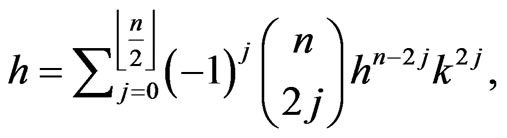
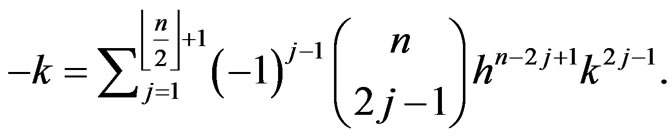
Therefore
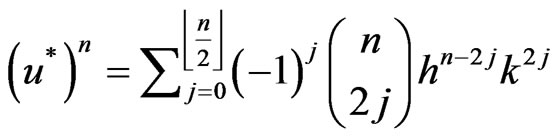
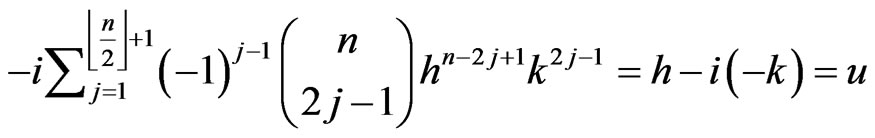
The second implication is obvious.
Theorem 2.3. Let  be a generalized e-projection. Then 1)
be a generalized e-projection. Then 1) 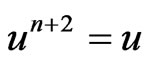 and
and  is an e-projection.
is an e-projection.
2) 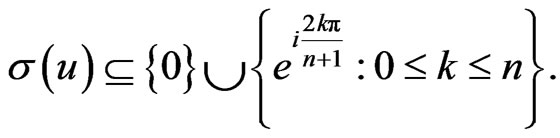
Proof.
1) Since  hence we have
hence we have 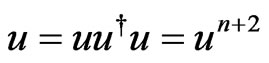 and
and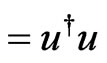
 .
.
2) This follows immediately from Theorem 2.2.
Theorem 2.4. Let  and
and
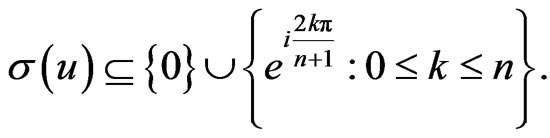
Then the following statements hold:
1) If  is normal, then
is normal, then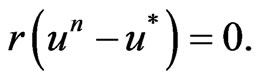
2) If  for all
for all , then
, then  is a g-orthogonal projection.
is a g-orthogonal projection.
Proof.
1) Put 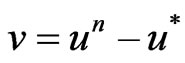 Since
Since  is normal hence
is normal hence  and so
and so  Now suppose that
Now suppose that , then there exists some
, then there exists some  with
with .
.
Let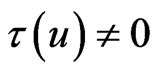 , since
, since  thus
thus
 . This shows that
. This shows that  , and so
, and so  From this we have
From this we have .
.
2) By the Murphy’s Theorem [8],  so
so  is normal. Now from
is normal. Now from  we obtain
we obtain

Using the Lemma 1.6(4) and applying (1) we have
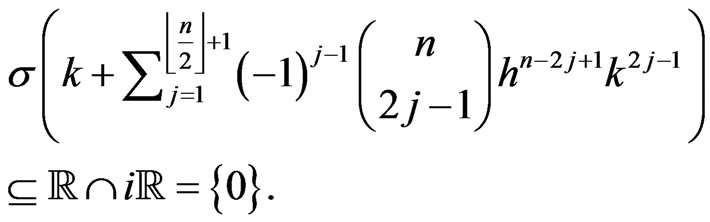
Since  for all
for all , hence
, hence
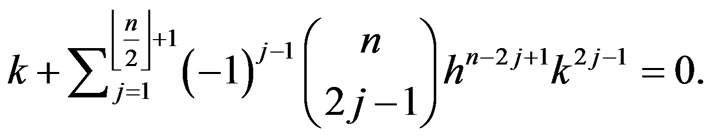
This shows that
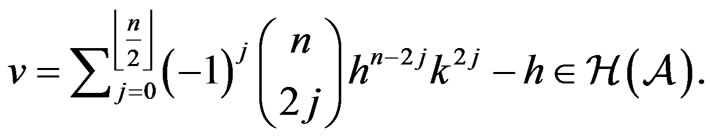
Since , thus
, thus , which implies that
, which implies that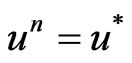 .
.
Theorem 2.5. An element  is a g-orthogonal projection if and only if u is normal and
is a g-orthogonal projection if and only if u is normal and
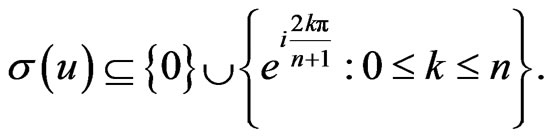
Proof. If u is a g-orthogonal projection then the implication follows from the Theorem 2.2. Conversely suppose that u is normal and
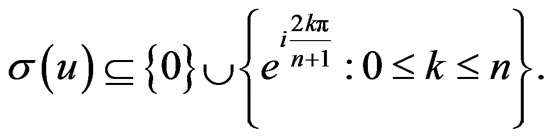
For every 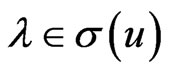 we define the Reiesz projection of u associated with
we define the Reiesz projection of u associated with 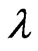 by
by 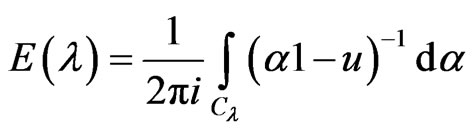
where  is a smooth closed curve which
is a smooth closed curve which  interior to
interior to  and
and  exterior to
exterior to . Then by Proposition VII.4.11 of [9], u has the representation as folslows:
. Then by Proposition VII.4.11 of [9], u has the representation as folslows:

where  for all
for all

and 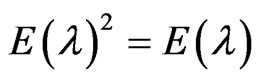 and
and
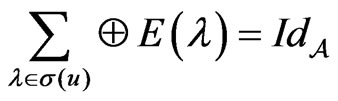
and  for
for 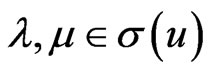 and
and  . Now we compute
. Now we compute
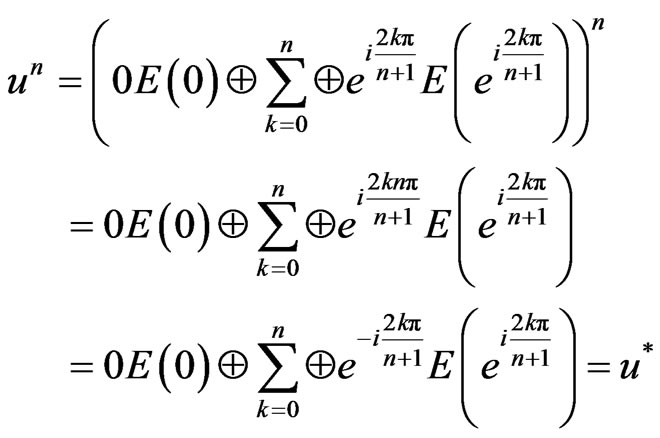
Theorem 2.6. Suppose that  and
and
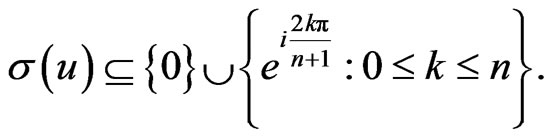
If u has the representation

where

is a Riesz projection of u associated with  and
and  is a smooth closed curve which
is a smooth closed curve which  interior to
interior to  and
and 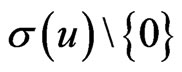 exterior to
exterior to . Then u is a generalized eprojection.
. Then u is a generalized eprojection.
Proof. Since for all 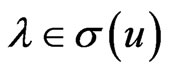 we have
we have  hence
hence
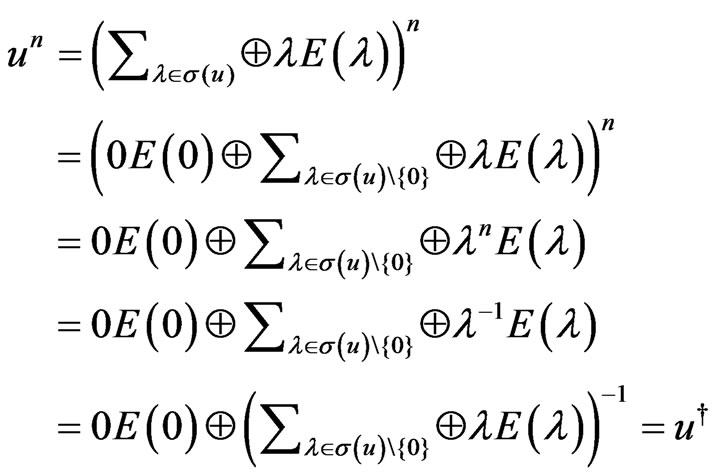
In the general case if  then it does not follows that
then it does not follows that .
.
Example 2.7. Let  with pointwise multiplication and let
with pointwise multiplication and let  be defined by
be defined by
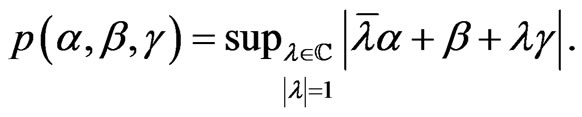
Define the norm  on
on  by
by

Then  is a complex commutative Banach algebra with unit
is a complex commutative Banach algebra with unit  If
If  then the following properties are shown in [6].
then the following properties are shown in [6].
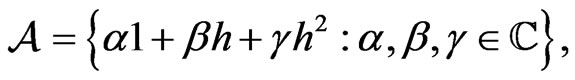
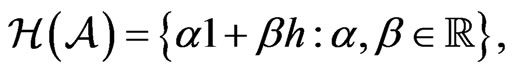
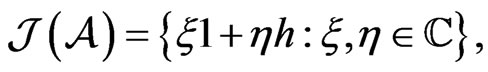
and  but
but  and each element of
and each element of  is normal. Furthermore if
is normal. Furthermore if , then
, then 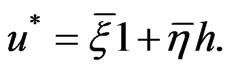
Lemma 2.8. Let  as in Example 2.7. Then
as in Example 2.7. Then  is a g-orthogonal projection if and only if
is a g-orthogonal projection if and only if
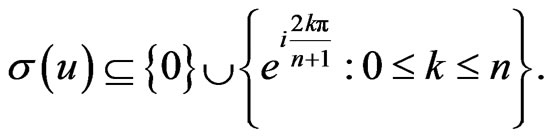
Proof. For all  we have
we have

hence 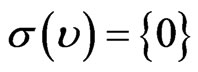 if and only if
if and only if  Now if
Now if
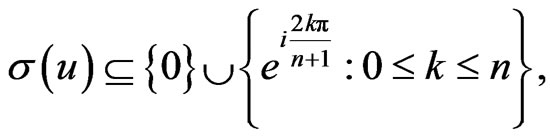
then by Theorem 2.4, we have  which implies that
which implies that . The converse implication follows immediately from Theorem 2.2.
. The converse implication follows immediately from Theorem 2.2.
Lemma 2.9. Let  as in Example 2.7 and
as in Example 2.7 and . Then the following conditions are equivalent:
. Then the following conditions are equivalent:
1) 
2) 
3) 
4) 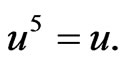
Proof.
1)  2) follows from the Lemma 2.8.
2) follows from the Lemma 2.8.
2)  3) Let
3) Let  Since
Since  hence
hence
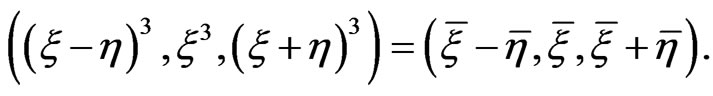
If  then
then  thus
thus  with
with 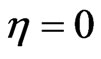 or
or  Let
Let 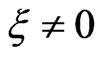 Since
Since  hence
hence  and
and  It follows
It follows  therefore
therefore 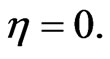 This shows that
This shows that  with
with .
.
(3)  (4): Clear.
(4): Clear.
(4)  (1): follows from the spectral mapping theorem.
(1): follows from the spectral mapping theorem.
Theorem 2.10. Let  be g-orthogonal projections such that
be g-orthogonal projections such that . Then
. Then  is a g-orthogonal projection.
is a g-orthogonal projection.
Proof. By the hypotheses
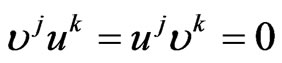
for all  hence we have
hence we have

3. Acknowledgements
The author expresses his gratitude to the referee for carefully reading of the manuscript and giving useful comments.